Эффективность и требования робастности могут часто описываться в терминах усиления ответа разомкнутого контура. Например, высокое усиление в низких частотах уменьшает установившиеся смещения и улучшает подавление помех. Точно так же высокочастотный спад улучшает устойчивость, где модель объекта управления сомнительна или неточна. Loop shaping является подходом к системе управления, в которой вы определяете подходящий профиль для отклика системы разомкнутого контура и проектируете контроллер, чтобы достигнуть той формы.
Неопределенность в вашей модели объекта управления может быть ограничивающим фактором в определении, чего можно достигнуть с обратной связью. Высокие усиления цикла могут ослабить эффекты неопределенности модели объекта управления и уменьшать полную чувствительность системы к воздействиям. Но если ваша неопределенность модели объекта управления является столь большой, что вы даже не знаете знак своего усиления объекта, затем вы не можете использовать большие усиления обратной связи без риска, что система станет нестабильной.
Поэтому большая часть проектирования контроллера включает компромисс между эффективностью и робастностью против неопределенности. Команды Robust Control Toolbox™ для формирующего цикл проектирования контроллера позволяют вам определить компромисс, который лучше всего удовлетворяет требования вашей системы.
loopsyn — Проектирует стабилизировавшийся контроллер, который формирует ответ разомкнутого контура, чтобы аппроксимировать целевую форму цикла, которую вы обеспечиваете. Можно настроить баланс между эффективностью и робастностью.
mixsyn — Проектирование контроллера оптимизировано для эффективности. Эта функция позволяет вам более точную спецификацию форм различных ответов цикла.
ncfsyn — Проектирование контроллера оптимизировано для робастности (запас устойчивости). Вы обеспечиваете функции взвешивания, которые формируют объект к желательному профилю.
Оптимизация эффективности mixsyn имеет тенденцию производить инвертирующие объект проекты, которые могут быть менее устойчивыми. В частности, mixsyn проекты могут быть хрупкими для плохо обусловленных объектов MIMO и для объектов со структурированной неопределенностью, такими как неопределенность на затухании и собственной частоте резонирующих режимов. В отличие от этого ncfsyn удерживает стратегии управления как инверсия объекта, которые используют точное знание объекта, подпирает шестами и обнуляет. Таким образом ncfsyn добавляет часть робастности к структурированной неопределенности, которая отсутствует в mixsyn проекты. Путем объединения элементов обоих ncfsyn и mixsyn, loopsyn подход может предоставить робастность и структурированной и неструктурированной неопределенности, также обеспечивая хорошую эффективность.
Вот некоторые компромиссы базовой конструкции, чтобы рассмотреть при выборе целевой формы цикла.
Устойчивая Устойчивость. Используйте целевую форму цикла с усилением максимально низко на высоких частотах, где обычно ваша модель объекта управления так плоха, что ее угол фазы абсолютно неточен с ошибками приближающиеся ±180 ° или больше.
Производительность. Используйте целевую форму цикла с усилением максимально высоко на частотах, где ваша модель хороша. Выполнение так гарантирует хорошее отслеживание уставки и хорошее затухание воздействия.
Перекрестное соединение и Спад. Используйте целевую форму цикла с ее частотой среза на 0 дБ ωc между вышеупомянутыми двумя частотными диапазонами. Убедитесь, что целевая форма цикла прокручивается прочь с наклоном между-20 дБ/десятилетие и-30 дБ/десятилетие около ωc. Этот спад помогает сохранить задержку фазы приблизительно между-130 ° и-90 ° около перекрестного соединения для хороших запасов по фазе.
Помните об этих принципах при выборе целевой формы цикла для loopsyn или формирующий фильтры для ncfsyn. Для получения дальнейшей информации о выборе функций взвешивания для mixsyn, смотрите, что Цикл Смешанной Чувствительности Формирует.
Другие факторы, которые могут влиять на ваш выбор формы цикла, являются нестабильными полюсами и нулями объекта, которые накладывают основные ограничения на вашу частоту среза на 0 дБ ωc (см. [1]). Например, ωc должен быть больше собственной частоты любого нестабильного полюса объекта, и меньший, чем собственная частота любого нестабильного нуля объекта.
Если вы не заботитесь, чтобы выбрать целевую форму цикла, которая соответствует этим основным ограничениям, то вы не можете достигнуть хороших результатов. Например, loopsyn вычислит оптимальный формирующий цикл контроллер K поскольку целевой цикл формирует Gd это не удовлетворяет это требование, но получившийся ответ L = G*K может иметь плохую подгонку к целевой форме цикла Gd, и следовательно может быть невозможно удовлетворить вашим целям эффективности.
Кроме того, потому что неопределенность объекта обычно увеличивается с частотой, существует предел на полосе пропускания, которой можно надежно достигнуть. Например, рассмотрите аппроксимированную модель G0 объекта SISO G. Можно описать неопределенность на этом объекте как мультипликативная неопределенность Δ M, такой что . Неопределенность ограничена на каждой частоте, | Δ M (jω) | ≤ β (ω), где β (ω) является процентом неопределенности модели. Как правило, β (ω) мал в низких частотах (точная модель) и увеличивается на высоких частотах (неточная модель). Частота, где β (ω) = 2 метки критический порог, вне которого существует недостаточная информация об объекте, чтобы надежно спроектировать контроллер обратной связи. С такой 200%-й неопределенностью модели модель не обеспечивает индикации относительно угла фазы истинного объекта, что означает, что единственный способ, которым можно надежно стабилизировать объект, состоит в том, чтобы гарантировать, что усиление цикла меньше 1. Допуская дополнительный фактор двух полей для ошибки, ваша полоса пропускания системы управления по существу ограничивается частотным диапазоном, по которому ваша мультипликативная неопределенность объекта Δ M имеет величину усиления | Δ M | <1.
Для более глубокого понимания отношения между формами цикла эффективность и робастность, считают многомерную систему управления с обратной связью показанной в следующем рисунке.
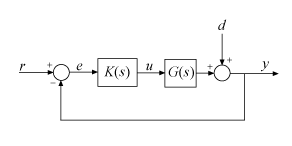
Чтобы определить количество многомерных запасов устойчивости и эффективности таких систем, можно использовать функцию чувствительности с обратной связью S и дополнительная функция чувствительности T, заданный как:
где L (s) является передаточной функцией разомкнутого контура
При определении целевой формы Gd (s) для передаточной функции разомкнутого контура L (s) эквивалентен внушительным ограничениям на сингулярные значения чувствительности S (s) и дополнительная чувствительность T (s). Например, для целевого цикла формируют с высоким усилением в низкой частоте, условии эквивалентно , где и обозначьте самые большие и самые маленькие сингулярные значения, соответственно. Точно так же для целевого цикла формируют с низким усилением на высокой частоте, эквивалентно .
При использовании loopsyn, вы задаете Gd (s) непосредственно, и loopsyn приблизительно налагает эти ограничения на чувствительность и дополнительную чувствительность. Для mixsyn, вы задаете функции взвешивания W 1 (s) и W 3 (s), таким образом, что W 1 (s) соответствует, 1/Gd (s) в низкой частоте меньше, чем 1 в другом месте, и W 3 (s) соответствия Gd (s) на высокой частоте и меньше, чем 1 в другом месте. (См., что Цикл Смешанной Чувствительности Формирует). То mixsyn приблизительно налагает ограничения и , которые примерно осуществляют форму цикла Gd.
Кроме того, робастность к мультипликативной неопределенности объекта эквивалентна наложению ограничения маленького усиления на T (s) (см. [1], p.342). Таким образом осуществление спада в цикле формирует Gd (или эквивалентно, ), обеспечивает некоторую робастность против несмоделированной динамики объекта на высокой частоте.
Для тех, кто более доволен классическими одноконтурными концепциями, существуют важные связи между мультипликативными запасами устойчивости, предсказанными усилением T (s) и предсказанные классическими M-кругами, как найдено на графике Николса. В случае SISO самое большое сингулярное значение T (s) является только пиковым усилением, данным:
Это количество является тем же количеством, которое вы получаете из M-кругов графика Николса. H ∞ норма (см. hinfnorm) многоконтурное обобщение резонансной пиковой величины с обратной связью, которая, как классические эксперты по управлению распознают, тесно связана с коэффициентом затухания доминирующих полюсов с обратной связью. Можно иметь отношение и к классическому запасу по амплитуде GM и запас по фазе θM в каждой обратной связи многомерной системы с обратной связью, проиллюстрированной выше, через формулы:
(См. [2].) Эти формулы допустимы обеспеченный и больше, чем 1, когда обычно имеет место. Поля применяются, даже когда возмущения усиления или возмущения фазы происходят одновременно в нескольких каналах обратной связи.
Нормы по бесконечности S и T также дают к допускам сокращения усиления. gM допуска сокращения усиления задан, чтобы быть минимальной суммой, которой должны были бы быть уменьшены усиления в каждом цикле для того, чтобы дестабилизировать систему. Верхние границы на gM следующие:
Для получения дополнительной информации об отношении между функциями чувствительности и запасами по амплитуде и фазе, см. [3].
[1] Skogestad, Сигерд, Иэн Постлетвэйт. Многомерное управление с обратной связью: анализ и проектирование. Чичестер; Нью-Йорк: Вайли, 1996.
[2] Lehtomaki, N., Н. Сэнделл и М. Атэнс. "Результаты робастности в Линейно-квадратичных Гауссовых Основанных Многомерных Системах управления". Транзакции IEEE на Автоматическом управлении 26, № 1 (февраля 1981):75–93.
[3] Seiler, Питер, Эндрю Пэкард и Паскаль Гахине. “Введение в Дисковые Поля [Примечания Лекции]”. Журнал 40 Систем управления IEEE, № 5 (октябрь 2020): 78–95.