Частота ошибок по битам (BER)

Теоретические результаты

Общее обозначение

Следующее обозначение используется в этом Приложении:

Количество или операция	Обозначение
Размер совокупности модуляции	$M$
Количество битов на символ	$k = {журнал}_{2} M$
Энергия на отношение спектральной плотности степени бита к шуму	$\frac{E_{b}}{N_{0}}$
Энергия на отношение спектральной плотности степени символа к шуму	$\frac{E_{s}}{N_{0}} = k \frac{E_{b}}{N_{0}}$
Частота ошибок по битам (BER)	$P_{b}$
Коэффициент ошибок символа (SER)	$P_{s}$
Действительная часть	$Ре [\cdot]$
Самое большое целое число, меньшее, чем	$⌊ \cdot ⌋$

Следующие математические функции используются:

Функция	Математическое выражение
Q функция	$Q (x) = \frac{1}{\sqrt{2 π}} \int_{x}^{\infty} \exp (- t^{2} / 2) d t$
Marcum Q функция	$Q (a, b) = \int_{b}^{\infty} t \exp (- \frac{t^{2} + a^{2}}{2}) I_{0} (a t) d t$
Измененная Функция Бесселя первого вида порядка $ν$	$I_{ν} (z) = \sum_{k = 0}^{\infty} \frac{{(z / 2)}^{υ + 2 k}}{k! Γ (ν + k + 1)}$ где $Γ (x) = \int_{0}^{\infty} e^{- t} t^{x - 1} d t$ гамма функция.
Вырожденная гипергеометрическая функция	${}_{1}F_{1} (a, c; x) = \sum_{k = 0}^{\infty} \frac{{(a)}_{k}}{{(c)}_{k}} \frac{x^{k}}{k!}$ где символ Pochhammer, ${(λ)}_{k}$ , задан как ${(λ)}_{0} = 1$ , ${(λ)}_{k} = λ (λ + 1) (λ + 2) \dots (λ + k - 1)$ .

Следующие акронимы используются:

Акроним	Определение
M-PSK	M-арное манипулирование сдвига фазы
DE-M-PSK	Дифференцированно закодированное M-арное манипулирование сдвига фазы
BPSK	Бинарное манипулирование сдвига фазы
DE-BPSK	Дифференцированно закодированное бинарное манипулирование сдвига фазы
QPSK	Четвертичное манипулирование сдвига фазы
DE-QPSK	Дифференцированно закодированное квадратурное манипулирование сдвига фазы
OQPSK	Сместите квадратурное манипулирование сдвига фазы
DE-OQPSK	Дифференцированно закодированное квадратурное манипулирование сдвига фазы смещения
M-DPSK	M-арное дифференциальное манипулирование сдвига фазы
M-PAM	M-арная импульсная амплитудная модуляция
M-QAM	M-арная квадратурная амплитудная модуляция
M-FSK	M-арное манипулирование сдвига частоты
MSK	Минимальное манипулирование сдвига
M-CPFSK	M-арное манипулирование сдвига частоты непрерывной фазы

Аналитические Выражения, Используемые в berawgn

M-PSK
DE-M-PSK
OQPSK
DE-OQPSK
M-DPSK
M-PAM
M-QAM
Ортогональный M-FSK с когерентным обнаружением
Неортогональный 2-FSK с когерентным обнаружением
Ортогональный M-FSK с некогерентным обнаружением
Неортогональный 2-FSK с некогерентным обнаружением
Предварительно закодированный MSK с когерентным обнаружением
Дифференцированно закодированный MSK с когерентным обнаружением
MSK с некогерентным обнаружением (оптимальный блок блоком)
CPFSK когерентное обнаружение (оптимальный блок блоком)

M-PSK. От уравнения 8.22 в [2]

$P_{s} = \frac{1}{π} \int_{0}^{(M - 1) π / M} \exp (- \frac{k E_{b}}{N_{0}} \frac{\sin^{2} [π / M]}{\sin^{2} θ}) d θ$

Следующее выражение очень близко, но не строго равно к точному BER (от [4] и уравнение 8.29 от [2]):

$P_{b} = \frac{1}{k} (\sum_{i = 1}^{M / 2} (w_{i}^{'}) P_{i})$

где $w_{i}^{'} = w_{i} + w_{M - i}$ , $w_{M / 2}^{'} = w_{M / 2}$ , $w_{i}$ вес Хэмминга битов, присвоенных символу i, и

$\begin{matrix} P_{i} = \frac{1}{2 π} \int_{0}^{π (1 - (2 i - 1) / M)} \exp (- \frac{k E_{b}}{N_{0}} \frac{\sin^{2} [(2 i - 1) π / M]}{\sin^{2} θ}) d θ \\ - \frac{1}{2 π} \int_{0}^{π (1 - (2 i + 1) / M)} \exp (- \frac{k E_{b}}{N_{0}} \frac{\sin^{2} [(2 i + 1) π / M]}{\sin^{2} θ}) d θ \end{matrix}$

Особый случай $M = 2$ , например, BPSK (уравнение 5.2-57 от [1]):

$P_{s} = P_{b} = Q (\sqrt{\frac{2 E_{b}}{N_{0}}})$

Особый случай $M = 4$ , например, QPSK (уравнения 5.2-59 и 5.2-62 от [1]):

$\begin{matrix} P_{s} = 2 Q (\sqrt{\frac{2 E_{b}}{N_{0}}}) [1 - \frac{}{12} Q (\sqrt{\frac{2 E_{b}}{N_{0}}})] \\ P_{b} = Q (\sqrt{\frac{2 E_{b}}{N_{0}}}) \end{matrix}$

DE-M-PSK. $M = 2$ , например, DE-BPSK (уравнение 8.36 от [2]):

$P_{s} = P_{b} = 2 Q (\sqrt{\frac{2 E_{b}}{N_{0}}}) - 2 Q^{2} (\sqrt{\frac{2 E_{b}}{N_{0}}})$

$M = 4$ , например, DE-QPSK (уравнение 8.38 от [2]):

$P_{s} = 4 Q (\sqrt{\frac{2 E_{b}}{N_{0}}}) - 8 Q^{2} (\sqrt{\frac{2 E_{b}}{N_{0}}}) + 8 Q^{3} (\sqrt{\frac{2 E_{b}}{N_{0}}}) - 4 Q^{4} (\sqrt{\frac{2 E_{b}}{N_{0}}})$

От уравнения 5 в [3]:

$P_{b} = 2 Q (\sqrt{\frac{2 E_{b}}{N_{0}}}) [1 - Q (\sqrt{\frac{2 E_{b}}{N_{0}}})]$

OQPSK. Тот же BER/SER как QPSK [2].

DE-OQPSK. Тот же BER/SER как DE-QPSK [3].

M-DPSK. От уравнения 8.84 в [2]:

$P_{s} = \frac{\sin (π / M)}{2 π} \int_{- π / 2}^{π / 2} \frac{\exp (- (k E_{b} / N_{0}) (1 - потому что (π / M) потому что θ))}{1 - потому что (π / M) потому что θ} d θ$

Следующее выражение очень близко, но не строго равно к точному BER [4]:

$P_{b} = \frac{1}{k} (\sum_{i = 1}^{M / 2} (w_{i}^{'}) A_{i})$

где $w_{i}^{'} = w_{i} + w_{M - i}$ , $w_{M / 2}^{'} = w_{M / 2}$ , $w_{i}$ вес Хэмминга битов, присвоенных символу i, и

$\begin{array}{l} A_{i} = F ((2 i + 1) \frac{π}{M}) - F ((2 i - 1) \frac{π}{M}) \\ F (ψ) = - \frac{\sin ψ}{4 π} \int_{- π / 2}^{π / 2} \frac{\exp (- k E_{b} / N_{0} (1 - потому что ψ потому что t))}{1 - потому что ψ потому что t} d t \end{array}$

Особый случай $M = 2$ (уравнение 8.85 от [2]):

$P_{b} = \frac{}{12} \exp (- \frac{E_{b}}{N_{0}})$

M-PAM. От уравнений 8.3 и 8.7 в [2] и уравнения 5.2-46 в [1]:

$P_{s} = 2 (\frac{M - 1}{M}) Q (\sqrt{\frac{6}{M^{2} - 1} \frac{k E_{b}}{N_{0}}})$

От [5]:

$\begin{matrix} P_{b} = \frac{2}{M {журнал}_{2} M} \times \\ \sum_{k = 1}^{{журнал}_{2} M} \sum_{i = 0}^{(1 - 2^{- k}) M - 1} {{(- 1)}^{⌊ \frac{i 2^{k - 1}}{M} ⌋} (2^{k - 1} - ⌊ \frac{i 2^{k - 1}}{M} + \frac{}{12} ⌋) Q ((2 i + 1) \sqrt{\frac{6 {журнал}_{2} M}{M^{2} - 1} \frac{E_{b}}{N_{0}}})} \end{matrix}$

M-QAM. Для квадратного M-QAM, $k = {журнал}_{2} M$ даже (уравнение 8.10 от [2] и уравнения 5.2-78 и 5.2-79 от [1]):

$P_{s} = 4 \frac{\sqrt{M} - 1}{\sqrt{M}} Q (\sqrt{\frac{3}{M - 1} \frac{k E_{b}}{N_{0}}}) - 4 {(\frac{\sqrt{M} - 1}{\sqrt{M}})}^{2} Q^{2} (\sqrt{\frac{3}{M - 1} \frac{k E_{b}}{N_{0}}})$

От [5]:

$\begin{matrix} P_{b} = \frac{2}{\sqrt{M} {журнал}_{2} \sqrt{M}} \\ \times \sum_{k = 1}^{{журнал}_{2} \sqrt{M}} \sum_{i = 0}^{(1 - 2^{- k}) \sqrt{M} - 1} {{(- 1)}^{⌊ \frac{i 2^{k - 1}}{\sqrt{M}} ⌋} (2^{k - 1} - ⌊ \frac{i 2^{k - 1}}{\sqrt{M}} + \frac{}{12} ⌋) Q ((2 i + 1) \sqrt{\frac{6 {журнал}_{2} M}{2 (M - 1)} \frac{E_{b}}{N_{0}}})} \end{matrix}$

Для прямоугольного (неквадратного) M-QAM, $k = {журнал}_{2} M$ нечетно, $M = I \times J$ , $I = 2^{\frac{k - 1}{2}}$ , и $J = 2^{\frac{k + 1}{2}}$ :

$\begin{matrix} P_{s} = \frac{4 I J - 2 I - 2 J}{M} \\ \times Q (\sqrt{\frac{6 {журнал}_{2} (I J)}{(I^{2} + J^{2} - 2)} \frac{E_{b}}{N_{0}}}) - \frac{4}{M} (1 + I J - I - J) Q^{2} (\sqrt{\frac{6 {журнал}_{2} (I J)}{(I^{2} + J^{2} - 2)} \frac{E_{b}}{N_{0}}}) \end{matrix}$

От [5]:

$P_{b} = \frac{1}{{журнал}_{2} (I J)} (\sum_{k = 1}^{{журнал}_{2} I} P_{I} (k) + \sum_{l = 1}^{{журнал}_{2} J} P_{J} (l))$

где

$P_{I} (k) = \frac{2}{I} \sum_{i = 0}^{(1 - 2^{- k}) I - 1} {{(- 1)}^{⌊ \frac{i 2^{k - 1}}{I} ⌋} (2^{k - 1} - ⌊ \frac{i 2^{k - 1}}{I} + \frac{}{12} ⌋) Q ((2 i + 1) \sqrt{\frac{6 {журнал}_{2} (I J)}{I^{2} + J^{2} - 2} \frac{E_{b}}{N_{0}}})}$

$P_{J} (k) = \frac{2}{J} \sum_{j = 0}^{(1 - 2^{- l}) J - 1} {{(- 1)}^{⌊ \frac{j 2^{l - 1}}{J} ⌋} (2^{l - 1} - ⌊ \frac{j 2^{l - 1}}{J} + \frac{}{12} ⌋) Q ((2 j + 1) \sqrt{\frac{6 {журнал}_{2} (I J)}{I^{2} + J^{2} - 2} \frac{E_{b}}{N_{0}}})}$

Ортогональный M-FSK с Когерентным Обнаружением. От уравнения 8.40 в [2] и уравнения 5.2-21 в [1]:

$\begin{array}{l} P_{s} = 1 - \int_{- \infty}^{\infty} {[Q (- q - \sqrt{\frac{2 k E_{b}}{N_{0}}})]}^{M - 1} \frac{1}{\sqrt{2 π}} \exp (- \frac{q^{2}}{2}) d q \\ P_{b} = \frac{2^{k - 1}}{2^{k} - 1} P_{s} \end{array}$

Неортогональный 2-FSK с когерентным обнаружением. Для $M = 2$ (от уравнения 5.2-21 в [1] и уравнения 8.44 в [2]):

$P_{s} = P_{b} = Q (\sqrt{\frac{E_{b} (1 - Ре [ρ])}{N_{0}}})$

$ρ$ комплексный коэффициент корреляции:

$ρ = \frac{1}{2 E_{b}} \int_{0}^{T_{b}} {\tilde{s}}_{1} (t) {\tilde{s}}_{2}^{*} (t) d t$

где ${\tilde{s}}_{1} (t)$ и ${\tilde{s}}_{2} (t)$ комплексные сигналы lowpass, и

$E_{b} = \frac{}{12} \int_{0}^{T_{b}} {| {\tilde{s}}_{1} (t) |}^{2} d t = \frac{}{12} \int_{0}^{T_{b}} {| {\tilde{s}}_{2} (t) |}^{2} d t$

Например:

${\tilde{s}}_{1} (t) = \sqrt{\frac{2 E_{b}}{T_{b}}} e^{j 2 π f_{1} t}, {\tilde{s}}_{2} (t) = \sqrt{\frac{2 E_{b}}{T_{b}}} e^{j 2 π f_{2} t}$

$\begin{matrix} ρ = \frac{1}{2 E_{b}} \int_{0}^{T_{b}} \sqrt{\frac{2 E_{b}}{T_{b}}} e^{j 2 π f_{1} t} \sqrt{\frac{2 E_{b}}{T_{b}}} e^{- j 2 π f_{2} t} d t = \frac{1}{T_{b}} \int_{0}^{T_{b}} e^{j 2 π (f_{1} - f_{2}) t} d t \\ = \frac{\sin (π Δ f T_{b})}{π Δ f T_{b}} e^{j π Δ f t} \end{matrix}$

где $Δ f = f_{1} - f_{2}$ .

$\begin{array}{l} Ре [ρ] = Ре [\frac{\sin (π Δ f T_{b})}{π Δ f T_{b}} e^{j π Δ f t}] = \frac{\sin (π Δ f T_{b})}{π Δ f T_{b}} потому что (π Δ f T_{b}) = \frac{\sin (2 π Δ f T_{b})}{2 π Δ f T_{b}} \\ \Rightarrow P_{b} = Q (\sqrt{\frac{E_{b} (1 - \sin (2 π Δ f T_{b}) / (2 π Δ f T_{b}))}{N_{0}}}) \end{array}$

(от уравнения 8.44 в [2], где $h = Δ f T_{b}$ )

Ортогональный M-FSK с Некогерентным Обнаружением. От уравнения 5.4-46 в [1] и уравнения 8.66 в [2]:

$\begin{array}{l} P_{s} = \sum_{m = 1}^{M - 1} {(- 1)}^{m + 1} (\begin{matrix} M - 1 \\ m \end{matrix}) \frac{1}{m + 1} \exp [- \frac{m}{m + 1} \frac{k E_{b}}{N_{0}}] \\ P_{b} = \frac{}{12} \frac{M}{M - 1} P_{s} \end{array}$

Неортогональный 2-FSK с некогерентным обнаружением. Для $M = 2$ (от уравнения 5.4-53 в [1] и уравнения 8.69 в [2]):

$P_{s} = P_{b} = Q (\sqrt{a}, \sqrt{b}) - \frac{}{12} \exp (- \frac{a + b}{2}) I_{0} (\sqrt{a b})$

где

$a = \frac{E_{b}}{2 N_{0}} (1 - \sqrt{1 - {| ρ |}^{2}}), b = \frac{E_{b}}{2 N_{0}} (1 + \sqrt{1 - {| ρ |}^{2}})$

Предварительно закодированный MSK с когерентным обнаружением. Тот же BER/SER как BPSK.

Дифференцированно закодированный MSK с когерентным обнаружением. Тот же BER/SER как DE-BPSK.

MSK с Некогерентным Обнаружением (Оптимальный Блок Блоком). Верхняя граница (от уравнений 10.166 и 10.164 в [6]):

$\begin{matrix} P_{s} = P_{b} \\ \leq \frac{}{12} [1 - Q (\sqrt{b_{1}}, \sqrt{a_{1}}) + Q (\sqrt{a_{1}}, \sqrt{b_{1}})] + \frac{}{14} [1 - Q (\sqrt{b_{4}}, \sqrt{a_{4}}) + Q (\sqrt{a_{4}}, \sqrt{b_{4}})] + \frac{}{12} e^{- \frac{E_{b}}{N_{0}}} \end{matrix}$

где

$\begin{matrix} a_{1} = \frac{E_{b}}{N_{0}} (1 - \sqrt{\frac{3 - 4 / π^{2}}{4}}), & b_{1} = \frac{E_{b}}{N_{0}} (1 + \sqrt{\frac{3 - 4 / π^{2}}{4}}) \\ a_{4} = \frac{E_{b}}{N_{0}} (1 - \sqrt{1 - 4 / π^{2}}), & b_{4} = \frac{E_{b}}{N_{0}} (1 + \sqrt{1 - 4 / π^{2}}) \end{matrix}$

CPFSK Когерентное Обнаружение (Оптимальный Блок Блоком). Нижняя граница (от уравнения 5.3-17 в [1]):

$P_{s} > K_{δ_{\min}} Q (\sqrt{\frac{E_{b}}{N_{0}} δ_{\min}^{2}})$

Верхняя граница:

$δ_{\min}^{2} > \min_{1 \leq i \leq M - 1} {2 i (1 - sinc (2 i h))}$

где h является индексом модуляции, и $K_{δ_{\min}}$ количество путей, имеющих минимальное расстояние.

$P_{b} ≅ \frac{P_{s}}{k}$

Аналитические Выражения, Используемые в berfading

Обозначение
M-PSK с MRC
DE-M-PSK с MRC
M-PAM с MRC
M-QAM с MRC
M-DPSK с постобнаружением EGC
Ортогональный 2-FSK, когерентное обнаружение с MRC
Неортогональный 2-FSK, когерентное обнаружение с MRC
Ортогональный M-FSK, некогерентное обнаружение с EGC
Неортогональный 2-FSK, некогерентное обнаружение без разнообразия

Обозначение. Следующее обозначение используется для выражений, найденных в berfading.

Значение	Обозначение
Степень исчезающего амплитудного r	$Ω = E [r^{2}]$ , где $E [\cdot]$ обозначает статистическое ожидание
Количество ответвлений разнообразия	$L$
ОСШ на символ на ответвление	${\bar{γ}}_{l} = (Ω_{l} \frac{E_{s}}{N_{0}}) / L = (Ω_{l} \frac{k E_{b}}{N_{0}}) / L$ Для тождественно распределенных ответвлений разнообразия: $\bar{γ} = (Ω \frac{k E_{b}}{N_{0}}) / L$
Производящие функции момента для каждого ответвления разнообразия	Релеевское замирание: $M_{γ_{l}} (s) = \frac{1}{1 - s {\bar{γ}}_{l}}$ Исчезновение Rician: $M_{γ_{l}} (s) = \frac{1 + K}{1 + K - s {\bar{γ}}_{l}} e^{[\frac{K s {\bar{γ}}_{l}}{(1 + K) - s {\bar{γ}}_{l}}]}$ где K является отношением энергии в зеркальном компоненте к энергии в рассеянном компоненте (линейная шкала). Для тождественно распределенных ответвлений разнообразия: $M_{γ_{l}} (s) = M_{γ} (s)$ для всего l.

Следующие акронимы используются:

Акроним	Определение
MRC	объединение максимального отношения
EGC	объединение равного усиления

M-PSK с MRC. От уравнения 9.15 в [2]:

$P_{s} = \frac{1}{π} \int_{0}^{(M - 1) π / M} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{\sin^{2} (π / M)}{\sin^{2} θ}) d θ$

От [4] и [2]:

$P_{b} = \frac{1}{k} (\sum_{i = 1}^{M / 2} (w_{i}^{'}) {\bar{P}}_{i})$

где $w_{i}^{'} = w_{i} + w_{M - i}$ , $w_{M / 2}^{'} = w_{M / 2}$ , $w_{i}$ вес Хэмминга битов, присвоенных символу i, и

$\begin{array}{l} {\bar{P}}_{i} = \frac{1}{2 π} \int_{0}^{π (1 - (2 i - 1) / M)} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{1}{\sin^{2} θ} \sin^{2} \frac{(2 i - 1) π}{M}) d θ \\ - \frac{1}{2 π} \int_{0}^{π (1 - (2 i + 1) / M)} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{1}{\sin^{2} θ} \sin^{2} \frac{(2 i + 1) π}{M}) d θ \end{array}$

Для особого случая Релеевского замирания с $M = 2$ (от уравнений C-18, C-21 и Таблица c-1 в [6]):

$P_{b} = \frac{}{12} [1 - μ \sum_{i = 0}^{L - 1} (\begin{matrix} 2 i \\ i \end{matrix}) {(\frac{1 - μ^{2}}{4})}^{i}]$

где

$μ = \sqrt{\frac{\bar{γ}}{\bar{γ} + 1}}$

Если $L = 1$ :

$P_{b} = \frac{}{12} [1 - \sqrt{\frac{\bar{γ}}{\bar{γ} + 1}}]$

DE-M-PSK с MRC. Для $M = 2$ (от уравнений 8.37 и 9.8-9.11 в [2]):

$P_{s} = P_{b} = \frac{2}{π} \int_{0}^{π / 2} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{1}{\sin^{2} θ}) d θ - \frac{2}{π} \int_{0}^{π / 4} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{1}{\sin^{2} θ}) d θ$

M-PAM с MRC. От уравнения 9.19 в [2]:

$P_{s} = \frac{2 (M - 1)}{M π} \int_{0}^{π / 2} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{3 / (M^{2} - 1)}{\sin^{2} θ}) d θ$

От [5] и [2]:

$\begin{matrix} P_{b} = \frac{2}{π M {журнал}_{2} M} \\ \times \sum_{k = 1}^{{журнал}_{2} M} \sum_{i = 0}^{(1 - 2^{- k}) M - 1} {{(- 1)}^{⌊ \frac{i 2^{k - 1}}{M} ⌋} (2^{k - 1} - ⌊ \frac{i 2^{k - 1}}{M} + \frac{}{12} ⌋) \int_{0}^{π / 2} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{{(2 i + 1)}^{} 23 / (M^{2} - 1)}{\sin^{2} θ}) d θ} \end{matrix}$

M-QAM с MRC. Для квадратного M-QAM, $k = {журнал}_{2} M$ даже (уравнение 9.21 в [2]):

$\begin{matrix} P_{s} = \frac{4}{π} (1 - \frac{1}{\sqrt{M}}) \int_{0}^{π / 2} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{3 / (2 (M - 1))}{\sin^{2} θ}) d θ \\ - \frac{4}{π} {(1 - \frac{1}{\sqrt{M}})}^{2} \int_{0}^{π / 4} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{3 / (2 (M - 1))}{\sin^{2} θ}) d θ \end{matrix}$

От [5] и [2]:

$\begin{matrix} P_{b} = \frac{2}{π \sqrt{M} {журнал}_{2} \sqrt{M}} \\ \times \sum_{k = 1}^{{журнал}_{2} \sqrt{M}} \sum_{i = 0}^{(1 - 2^{- k}) \sqrt{M} - 1} {{(- 1)}^{⌊ \frac{i 2^{k - 1}}{\sqrt{M}} ⌋} (2^{k - 1} - ⌊ \frac{i 2^{k - 1}}{\sqrt{M}} + \frac{}{12} ⌋) \int_{0}^{π / 2} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{{(2 i + 1)}^{} 23 / (2 (M - 1))}{\sin^{2} θ}) d θ} \end{matrix}$

Для прямоугольного (неквадратного) M-QAM, $k = {журнал}_{2} M$ нечетно, $M = I \times J$ , $I = 2^{\frac{k - 1}{2}}$ , $J = 2^{\frac{k + 1}{2}}$ , ${\bar{γ}}_{l} = Ω_{l} {журнал}_{2} (I J) \frac{E_{b}}{N_{0}}$ , и

$\begin{matrix} P_{s} = \frac{4 I J - 2 I - 2 J}{M π} \int_{0}^{π / 2} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{3 / (I^{2} + J^{2} - 2)}{\sin^{2} θ}) d θ \\ - \frac{4}{M π} (1 + I J - I - J) \int_{0}^{π / 4} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{3 / (I^{2} + J^{2} - 2)}{\sin^{2} θ}) d θ \end{matrix}$

От [5] и [2]:

$\begin{matrix} P_{b} = \frac{1}{{журнал}_{2} (I J)} (\sum_{k = 1}^{{журнал}_{2} I} P_{I} (k) + \sum_{l = 1}^{{журнал}_{2} J} P_{J} (l)) \\ P_{I} (k) = \frac{2}{I π} \sum_{i = 0}^{(1 - 2^{- k}) I - 1} {{(- 1)}^{⌊ \frac{i 2^{k - 1}}{I} ⌋} (2^{k - 1} - ⌊ \frac{i 2^{k - 1}}{I} + \frac{}{12} ⌋) \int_{0}^{π / 2} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{{(2 i + 1)}^{} 23 / (I^{2} + J^{2} - 2)}{\sin^{2} θ}) d θ} \\ P_{J} (k) = \frac{2}{J π} \sum_{j = 0}^{(1 - 2^{- l}) J - 1} {{(- 1)}^{⌊ \frac{j 2^{l - 1}}{J} ⌋} (2^{l - 1} - ⌊ \frac{j 2^{l - 1}}{J} + \frac{}{12} ⌋) \int_{0}^{π / 2} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{{(2 j + 1)}^{} 23 / (I^{2} + J^{2} - 2)}{\sin^{2} θ}) d θ} \end{matrix}$

M-DPSK с Постобнаружением EGC. От уравнения 8.165 в [2]:

$P_{s} = \frac{\sin (π / M)}{2 π} \int_{- π / 2}^{π / 2} \frac{1}{[1 - потому что (π / M) потому что θ]} \prod_{l = 1}^{L} M_{γ_{l}} (- [1 - потому что (π / M) потому что θ]) d θ$

От [4] и [2]:

$P_{b} = \frac{1}{k} (\sum_{i = 1}^{M / 2} (w_{i}^{'}) {\bar{A}}_{i})$

где $w_{i}^{'} = w_{i} + w_{M - i}$ , $w_{M / 2}^{'} = w_{M / 2}$ , $w_{i}$ вес Хэмминга битов, присвоенных символу i, и

$\begin{array}{l} {\bar{A}}_{i} = \bar{F} ((2 i + 1) \frac{π}{M}) - \bar{F} ((2 i - 1) \frac{π}{M}) \\ \bar{F} (ψ) = - \frac{\sin ψ}{4 π} \int_{- π / 2}^{π / 2} \frac{1}{(1 - потому что ψ потому что t)} \prod_{l = 1}^{L} M_{γ_{l}} (- (1 - потому что ψ потому что t)) d t \end{array}$

Для особого случая Релеевского замирания с $M = 2$ , и $L = 1$ (уравнение 8.173 от [2]):

$P_{b} = \frac{1}{2 (1 + \bar{γ})}$

Ортогональный 2-FSK, Когерентное Обнаружение с MRC. От уравнения 9.11 в [2]:

$P_{s} = P_{b} = \frac{1}{π} \int_{0}^{π / 2} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{1 / 2}{\sin^{2} θ}) d θ$

Для особого случая Релеевского замирания (уравнения 14.4-15 и 14.4-21 в [1]):

$P_{s} = P_{b} = \frac{1}{2^{L}} {(1 - \sqrt{\frac{\bar{γ}}{2 + \bar{γ}}})}^{L} \sum_{k = 0}^{L - 1} (\begin{matrix} L - 1 + k \\ k \end{matrix}) \frac{1}{2^{k}} {(1 + \sqrt{\frac{\bar{γ}}{2 + \bar{γ}}})}^{k}$

Неортогональный 2-FSK, когерентное обнаружение с MRC. Уравнения 9.11 и 8.44 в [2]:

$P_{s} = P_{b} = \frac{1}{π} \int_{0}^{π / 2} \prod_{l = 1}^{L} M_{γ_{l}} (- \frac{(1 - Ре [ρ]) / 2}{\sin^{2} θ}) d θ$

Для особого случая Релеевского замирания с $L = 1$ (уравнение 20 в [8] и уравнение 8.130 в [2]):

$P_{s} = P_{b} = \frac{}{12} [1 - \sqrt{\frac{\bar{γ} (1 - Ре [ρ])}{2 + \bar{γ} (1 - Ре [ρ])}}]$

Ортогональный M-FSK, Некогерентное Обнаружение с EGC. Релеевское замирание (уравнение 14.4-47 в [1]):

$\begin{array}{l} P_{s} = 1 - \int_{0}^{\infty} \frac{1}{{(1 + \bar{γ})}^{L} (L - 1)!} U^{L - 1} e^{- \frac{U}{1 + \bar{γ}}} {(1 - e^{- U} \sum_{k = 0}^{L - 1} \frac{U^{k}}{k!})}^{M - 1} d U \\ P_{b} = \frac{}{12} \frac{M}{M - 1} P_{s} \end{array}$

Исчезновение Rician (уравнение 41 в [8]):

$\begin{array}{l} P_{s} = \sum_{r = 1}^{M - 1} \frac{{(- 1)}^{r + 1} e^{- L K {\bar{γ}}_{r} / (1 + {\bar{γ}}_{r})}}{{(r (1 + {\bar{γ}}_{r}) + 1)}^{L}} (\begin{matrix} M - 1 \\ r \end{matrix}) \sum_{n = 0}^{r (L - 1)} β_{n r} \frac{Γ (L + n)}{Γ (L)} {[\frac{1 + {\bar{γ}}_{r}}{r + 1 + r {\bar{γ}}_{r}}]}^{n} {}_{1}F_{1} (L + n, L; \frac{L K {\bar{γ}}_{r} / (1 + {\bar{γ}}_{r})}{r (1 + {\bar{γ}}_{r}) + 1}) \\ P_{b} = \frac{}{12} \frac{M}{M - 1} P_{s} \end{array}$

где

$\begin{matrix} {\bar{γ}}_{r} = \frac{1}{1 + K} \bar{γ} \\ β_{n r} = \sum_{i = n - (L - 1)}^{n} \frac{β_{i (r - 1)}}{(n - i)!} I_{[0, (r - 1) (L - 1)]} (i) \\ β_{00} = β_{0 r} = 1 \\ β_{n 1} = 1 / n! \\ β_{1 r} = r \end{matrix}$

и $I_{[a, b]} (i) = 1$ если $a \leq i \leq b$ и 0 в противном случае.

Неортогональный 2-FSK, Некогерентное Обнаружение без Разнообразия. От уравнения 8.163 в [2]:

$P_{s} = P_{b} = \frac{1}{4 π} \int_{- π}^{π} \frac{1 - ς^{2}}{1 + 2 ς \sin θ + ς^{2}} M_{γ} (- \frac{}{14} (1 + \sqrt{1 - ρ^{2}}) (1 + 2 ς \sin θ + ς^{2})) d θ$

где

$ς = \sqrt{\frac{1 - \sqrt{1 - ρ^{2}}}{1 + \sqrt{1 - ρ^{2}}}}$

Аналитические Выражения, Используемые в bercoding и BERTool

Общее обозначение для этого раздела
Блочное кодирование
Сверточное кодирование

Общее обозначение для этого раздела

Описание	Обозначение
Отношение спектральной плотности степени бита к шуму энергии на информацию	$γ_{b} = \frac{E_{b}}{N_{0}}$
Передайте длину	$K$
Разрядность кода	$N$
Уровень кода	$R_{c} = \frac{K}{N}$

Блочное кодирование. Определенное обозначение для выражений блочного кодирования: $d_{\min}$ минимальное расстояние кода.

Мягкое решение

BPSK, QPSK, OQPSK, PAM-2, QAM-4 и предварительно закодированный MSK (уравнение 8.1-52 в [1]):

$P_{b} \leq \frac{}{12} (2^{K} - 1) Q (\sqrt{2 γ_{b} R_{c} d_{\min}})$

DE-BPSK, DE-QPSK, DE-OQPSK и DE-MSK:

$P_{b} \leq \frac{}{12} (2^{K} - 1) [2 Q (\sqrt{2 γ_{b} R_{c} d_{\min}}) [1 - Q (\sqrt{2 γ_{b} R_{c} d_{\min}})]]$

BFSK, когерентное обнаружение (уравнения 8.1-50 и 8.1-58 в [1]):

$P_{b} \leq \frac{}{12} (2^{K} - 1) Q (\sqrt{γ_{b} R_{c} d_{\min}})$

BFSK, некогерентное квадратичное обнаружение (уравнения 8.1-65 и 8.1-64 в [1]):

$P_{b} \leq \frac{}{12} \frac{2^{K} - 1}{2^{2 d_{\min} - 1}} \exp (- \frac{}{12} γ_{b} R_{c} d_{\min}) \sum_{i = 0}^{d_{\min} - 1} {(\frac{}{12} γ_{b} R_{c} d_{\min})}^{i} \frac{1}{i!} \sum_{r = 0}^{d_{\min} - 1 - i} (\begin{matrix} 2 d_{\min} - 1 \\ r \end{matrix})$

DPSK:

$P_{b} \leq \frac{}{12} \frac{2^{K} - 1}{2^{2 d_{\min} - 1}} \exp (- γ_{b} R_{c} d_{\min}) \sum_{i = 0}^{d_{\min} - 1} {(γ_{b} R_{c} d_{\min})}^{i} \frac{1}{i!} \sum_{r = 0}^{d_{\min} - 1 - i} (\begin{matrix} 2 d_{\min} - 1 \\ r \end{matrix})$

Трудное решение

Общий линейный блочный код (уравнения 4.3, 4.4 в [9], и 12.136 в [6]):

$\begin{array}{l} P_{b} \leq \frac{1}{N} \sum_{m = t + 1}^{N} (m + t) (\begin{matrix} N \\ m \end{matrix}) p^{m} {(1 - p)}^{N - m} \\ t = ⌊ \frac{}{12} (d_{\min} - 1) ⌋ \end{array}$

Код Хемминга (уравнения 4.11, 4.12 в [9], и 6.72, 6.73 в [7]):

$P_{b} \approx \frac{1}{N} \sum_{m = 2}^{N} m (\begin{matrix} N \\ m \end{matrix}) p^{m} {(1 - p)}^{N - m} = p - p {(1 - p)}^{N - 1}$

(24, 12), расширил код Golay (уравнение 4.17 в [9], и 12.139 в [6]):

$P_{b} \leq \frac{1}{24} \sum_{m = 4}^{24} β_{m} (\begin{matrix} 24 \\ m \end{matrix}) p^{m} {(1 - p)}^{24 - m}$

где $β_{m}$ среднее количество ошибок символа канала, которые остаются в исправленном N - кортеж, когда канал вызвал ошибки символа m (таблица 4.2 в [9]).

Код тростника-Solomon с $N = Q - 1 = 2^{q} - 1$ :

$P_{b} \approx \frac{2^{q - 1}}{2^{q} - 1} \frac{1}{N} \sum_{m = t + 1}^{N} m (\begin{matrix} N \\ m \end{matrix}) {(P_{s})}^{m} {(1 - P_{s})}^{N - m}$

для FSK (уравнения 4.25, 4.27 в [9], 8.1-115, 8.1-116 в [1], 8.7, 8.8 в [7], и 12.142, 12.143 в [6]), и

$P_{b} \approx \frac{1}{q} \frac{1}{N} \sum_{m = t + 1}^{N} m (\begin{matrix} N \\ m \end{matrix}) {(P_{s})}^{m} {(1 - P_{s})}^{N - m}$

в противном случае.

Если ${журнал}_{2} Q / {журнал}_{2} M = q / k = h$ где h является целым числом (уравнение 1 в [10]):

$P_{s} = 1 - {(1 - s)}^{h}$

где s является коэффициентом ошибок символа (SER) в незакодированном канале AWGN.

Например, для BPSK, $M = 2$ и $P_{s} = 1 - {(1 - s)}^{q}$

В противном случае, $P_{s}$ дан таблицей 1 и уравнением 2 в [10].

Сверточное Кодирование. Определенное обозначение для сверточных выражений кодирования: $d_{f r e e}$ свободное расстояние кода, и $a_{d}$ количество путей расстояния d от все-нулевого пути, которые объединяют со все-нулевым путем впервые.

Мягкое решение

От уравнений 8.2-26, 8.2-24, и 8.2-25 в [1], и уравнений 13.28 и 13.27 в [6]:

$P_{b} < \sum_{d = d_{f r e e}}^{\infty} a_{d} f (d) P_{2} (d)$

с передаточной функцией

$\begin{array}{l} T (D, N) = \sum_{d = d_{f r e e}}^{\infty} a_{d} D^{d} N^{f (d)} \\ {\frac{d T (D, N)}{d N} |}_{N = 1} = \sum_{d = d_{f r e e}}^{\infty} a_{d} f (d) D^{d} \end{array}$

где $f (d)$ экспонента N как функция d.

Результаты для BPSK, QPSK, OQPSK, PAM-2, QAM-4, предварительно закодировали MSK, DE-BPSK, DE-QPSK, DE-OQPSK, DE-MSK, DPSK, и BFSK получен как:

$P_{2} (d) = {P_{b} |}_{\frac{E_{b}}{N_{0}} = γ_{b} R_{c} d}$

где $P_{b}$ BER в соответствующем незакодированном канале AWGN. Например, для BPSK (уравнение 8.2-20 в [1]):

$P_{2} (d) = Q (\sqrt{2 γ_{b} R_{c} d})$

Трудное решение

От уравнений 8.2-33, 8.2-28, и 8.2-29 в [1], и уравнений 13.28, 13.24, и 13.25 в [6]:

$P_{b} < \sum_{d = d_{f r e e}}^{\infty} a_{d} f (d) P_{2} (d)$

где

$P_{2} (d) = \sum_{k = (d + 1) / 2}^{d} (\begin{matrix} d \\ k \end{matrix}) p^{k} {(1 - p)}^{d - k}$

когда d нечетен, и

$P_{2} (d) = \sum_{k = d / 2 + 1}^{d} (\begin{matrix} d \\ k \end{matrix}) p^{k} {(1 - p)}^{d - k} + \frac{}{12} (\begin{matrix} d \\ d / 2 \end{matrix}) p^{d / 2} {(1 - p)}^{d / 2}$

когда d даже (p является частотой ошибок по битам (BER) в незакодированном канале AWGN).

Результаты производительности через Симуляцию

Разделите обзор
Используя моделируемые данные, чтобы вычислить коэффициенты ошибок бита и символа
Пример: вычисление коэффициентов ошибок
Сравнение коэффициента ошибок символа и частоты ошибок по битам

Разделите обзор

Один способ вычислить частоту ошибок по битам или коэффициент ошибок символа для системы связи состоит в том, чтобы моделировать передачу сообщений данных и сравнить все сообщения до и после передачи. Симуляция компонентов системы связи с помощью Communications Toolbox™ покрыта другими частями этого руководства. В этом разделе описывается сравнить сообщения данных, которые вводят и оставляют симуляцию.

Другой пример вычислительных результатов производительности через симуляцию находится в Curve Fitting для Графиков Коэффициента ошибок в обсуждении аппроксимирования кривыми.

Используя моделируемые данные, чтобы вычислить коэффициенты ошибок бита и символа

Функция biterr сравнивает два набора данных и вычисляет количество битовых ошибок и частоты ошибок по битам. Функция symerr сравнивает два набора данных и вычисляет количество ошибок символа и коэффициента ошибок символа. Ошибка является несоответствием между соответствующими точками в двух наборах данных.

Из двух наборов данных обычно каждый представляет сообщения, вводящие передатчик, и другой представляет восстановленные сообщения, оставляя получатель. Вы можете также сравнить ввод данных и отъезд других частей вашей системы связи, например, данные, вводящие энкодер и данные, оставив декодер.

Если ваша система связи использует несколько битов, чтобы представлять один символ, подсчет битовых ошибок отличается от подсчета ошибок символа. Или в бите - или в считающем символ случае, коэффициент ошибок является количеством ошибок, разделенных на общее количество (битов или символов) переданный.

Примечание

Чтобы гарантировать точный коэффициент ошибок, необходимо обычно моделировать достаточно данных, чтобы произвести по крайней мере 100 ошибок.

Если коэффициент ошибок является очень небольшим (например, ^10-6 или меньшим), полуаналитический метод может вычислить результат более быстро, чем подход только для симуляции. Смотрите Результаты Производительности через Полуаналитический Метод для получения дополнительной информации о том, как использовать этот метод.

Пример: вычисление коэффициентов ошибок

Скрипт ниже использует функцию symerr, чтобы вычислить коэффициенты ошибок символа для шумного линейного блочного кода. После искусственного добавления шума к закодированному сообщению это сравнивает получившийся шумный код с оригинальным кодом. Затем это декодирует и сравнивает декодируемое сообщение с исходным.

m = 3; n = 2^m-1; k = n-m; % Prepare to use Hamming code.
msg = randi([0 1],k*200,1); % 200 messages of k bits each
code = encode(msg,n,k,'hamming');
codenoisy = rem(code+(rand(n*200,1)>.95),2); % Add noise.
% Decode and correct some errors.
newmsg = decode(codenoisy,n,k,'hamming');
% Compute and display symbol error rates.
noisyVec = step(comm.ErrorRate,code,codenoisy);
decodedVec = step(comm.ErrorRate,msg,newmsg);
disp(['Error rate in the received code: ',num2str(noisyVec(1))])
disp(['Error rate after decoding: ',num2str(decodedVec(1))])

Вывод ниже. Уменьшения коэффициента ошибок после декодирования, потому что декодер Хэмминга исправляет некоторые ошибки. Ваши результаты могут отличаться, потому что этот пример использует случайные числа.

Error rate in the received code: 0.054286
Error rate after decoding: 0.03

Сравнение коэффициента ошибок символа и частоты ошибок по битам

В примере выше, ошибки символа и битовые ошибки являются тем же самым, потому что каждый символ немного. Команды ниже иллюстрируют различие между ошибками символа и битовыми ошибками в других ситуациях.

a = [1 2 3]'; b = [1 4 4]';
format rat % Display fractions instead of decimals.
% Create ErrorRate Calculator System object
serVec = step(comm.ErrorRate,a,b);
srate = serVec(1)
snum = serVec(2)
% Convert integers to bits
hIntToBit = comm.IntegerToBit(3);
a_bit = step(hIntToBit, a);
b_bit = step(hIntToBit, b);
% Calculate BER
berVec = step(comm.ErrorRate,a_bit,b_bit);
brate = berVec(1)
bnum = berVec(2)

Вывод ниже.

snum =

      2      


srate =

     2/3     


bnum =

      5      


brate =

     5/9

bnum равняется 5, потому что вторые записи отличаются по двум битам, и третьи записи отличаются по трем битам. brate является 5/9, потому что общее количество битов равняется 9. Общее количество битов является, по определению, количеством записей в a или времена b максимальном количестве битов среди всех записей a и b.

Результаты производительности через Полуаналитический Метод

Метод, описанный в Результатах Производительности через Моделирование хорошо для большого множества систем связи, но, может быть предельно длительным, если коэффициент ошибок системы является очень небольшим (например, ^10-6 или меньшим). В этом разделе описывается использовать полуаналитический метод в качестве альтернативного способа вычислить коэффициенты ошибок. Для определенных типов систем полуаналитический метод может привести к результатам намного более быстро, чем неаналитический метод, который использует только моделируемые данные.

Полуаналитический метод использует комбинацию симуляции и анализа, чтобы определить коэффициент ошибок системы связи. Функция semianalytic в Communications Toolbox помогает вам реализовать полуаналитический метод путем выполнения части анализа.

Когда использовать полуаналитический метод

Полуаналитический метод работает хорошо на определенные типы систем связи, но не на других. Полуаналитический метод применим, если система имеет все эти характеристики:

Любые эффекты многопутевого исчезновения, квантования и нелинейности усилителя должны предшествовать эффектам шума в фактическом смоделированном канале.
Получатель отлично синхронизируется с поставщиком услуг, и синхронизирующий дрожание незначительно. Поскольку шум фазы и синхронизирующий дрожание является медленными процессами, они уменьшают применимость полуаналитического метода к системе связи.
Бесшумная симуляция не имеет никаких ошибок в полученном сигнальном созвездии. Искажения из источников кроме шума должны быть достаточно умеренными, чтобы сохранить каждую точку сигнала в ее правильной области решения. Если дело обстоит не так, расчетный BER является слишком низким. Например, если смоделированная система имеет вращение фазы, которое помещает полученные очки сигнала за пределами их соответствующих областей решения, полуаналитический метод не подходит, чтобы предсказать производительность системы.

Кроме того, функция semianalytic принимает, что шум в фактическом смоделированном канале является Гауссовым. Для получения дополнительной информации о том, как адаптировать полуаналитический метод к негауссову шуму, смотрите обсуждение обобщенных экспоненциальных распределений в [11].

Процедура для полуаналитического метода

Процедура ниже описывает, как вы обычно реализовывали бы полуаналитический метод с помощью функции semianalytic:

Сгенерируйте сигнал сообщения, содержащий, по крайней мере, символы ^ML, где M является размером алфавита модуляции, и L является продолжительностью импульсного ответа канала в символах. Общий подход должен запустить с увеличенного бинарного псевдошума (PN) последовательность общей длины _(log2M)ML. Увеличенная последовательность PN является последовательностью PN с дополнительным добавленным нулем, который делает распределение единиц и нулей равным.
Модулируйте поставщика услуг с сигналом сообщения использование основополосной модуляции. Поддерживаемые типы модуляции перечислены на странице с описанием для semianalytic. Сформируйте результирующий сигнал с формированием меандра, с помощью фактора сверхдискретизации, что вы будете дальнейшее использование, чтобы отфильтровать модулируемый сигнал. Сохраните результат этого шага как txsig для дальнейшего использования.
Отфильтруйте модулируемый сигнал с фильтром передачи. Этот фильтр часто является повышенным фильтром косинуса квадратного корня, но можно также использовать Баттерворта, функцию Бесселя, Чебышевский тип 1 или 2, эллиптического, или более общего КИХ или БИХ-фильтр. Если вы используете повышенный фильтр косинуса квадратного корня, используйте его на несверхдискретизированном модулируемом сигнале и укажите, что сверхдискретизация включает функцию фильтрации. Если вы используете другой тип фильтра, можно применить его к rectangularly сигналу импульсной формы.
Запустите пропущенный сигнал через бесшумный канал. Этот канал может включать многопутевые исчезающие эффекты, сдвиги фазы, нелинейность усилителя, квантование и дополнительную фильтрацию, но это не должно включать шум. Сохраните результат этого шага как rxsig для дальнейшего использования.
Вызовите функцию semianalytic использование txsig и данных rxsig из более ранних шагов. Задайте получить фильтр как пару входных параметров, если вы не хотите использовать фильтр функции по умолчанию. Функция фильтрует rxsig и затем определяет вероятность появления ошибки каждого полученного очка сигнала путем аналитичного применения Гауссова шумового распределения к каждой точке. Функциональные средние значения вероятности появления ошибки по целому полученному сигналу определить полную вероятность появления ошибки. Если вероятность появления ошибки, вычисленная таким образом, является вероятностью появления ошибки символа, функция преобразовывает ее в небольшой коэффициент ошибок, обычно путем принятия Грэя, кодирующего. Функция возвращает частоту ошибок по битам (или, в случае модуляции DQPSK, верхней границы на частоте ошибок по битам).

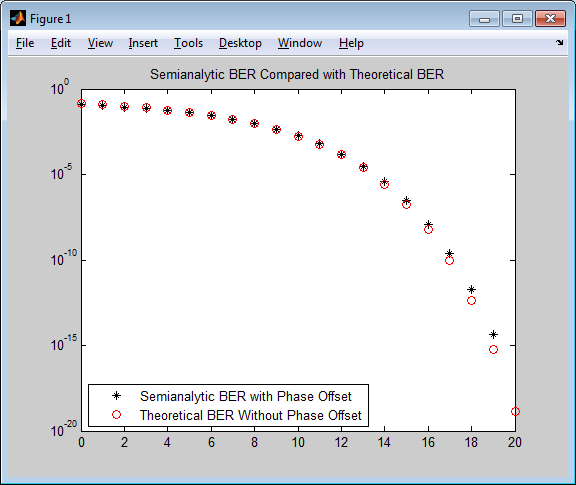
Пример: Используя полуаналитический метод

Пример ниже иллюстрирует процедуру, описанную выше, с помощью 16-QAM модуляции. Это также сравнивает коэффициенты ошибок, полученные из полуаналитического метода с теоретическими коэффициентами ошибок, полученными из опубликованных формул и вычисленного использования функции berawgn. Получившийся график показывает, что полученное использование коэффициентов ошибок этих двух методов почти идентично. Несоответствия между теоретическими и вычисленными коэффициентами ошибок происходят в основном из-за смещения фазы в модели канала этого примера.

% Step 1. Generate message signal of length >= M^L.
M = 16; % Alphabet size of modulation
L = 1; % Length of impulse response of channel
msg = [0:M-1 0]; % M-ary message sequence of length > M^L

% Step 2. Modulate the message signal using baseband modulation.
%hMod = comm.RectangularQAMModulator(M);  % Use 16-QAM.
%modsig = step(hMod,msg'); % Modulate data
modsig = qammod(msg',M); % Modulate data
Nsamp = 16;
modsig = rectpulse(modsig,Nsamp); % Use rectangular pulse shaping.

% Step 3. Apply a transmit filter.
txsig = modsig; % No filter in this example

% Step 4. Run txsig through a noiseless channel.
rxsig = txsig*exp(1i*pi/180); % Static phase offset of 1 degree
% Step 5. Use the semianalytic function.
% Specify the receive filter as a pair of input arguments.
% In this case, num and den describe an ideal integrator.
num = ones(Nsamp,1)/Nsamp;
den = 1;
EbNo = 0:20; % Range of Eb/No values under study
ber = semianalytic(txsig,rxsig,'qam',M,Nsamp,num,den,EbNo);

% For comparison, calculate theoretical BER.
bertheory = berawgn(EbNo,'qam',M);

% Plot computed BER and theoretical BER.
figure; semilogy(EbNo,ber,'k*');
hold on; semilogy(EbNo,bertheory,'ro');
title('Semianalytic BER Compared with Theoretical BER');
legend('Semianalytic BER with Phase Offset',...
   'Theoretical BER Without Phase Offset','Location','SouthWest');
hold off;

Этот пример создает фигуру как та ниже.

Теоретические результаты производительности

Вычисление теоретической ошибочной статистики
Графический вывод теоретических коэффициентов ошибок
Сравнение теоретических и эмпирических коэффициентов ошибок

Вычисление теоретической ошибочной статистики

В то время как функция biterr, обсужденная выше, может помочь вам собрать эмпирическую ошибочную статистику, вы можете также сравнить те результаты с теоретической ошибочной статистикой. Определенные типы систем связи сопоставлены с выражениями закрытой формы для частоты ошибок по битам или привязанного это. Функции, перечисленные в таблице ниже, вычисляют выражения закрытой формы для некоторых типов систем связи, где такие выражения существуют.

Тип системы связи	Функция
Незакодированный канал AWGN	`berawgn`
Закодированный канал AWGN	`bercoding`
Незакодированный Rayleigh и Rician, исчезающий канал	`berfading`
Незакодированные AWGN образовывают канал с несовершенной синхронизацией	`bersync`

Страница с описанием каждой функции перечисляет одну или несколько книг, содержащих выражения закрытой формы, которые реализует функция.

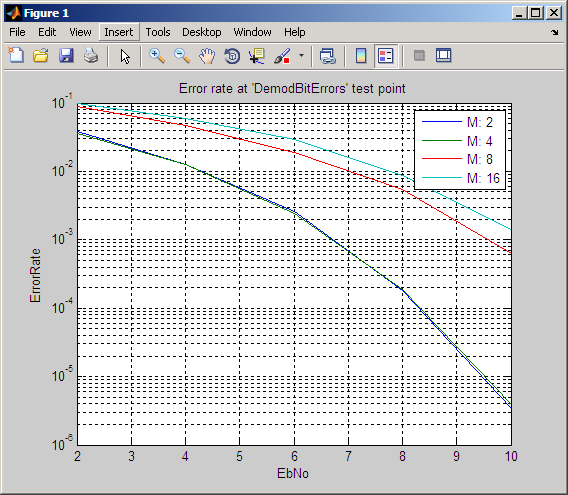
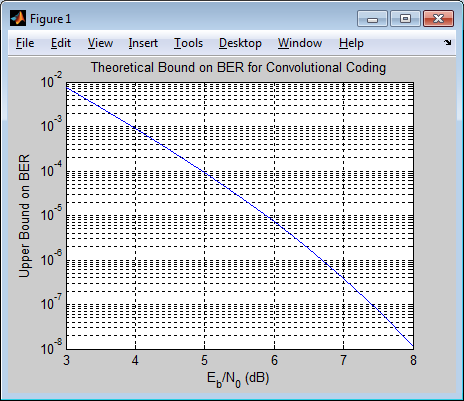
Графический вывод теоретических коэффициентов ошибок

Пример ниже использует функцию bercoding, чтобы вычислить верхние границы на частотах ошибок по битам для сверточного кодирования с декодером мягкого решения. Данные, используемые для генератора и спектра расстояния, от [1] и [12], соответственно.

coderate = 1/4; % Code rate
% Create a structure dspec with information about distance spectrum.
dspec.dfree = 10; % Minimum free distance of code
dspec.weight = [1 0 4 0 12 0 32 0 80 0 192 0 448 0 1024 ...
   0 2304 0 5120 0]; % Distance spectrum of code
EbNo = 3:0.5:8;
berbound = bercoding(EbNo,'conv','soft',coderate,dspec);
semilogy(EbNo,berbound) % Plot the results.
xlabel('E_b/N_0 (dB)'); ylabel('Upper Bound on BER');
title('Theoretical Bound on BER for Convolutional Coding');
grid on;

Этот пример производит следующий график.

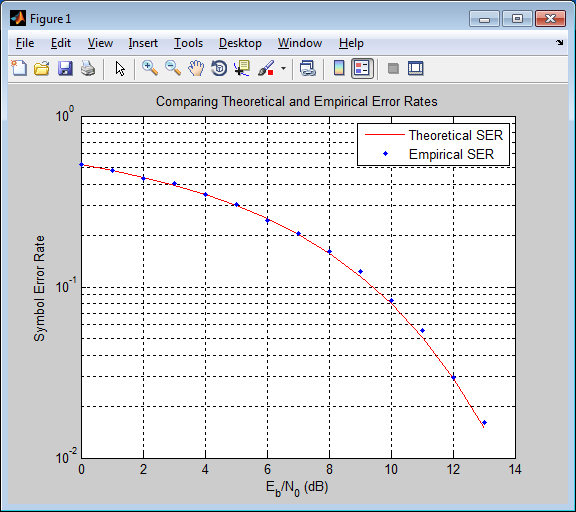
Сравнение теоретических и эмпирических коэффициентов ошибок

Пример ниже использует функцию berawgn, чтобы вычислить коэффициенты ошибок символа для импульсной амплитудной модуляции (PAM) с серией значений _Eb/N0. Для сравнения код моделирует 8-PAM с каналом AWGN и вычисляет эмпирические коэффициенты ошибок символа. Код также строит теоретические и эмпирические коэффициенты ошибок символа того же набора осей.

% 1. Compute theoretical error rate using BERAWGN.
rng('default')      % Set random number seed for repeatability
%
M = 8; EbNo = 0:13;
[ber, ser] = berawgn(EbNo,'pam',M);
% Plot theoretical results.
figure; semilogy(EbNo,ser,'r');
xlabel('E_b/N_0 (dB)'); ylabel('Symbol Error Rate');
grid on; drawnow;

% 2. Compute empirical error rate by simulating.
% Set up.
n = 10000; % Number of symbols to process
k = log2(M); % Number of bits per symbol
% Convert from EbNo to SNR.
% Note: Because No = 2*noiseVariance^2, we must add 3 dB
% to get SNR. For details, see Proakis' book listed in
% "Selected Bibliography for Performance Evaluation."
snr = EbNo+3+10*log10(k);
% Preallocate variables to save time.
ynoisy = zeros(n,length(snr));
z      = zeros(n,length(snr));
berVec = zeros(3,length(EbNo));

% PAM modulation and demodulation system objects
%h  = comm.PAMModulator(M);
%h2 = comm.PAMDemodulator(M);

% AWGNChannel System object
hChan = comm.AWGNChannel('NoiseMethod', 'Signal to noise ratio (SNR)');


% ErrorRate calculator System object to compare decoded symbols to the
% original transmitted symbols.
hErrorCalc = comm.ErrorRate;

% Main steps in the simulation
x = randi([0 M-1],n,1); % Create message signal.
%y = step(h,x); % Modulate.
y = pammod(x,M); % Modulate.
hChan.SignalPower = (real(y)' * real(y))/ length(real(y));

% Loop over different SNR values.
for jj = 1:length(snr)
    reset(hErrorCalc)
    hChan.SNR = snr(jj); % Assign Channel SNR
    ynoisy(:,jj) = step(hChan,real(y)); % Add AWGN
%    z(:,jj) = step(h2,complex(ynoisy(:,jj))); % Demodulate.
    z(:,jj) = pamdemod(complex(ynoisy(:,jj)),M); % Demodulate.

    % Compute symbol error rate from simulation.
    berVec(:,jj) = step(hErrorCalc, x, z(:,jj));
end

% 3. Plot empirical results, in same figure.
hold on; semilogy(EbNo,berVec(1,:),'b.');
legend('Theoretical SER','Empirical SER');
title('Comparing Theoretical and Empirical Error Rates');
hold off;

Этот пример производит график как тот в следующей фигуре. Ваш график может отличаться, потому что симуляция использует случайные числа.

Графики коэффициента ошибок

Разделите обзор
Создание графиков коэффициента ошибок Используя semilogy
Curve Fitting для графиков коэффициента ошибок
Пример: Curve Fitting для графика коэффициента ошибок

Разделите обзор

Графики коэффициента ошибок обеспечивают визуальный способ исследовать производительность системы связи, и они часто включаются в публикации. Этот раздел упоминает некоторые инструменты, которые можно использовать, чтобы создать графики коэффициента ошибок, изменить их, чтобы удовлетворить потребностям и сделать аппроксимирование кривыми на данных о коэффициенте ошибок. Это также обеспечивает пример аппроксимирования кривыми. Для более детальных обсуждений о более общих возможностях графического вывода в MATLAB^® смотрите набор документации MATLAB.

Создание графиков коэффициента ошибок Используя `semilogy`

Во многих графиках коэффициента ошибок горизонтальная ось указывает на значения _Eb/N0 в дБ, и вертикальная ось указывает на коэффициент ошибок с помощью логарифмического (базируйтесь 10), шкала. Чтобы видеть пример такого графика, а также кода, который создает его, смотрите Сравнение Теоретических и Эмпирических Коэффициентов ошибок. Часть того примера, который создает график, использует функцию semilogy, чтобы произвести логарифмический масштаб на вертикальной оси и линейную шкалу на горизонтальной оси.

Другие примеры, которые иллюстрируют использование semilogy, находятся в этих разделах:

Пример: Используя Полуаналитический Метод, который также иллюстрирует
- Графический вывод двух наборов данных по одной паре осей
- Добавление заголовка
- Добавление легенды
Графический вывод Теоретических Коэффициентов ошибок, который также иллюстрирует
- Добавление подписей по осям
- Добавление линий сетки

Curve Fitting для графиков коэффициента ошибок

Аппроксимирование кривыми полезно, когда вы имеете небольшой или несовершенный набор данных, но хотите построить плавную кривую в целях представления. Функция berfit в Communications Toolbox предлагает возможности подбора кривых, которые хорошо подходят для ситуации, когда эмпирические данные описывают коэффициенты ошибок в различных значениях _Eb/N0. Эта функция позволяет

Настройте различные соответствующие аспекты процесса подбора кривых, такие как тип функции закрытой формы (из списка предварительно установленного выбора) раньше генерировал подгонку.
Отобразите эмпирические данные на графике наряду с кривой, которой berfit соответствует к данным.
Интерполируйте точки на кривой по экспериментальным точкам между значениями _Eb/N0 в вашем наборе эмпирических данных, чтобы сделать график более сглаженным взглядом.
Соберите релевантную информацию о подгонке, такой как численные значения точек вдоль кривой по экспериментальным точкам и коэффициентов подходящего выражения.

Примечание

Функция berfit предназначается для аппроксимирования кривыми или интерполяции, не экстраполяции. Экстраполирование данных о BER вне порядка величины ниже наименьшего эмпирического значения BER по сути ненадежно.

Для полного списка вводов и выводов для berfit смотрите его страницу с описанием.

Пример: Curve Fitting для графика коэффициента ошибок

Этот пример моделирует простой DBPSK (дифференциальное бинарное манипулирование сдвига фазы) система связи и отображает данные о коэффициенте ошибок на графике для серии значений _Eb/N0. Это использует функцию berfit, чтобы соответствовать кривой к несколько грубому набору эмпирических коэффициентов ошибок. Поскольку пример долог, это обсуждение представляет его на нескольких шагах:

Подготовка параметров для симуляции
Симуляция системы Используя цикл
Графический вывод эмпирических результатов и кривой по экспериментальным точкам

Подготовка Параметров для Симуляции. Первый шаг в примере настраивает параметры, которые будут использоваться во время симуляции. Параметры включают область значений значений _Eb/N0, чтобы рассмотреть и минимальное количество ошибок, которые должны произойти, прежде чем симуляция вычисляет коэффициент ошибок для этого значение _Eb/N0.

Примечание

Для большинства приложений необходимо основывать вычисление коэффициента ошибок на большем числе ошибок, чем используется здесь (например, вы можете изменить numerrmin на 100 в коде ниже). Однако этот пример использует небольшое количество ошибок просто, чтобы проиллюстрировать, как аппроксимирование кривыми может сгладить грубый набор данных.

% Set up initial parameters.
siglen = 100000; % Number of bits in each trial
M = 2; % DBPSK is binary.
% DBPSK modulation and demodulation System objects
hMod  = comm.DBPSKModulator;
hDemod = comm.DBPSKDemodulator;
% AWGNChannel System object
hChan = comm.AWGNChannel('NoiseMethod', 'Signal to noise ratio (SNR)');
% ErrorRate calculator System object to compare decoded symbols to the
% original transmitted symbols.
hErrorCalc = comm.ErrorRate;
EbNomin = 0; EbNomax = 9; % EbNo range, in dB
numerrmin = 5; % Compute BER only after 5 errors occur.
EbNovec = EbNomin:1:EbNomax; % Vector of EbNo values
numEbNos = length(EbNovec); % Number of EbNo values
% Preallocate space for certain data.
ber = zeros(1,numEbNos); % final BER values
berVec = zeros(3,numEbNos); % Updated BER values
intv = cell(1,numEbNos); % Cell array of confidence intervals

Симуляция Системы Используя Цикл. Следующий шаг в примере должен использовать цикл for, чтобы отличаться значение _Eb/N0 (обозначенный EbNo в коде) и моделировать систему связи для каждого значения. Внутренний цикл while гарантирует, что симуляция продолжает использовать данное значение EbNo до, по крайней мере, предопределенное минимальное количество ошибок произошло. Когда система является очень шумной, это требует только одной передачи через цикл while, но в других случаях, это требует нескольких передач.

Симуляция системы связи использует эти функции тулбокса:

randi, чтобы сгенерировать случайную последовательность сообщения
dpskmod, чтобы выполнить модуляцию DBPSK
awgn, чтобы смоделировать канал с аддитивным белым Гауссовым шумом
dpskdemod, чтобы выполнить демодуляцию DBPSK
biterr, чтобы вычислить количество ошибок для данного проходит через цикл while
berconfint, чтобы вычислить уровень конечной погрешности и доверительный интервал для данного значения EbNo

В то время как пример прогрессирует через цикл for, он собирает данные для дальнейшего использования в аппроксимировании кривыми и графическом выводе:

ber, вектор, содержащий частоты ошибок по битам для серии значений EbNo.
intv, массив ячеек, содержащий доверительные интервалы для серии значений EbNo. Каждая запись в intv является двухэлементным вектором, который дает конечные точки интервала.

% Loop over the vector of EbNo values.
berVec = zeros(3,numEbNos); % Reset
for jj = 1:numEbNos
    EbNo = EbNovec(jj);
    snr = EbNo; % Because of binary modulation
    reset(hErrorCalc)
    hChan.SNR = snr; % Assign Channel SNR
    % Simulate until numerrmin errors occur.
    while (berVec(2,jj) < numerrmin)
        msg = randi([0,M-1], siglen, 1); % Generate message sequence.
        txsig = step(hMod, msg); % Modulate.
        hChan.SignalPower = (txsig'*txsig)/length(txsig);  % Calculate and
        % assign signal power
        rxsig = step(hChan,txsig); % Add noise.
        decodmsg = step(hDemod, rxsig); % Demodulate.
        if (berVec(2,jj)==0)
            % The first symbol of a differentially encoded transmission
            % is discarded.
            berVec(:,jj) = step(hErrorCalc, msg(2:end),decodmsg(2:end));
        else
            berVec(:,jj) = step(hErrorCalc, msg, decodmsg);
        end
    end
    % Error rate and 98% confidence interval for this EbNo value
    [ber(jj), intv1] = berconfint(berVec(2,jj),berVec(3,jj)-1,.98);
    intv{jj} = intv1; % Store in cell array for later use.
    disp(['EbNo = ' num2str(EbNo) ' dB, ' num2str(berVec(2,jj)) ...
        ' errors, BER = ' num2str(ber(jj))])
end

Эта часть примера отображает вывод в Командном окне, в то время как это прогрессирует через цикл for. Ваш точный вывод может отличаться, потому что этот пример использует случайные числа.

EbNo = 0 dB, 189 errors, BER = 0.18919
EbNo = 1 dB, 139 errors, BER = 0.13914
EbNo = 2 dB, 105 errors, BER = 0.10511
EbNo = 3 dB, 66 errors, BER = 0.066066
EbNo = 4 dB, 40 errors, BER = 0.04004
EbNo = 5 dB, 18 errors, BER = 0.018018
EbNo = 6 dB, 6 errors, BER = 0.006006
EbNo = 7 dB, 11 errors, BER = 0.0055028
EbNo = 8 dB, 5 errors, BER = 0.00071439
EbNo = 9 dB, 5 errors, BER = 0.00022728
EbNo = 10 dB, 5 errors, BER = 1.006e-005

Графический вывод эмпирических результатов и кривой по экспериментальным точкам

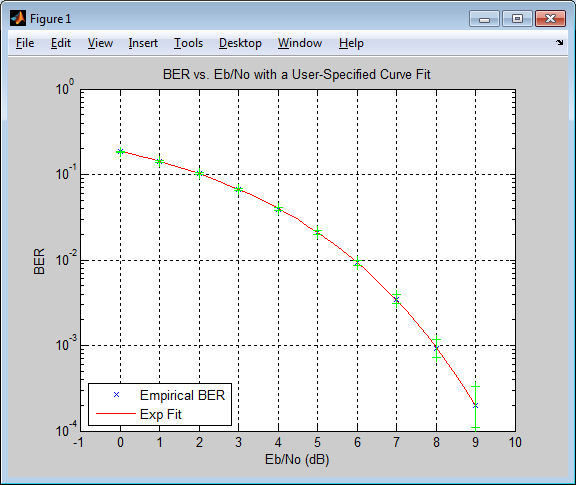
Итоговая часть этого примера соответствует кривой к данным о BER, собранным от цикла симуляции. Это также строит значение погрешности с помощью вывода от функции berconfint.

% Use BERFIT to plot the best fitted curve,
% interpolating to get a smooth plot.
fitEbNo = EbNomin:0.25:EbNomax; % Interpolation values
berfit(EbNovec,ber,fitEbNo,[],'exp');

% Also plot confidence intervals.
hold on;
for jj=1:numEbNos
   semilogy([EbNovec(jj) EbNovec(jj)],intv{jj},'g-+');
end
hold off;

BERTool

Команда bertool запускает Аналитический Инструмент Частоты ошибок по битам (BERTool) приложение.

Приложение позволяет вам анализировать производительность частоты ошибок по битам (BER) систем связи. BERTool вычисляет BER как функцию отношения сигнал-шум. Это анализирует производительность или с симуляциями Монте-Карло функций MATLAB и моделей Simulink^® или с теоретическими выражениями закрытой формы для выбранных типов систем связи.

Используя BERTool вы можете:

Сгенерируйте данные о BER для использования системы связи
- Выражения закрытой формы для теоретической производительности BER выбранных типов систем связи.
- Полуаналитический метод.
- Симуляции содержатся в функциях симуляции MATLAB или моделях Simulink. После того, как вы создаете функцию или модель, которая моделирует систему, BERTool выполняет итерации по вашему выбору значений _Eb/N0 и собирает результаты.
Постройте один или несколько наборов данных BER на одном наборе осей. Например, можно графически сравнить данные моделирования с теоретическими результатами или данные моделирования от ряда подобных моделей системы связи.
Соответствуйте кривой к набору данных моделирования.
Отправьте данные о BER в рабочее пространство MATLAB, или в файл для дальнейшей обработки вас может хотеть выполнить.

Примечание

BERTool разработан для анализа частот ошибок по битам только, не коэффициентов ошибок символа, коэффициентов ошибок слова или других типов коэффициентов ошибок. Если, например, ваша симуляция вычисляет коэффициент ошибок символа (SER), преобразуйте SER в BER перед использованием симуляции с BERTool.

Следующие разделы описывают Аналитический Инструмент Частоты ошибок по битам (BERTool) и обеспечивают примеры, показывающие, как использовать его графический интерфейс пользователя.

Запустите BERTool
Среда BERTool
Вычисление теоретического BERs
Используя полуаналитический метод, чтобы вычислить BERs
Запустите симуляции MATLAB
Используйте функции симуляции с BERTool
Запустите симуляции Simulink
Используйте модели Simulink с BERTool
Управляйте данными о BER

Запустите BERTool

Чтобы открыть BERTool, ввести

bertool

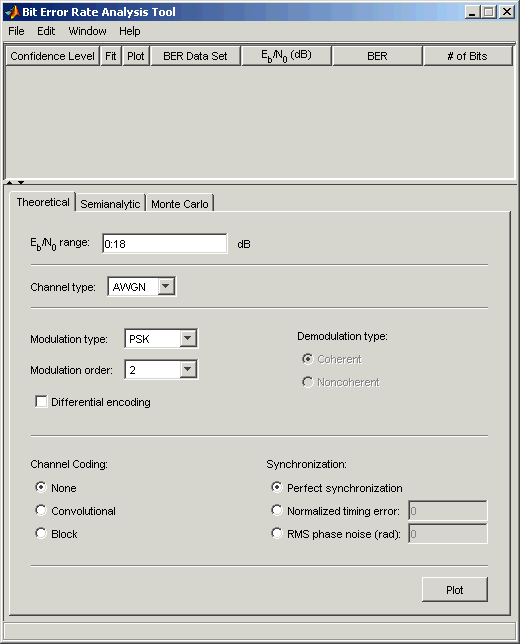
Компоненты BERTool

Средство просмотра данных наверху. Это первоначально пусто.
После того, как вы дадите BERTool команду генерировать один или несколько наборов данных BER, они появляются в средстве просмотра данных. Пример, который показывает, как взгляд наборов данных в средстве просмотра данных находится в Примере: Используя Симуляцию MATLAB с BERTool.
Набор вкладок на нижней части. Маркировал Theoretical, Semianalytic и Monte Carlo, вкладки соответствуют различным методам, которыми BERTool может сгенерировать данные о BER.

Примечание
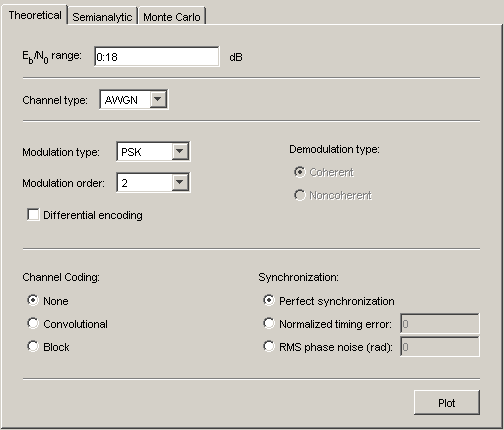
При использовании BERTool, чтобы сравнить теоретические результаты и результаты Монте-Карло, предоставленная модель Simulink должна смоделировать точно систему, заданную параметрами на вкладке Theoretical.
Чтобы узнать больше о каждом из методов, смотрите
Отдельное Окно рисунка BER, которое отображает некоторых или все наборы данных BER, которые перечислены в средстве просмотра данных. BERTool создает Окно фигуры BER после того, как это имеет по крайней мере один набор данных, чтобы отобразиться, таким образом, вы не видите Окно рисунка BER, когда вы сначала открываете BERTool. Для примера того, как Окно рисунка BER выглядит, смотрите Пример: Используя Теоретическую Вкладку в BERTool.

Взаимодействие Среди Компонентов BERTool. Компоненты BERTool действуют как один интегрированный инструмент. Эти поведения отражают свое интегрирование:

Если вы выбираете набор данных в средстве просмотра данных, BERTool реконфигурировал вкладки, чтобы отразить параметры, сопоставленные с тем набором данных, и также подсвечивает соответствующие данные в Окне рисунка BER. Это полезно, если средство просмотра данных отображает несколько наборов данных, и вы хотите вспомнить значение и источник каждого набора данных.
Если вы кликаете по данным, отображенным на графике в Окне рисунка BER, BERTool реконфигурировал вкладки, чтобы отразить параметры, сопоставленные с теми данными, и также подсвечивает соответствующий набор данных в средстве просмотра данных.

Примечание
Вы не можете нажать на точку данных, в то время как BERTool генерирует результаты симуляции Монте-Карло. Необходимо ожидать, пока инструмент не генерирует все точки данных прежде, чем щелкнуть для получения дополнительной информации.
Если вы конфигурируете вкладку Semianalytic или Theoretical способом, которая уже отражается в существующем наборе данных, BERTool подсвечивает что набор данных в средстве просмотра данных. Это препятствует тому, чтобы BERTool копировал свои вычисления и свои записи в средстве просмотра данных, все еще показывая вам результаты, которые вы запросили.
Если вы закрываете Окно рисунка BER, то можно вновь открыть его путем выбора BER Figure из меню Window в BERTool.
Если вы выбираете опции в средстве просмотра данных, которые влияют на график BER, Окно рисунка BER сразу отражает ваши выборы. Такие опции относятся к именам набора данных, доверительным интервалам, аппроксимированию кривыми, и присутствию или отсутствию определенных наборов данных в графике BER.

Примечание

Если вы хотите наблюдать интегрирование сами, но еще не имеете никаких наборов данных в BERTool, то сначала пробуют процедуру в Примере: Используя Теоретическую Вкладку в BERTool.

Примечание

Если вы сохраняете Окно рисунка BER с помощью меню File окна, получившийся файл содержит содержимое окна, но не данных BERTool, которые привели к графику. Чтобы сохранить целый сеанс BERTool, смотрите Сохранение Сеанса BERTool.

Вычисление теоретического BERs

Разделите обзор
Пример: Используя теоретическую вкладку в BERTool
Доступные наборы теоретических данных о BER

Разделите Обзор. Можно использовать BERTool, чтобы сгенерировать и анализировать теоретические данные о BER. Теоретические данные полезны для сравнения с вашими результатами симуляции. Однако выражения BER закрытой формы существуют только для определенных видов систем связи.

Чтобы получить доступ к возможностям BERTool, связанного с теоретическими данными о BER, используйте следующую процедуру:

Откройте BERTool и перейдите к вкладке Theoretical.
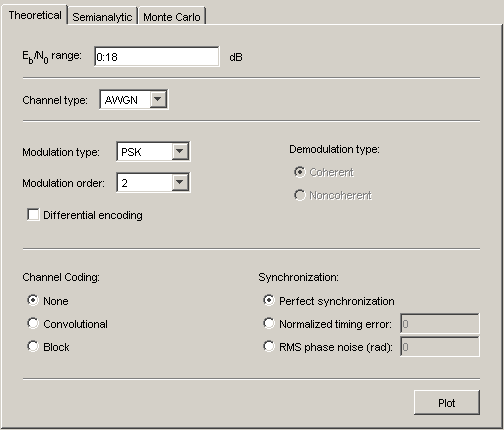
Установите параметры, чтобы отразить систему, производительность которой вы хотите анализировать. Некоторые параметры видимы и активны только, когда другие параметры имеют определенные значения. Смотрите Доступные Наборы Теоретических Данных о BER для деталей.
Нажмите Plot.

Для примера, который показывает, как сгенерировать и анализировать теоретические данные о BER через BERTool, смотрите Пример: Используя Теоретическую Вкладку в BERTool.

Кроме того, Доступные Наборы Теоретических Данных о BER указывает, какие комбинации параметров доступны на вкладке Theoretical и какие базовые функции выполняют вычисления.

Пример: Используя Теоретическую Вкладку в BERTool. Этот пример иллюстрирует, как использовать BERTool, чтобы сгенерировать и отобразить теоретические данные о BER на графике. В частности, пример сравнивает производительность системы связи, которая использует канал AWGN и модуляцию QAM различных порядков.

Выполнение теоретического примера

Откройте BERTool и перейдите к вкладке Theoretical.
Установите параметры как показано в следующей фигуре.
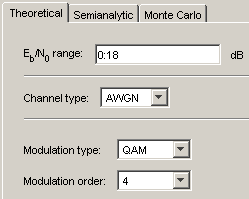
Нажмите Plot.
BERTool создает запись в средстве просмотра данных и отображает данные на графике в Окне рисунка BER. Даже при том, что параметры запрашивают, чтобы _Eb/N0 подошли 18, BERTool строит только те значения BER, которые являются ^{по крайней мере 10-8}. Следующие фигуры иллюстрируют этот шаг.
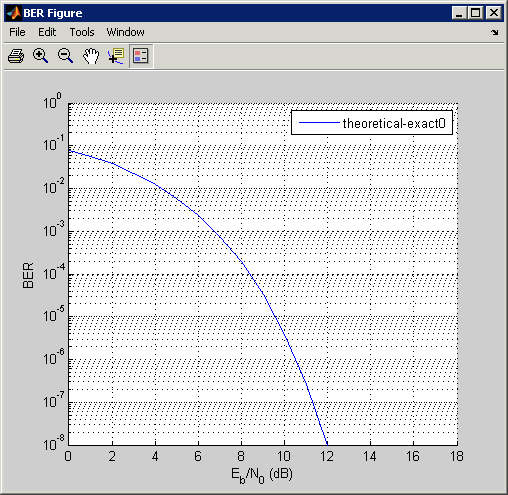
Измените параметр Modulation order на 16 и нажмите Plot.
BERTool создает другую запись в средстве просмотра данных и отображает новые данные на графике в том же Окне рисунка BER (не изображенный).
Измените параметр Modulation order на 64 и нажмите Plot.
BERTool создает другую запись в средстве просмотра данных и отображает новые данные на графике в том же Окне рисунка BER, как показано в следующих фигурах.
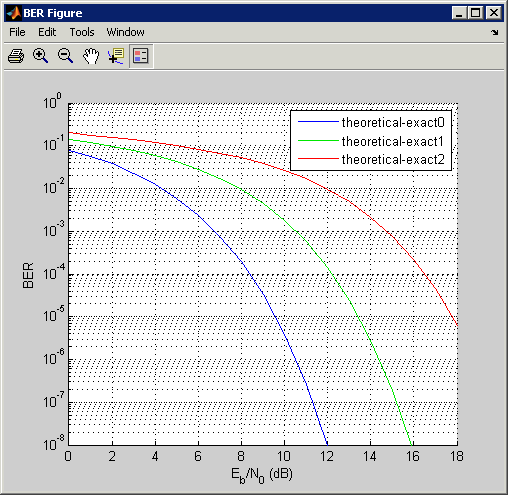
Чтобы вспомнить, какое значение Modulation order соответствует данной кривой, кликните по кривой. BERTool отвечает путем корректировки параметров во вкладке Theoretical, чтобы отразить значения, которые соответствуют той кривой.
Чтобы удалить последнюю кривую из графика (но не из средства просмотра данных), снимите флажок в последней записи средства просмотра данных в столбце Plot. Чтобы восстановить кривую к графику, установите флажок снова.

Доступные Наборы Теоретических Данных о BER. BERTool может сгенерировать большой набор теоретических частот ошибок по битам, но не все комбинации параметров в настоящее время поддержаны. Вкладка Theoretical настраивает себя к вашему выбору, так, чтобы комбинация параметров была всегда допустима. Можно установить параметр Modulation order путем выбора выбора из меню или путем ввода значения в поле. Normalized timing error должен быть между 0 и 0.5.

BERTool принимает, что Грэй, кодирующий, используется для всех модуляций.

Для QAM, когда ${журнал}_{2} M$ нечетно (M, являющийся порядком модуляции), прямоугольная совокупность принята.

Комбинации параметров для систем канала AWGN

В следующей таблице перечислены доступные наборы теоретических данных о BER для систем, которые используют канал AWGN.

Модуляция	Порядок модуляции	Другой выбор
PSK	2, 4	Дифференциальное или недифференциальное кодирование.
PSK	8, 16, 32, 64, или более высокая степень 2
OQPSK	4	Дифференциальное или недифференциальное кодирование.
DPSK	2, 4, 8, 16, 32, 64, или более высокая степень 2
PAM	2, 4, 8, 16, 32, 64, или более высокая степень 2
QAM	4, 8, 16, 32, 64, 128, 256, 512, 1024, или более высокая степень 2
FSK	2	Ортогональный или неортогональный; `Coherent` или демодуляция `Noncoherent`.
	4, 8, 16, 32, или более высокая степень 2	Ортогональный; демодуляция `Coherent`.
	4, 8, 16, 32, или 64	Ортогональный; демодуляция `Noncoherent`.
MSK	2	`Coherent` обычный или предварительно закодированный MSK; `Noncoherent` предварительно закодировал MSK.
CPFSK	2, 4, 8, 16, или более высокая степень 2	`Modulation index`> 0.

Результаты BER также доступны для следующего:

блокируйтесь и сверточное кодирование с декодированием трудного решения для всех модуляций кроме CPFSK
блочное кодирование с декодированием мягкого решения для всех двоичных модуляций (включая 4-PSK и 4-QAM) кроме CPFSK, некогерентного неортогонального FSK и некогерентного MSK
сверточное кодирование с декодированием мягкого решения для всех двоичных модуляций (включая 4-PSK и 4-QAM) кроме CPFSK
незакодированный недифференцированно закодированный 2-PSK с ошибками синхронизации

Для получения дополнительной информации об определенных комбинациях параметров, включая библиографические ссылки, которые содержат выражения закрытой формы, смотрите страницы с описанием для следующих функций:

berawgn — Для систем без кодирования и совершенной синхронизации
bercoding — Для систем с кодированием канала
bersync — Для систем с модуляцией BPSK, никаким кодированием и несовершенной синхронизацией

Комбинации параметров для рэлеевского и систем канала Rician

В следующей таблице перечислены доступные наборы теоретических данных о BER для систем, которые используют канал Rayleigh или Rician.

Когда разнообразие используется, ОСШ на каждом ответвлении разнообразия выведен от ОСШ во входе канала (EbNo), разделенный на порядок разнообразия.

Модуляция	Порядок модуляции	Другой выбор
PSK	2	Дифференциальное или недифференциальное кодирование `Diversity order` ≧1 В случае недифференциального кодирования, порядок разнообразия, являющийся 1, и исчезновение Rician, может быть задано значение для шума фазы RMS (в радианах).
PSK	4, 8, 16, 32, 64, или более высокая степень 2	`Diversity order` ≧1
OQPSK	4	`Diversity order` ≧1
DPSK	2, 4, 8, 16, 32, 64, или более высокая степень 2	`Diversity order` ≧1
PAM	2, 4, 8, 16, 32, 64, или более высокая степень 2	`Diversity order` ≧1
QAM	4, 8, 16, 32, 64, 128, 256, 512, 1024, или более высокая степень 2	`Diversity order` ≧1
FSK	2	Коэффициент корреляции $\in [- 1, 1]$ . `Coherent` или демодуляция `Noncoherent` `Diversity order` ≧1 В случае ненулевого коэффициента корреляции и некогерентной демодуляции, порядок разнообразия равняется 1 только.
FSK	4, 8, 16, 32, или более высокая степень 2	Демодуляция `Noncoherent` только. `Diversity order` ≧1

Для получения дополнительной информации об определенных комбинациях параметров, включая библиографические ссылки, которые содержат выражения закрытой формы, смотрите страницу с описанием для функции berfading.

Используя полуаналитический метод, чтобы вычислить BERs

Разделите обзор
Пример: Используя полуаналитическую вкладку в BERTool
Процедура для Использования полуаналитической вкладки в BERTool

Разделите Обзор. Можно использовать BERTool, чтобы сгенерировать и анализировать данные о BER через полуаналитический метод. Полуаналитический метод обсужден в Результатах Производительности через Полуаналитический Метод, и Когда Использовать Полуаналитический Метод, особенно релевантно как справочный материал.

Чтобы получить доступ к полуаналитическим возможностям BERTool, откройте вкладку Semianalytic.

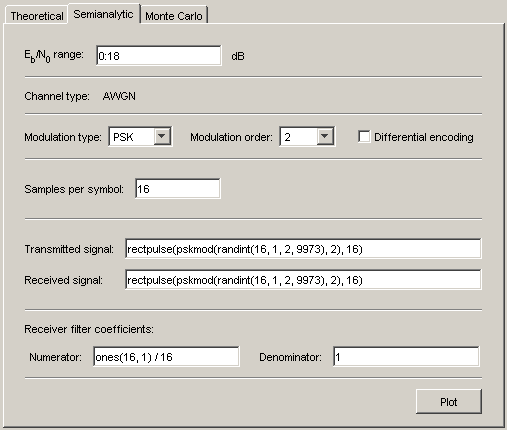
Для получения дальнейшей информации о том, как BERTool применяет полуаналитический метод, смотрите страницу с описанием для функции semianalytic, который использование BERTool выполнить вычисления.

Пример: Используя Полуаналитическую Вкладку в BERTool. Этот пример иллюстрирует, как BERTool применяет полуаналитический метод, с помощью 16-QAM модуляции. Этим примером является изменение на примере в Примере: Используя Полуаналитический Метод, но это адаптируется, чтобы использовать BERTool вместо того, чтобы использовать функцию semianalytic непосредственно.

Выполнение полуаналитического примера

Чтобы настроить переданные и полученные сигналы, запустите шаги 1 - 4 от примера кода в Примере: Используя Полуаналитический Метод. Код повторяется ниже.

% Step 1. Generate message signal of length >= M^L.
M = 16; % Alphabet size of modulation
L = 1; % Length of impulse response of channel
msg = [0:M-1 0]; % M-ary message sequence of length > M^L

% Step 2. Modulate the message signal using baseband modulation.
%hMod = comm.RectangularQAMModulator(M);  % Use 16-QAM.
%modsig = step(hMod,msg'); % Modulate data
modsig = qammod(msg',M); % Modulate data
Nsamp = 16;
modsig = rectpulse(modsig,Nsamp); % Use rectangular pulse shaping.

% Step 3. Apply a transmit filter.
txsig = modsig; % No filter in this example

% Step 4. Run txsig through a noiseless channel.
rxsig = txsig*exp(1i*pi/180); % Static phase offset of 1 degree

Откройте BERTool и перейдите к вкладке Semianalytic.
Установите параметры как показано в следующей фигуре.
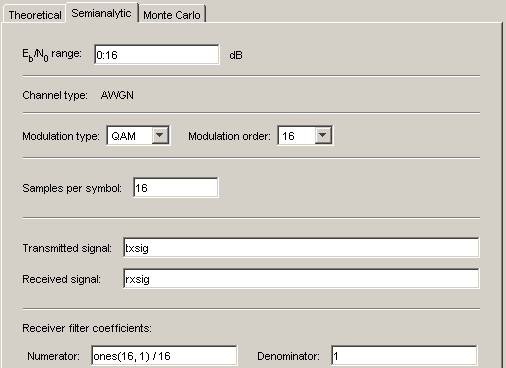
Нажмите Plot.

Видимые результаты полуаналитического примера

После того, как вы нажмете Plot, BERTool создает листинг для получившихся данных в средстве просмотра данных.

BERTool отображает данные на графике в Окне рисунка BER.

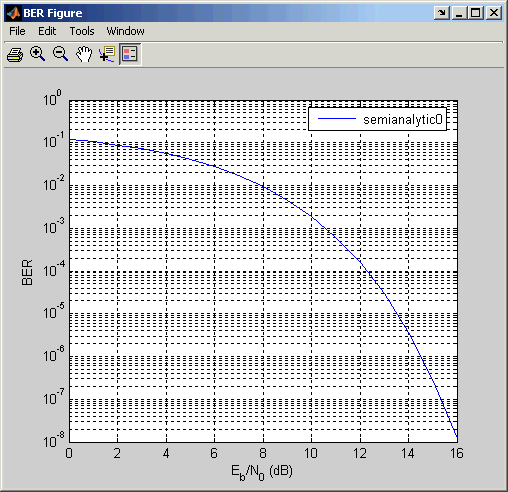
Процедура для Использования Полуаналитической Вкладки в BERTool. Процедура ниже описывает, как вы обычно реализуете полуаналитический метод с помощью BERTool:

Сгенерируйте сигнал сообщения, содержащий, по крайней мере, символы ^ML, где M является размером алфавита модуляции, и L является продолжительностью импульсного ответа канала в символах. Общий подход должен запустить с увеличенного бинарного псевдошума (PN) последовательность общей длины _(log2M)ML. Увеличенная последовательность PN является последовательностью PN с дополнительным добавленным нулем, который делает распределение единиц и нулей равным.
Модулируйте поставщика услуг с сигналом сообщения использование основополосной модуляции. Поддерживаемые типы модуляции перечислены на странице с описанием для semianalytic. Сформируйте результирующий сигнал с формированием меандра, с помощью фактора сверхдискретизации, что вы будете дальнейшее использование, чтобы отфильтровать модулируемый сигнал. Сохраните результат этого шага как txsig для дальнейшего использования.
Отфильтруйте модулируемый сигнал с фильтром передачи. Этот фильтр часто является повышенным фильтром косинуса квадратного корня, но можно также использовать Баттерворта, функцию Бесселя, Чебышевский тип 1 или 2, эллиптического, или более общего КИХ или БИХ-фильтр. Если вы используете повышенный фильтр косинуса квадратного корня, используйте его на несверхдискретизированном модулируемом сигнале и укажите, что сверхдискретизация включает функцию фильтрации. Если вы используете другой тип фильтра, можно применить его к rectangularly сигналу импульсной формы.
Запустите пропущенный сигнал через бесшумный канал. Этот канал может включать многопутевые исчезающие эффекты, сдвиги фазы, нелинейность усилителя, квантование и дополнительную фильтрацию, но это не должно включать шум. Сохраните результат этого шага как rxsig для дальнейшего использования.

На вкладке Semianalytic BERTool введите параметры как в приведенную ниже таблицу.

'ParameterName'	Значение
Eb/No range	Вектор, который перечисляет значения _Eb/N0, для которого вы хотите собрать данные о BER. Значение в этом поле может быть выражением MATLAB или именем переменной в рабочем пространстве MATLAB.
Modulation type	Эти параметры описывают схему модуляции, которую вы использовали ранее в этой процедуре.
Modulation order
Differential encoding	Этот флажок, который видим и активен для MSK и модуляции PSK, позволяет вам выбрать между дифференциальным и недифференциальным кодированием.
Samples per symbol	Количество выборок на символ в переданном сигнале. Это значение является также уровнем выборки переданных и полученных сигналов в Гц.
Transmitted signal	Сигнал `txsig`, что вы сгенерировали ранее в этой процедуре
Received signal	Сигнал `rxsig`, что вы сгенерировали ранее в этой процедуре
Numerator	Коэффициенты фильтра получателя, что BERTool применяется к полученному сигналу
Denominator

Примечание

Непротиворечивость среди значений в графический интерфейсе пользователя важна. Например, если сигнал, на который ссылаются в поле Transmitted signal, был сгенерирован с помощью DPSK, и вы устанавливаете Modulation type на MSK, результаты не могут быть значимыми.

Нажмите Plot.

Полуаналитические вычисления и результаты

После того, как вы нажмете Plot, BERTool выполняет эти задачи:

Фильтры rxsig и затем определяют вероятность появления ошибки каждого полученного очка сигнала путем аналитичного применения Гауссова шумового распределения к каждой точке. BERTool составляет в среднем вероятности появления ошибки по целому полученному сигналу определить полную вероятность появления ошибки. Если вероятность появления ошибки, вычисленная таким образом, является вероятностью появления ошибки символа, BERTool преобразовывает ее в небольшой коэффициент ошибок, обычно путем принятия Грэя, кодирующего. (Если тип модуляции является DQPSK или перекрестным QAM, результатом является верхняя граница на частоте ошибок по битам, а не самой частоте ошибок по битам.)
Вводит получившиеся данные о BER в средство просмотра данных окна BERTool.
Отображает получившиеся данные о BER на графике в Окне рисунка BER.

Запустите симуляции MATLAB

Разделите обзор
Пример: Используя симуляцию MATLAB с BERTool
Отличаясь критерий остановки
Графический вывод доверительных интервалов
Подходящий BER указывает на кривую

Разделите Обзор. Можно использовать BERTool в сочетании с собственными функциями симуляции MATLAB, чтобы сгенерировать и анализировать данные о BER. Функция MATLAB моделирует систему связи, производительность которой вы хотите изучить. BERTool вызывает симуляцию для значений _Eb/N0, которые вы задаете, собирает данные о BER от симуляции и создает график. BERTool также позволяет вам легко изменить область значений _Eb/N0 и критерий остановки для симуляции.

Чтобы изучить, как сделать ваши собственные функции симуляции совместимыми с BERTool, смотрите Функции Симуляции Использования с BERTool.

Пример: Используя Симуляцию MATLAB с BERTool. Этот пример иллюстрирует, как BERTool может запустить функцию симуляции MATLAB. Функцией является viterbisim, один из демонстрационных файлов, включенных с программным обеспечением Communications Toolbox.

Чтобы запустить этот пример, выполните эти шаги:

Откройте BERTool и перейдите к вкладке Monte Carlo. (Параметры по умолчанию зависят от того, установили ли вам программное обеспечение Communications Toolbox. Также обратите внимание, что поле BER variable name применяется только к моделям Simulink.)
Установите параметры как показано в следующей фигуре.
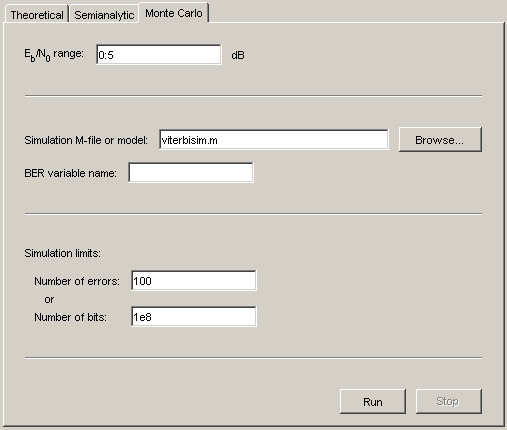
Нажмите Run.
BERTool запускает функцию симуляции однажды для каждого заданного значения _Eb/N0 и собирает данные о BER. (В то время как BERTool занят этой задачей, он не может обработать определенные другие задачи, включая отображение на графике данных из других вкладок графический интерфейса пользователя.)
Затем BERTool создает листинг в средстве просмотра данных.
BERTool отображает данные на графике в Окне рисунка BER.
Чтобы изменить область значений _Eb/N0 при сокращении количества битов, обработанных в каждом случае, введите [5 5.2 5.3] в поле Eb/No range, введите 1e5 в поле Number of bits и нажмите Run.
BERTool запускает функцию симуляции снова для каждого нового значения _Eb/N0 и собирает новые данные о BER. Затем BERTool создает другой листинг в средстве просмотра данных.
BERTool отображает данные на графике в Окне рисунка BER, настраивая горизонтальную ось, чтобы хранить новые данные.
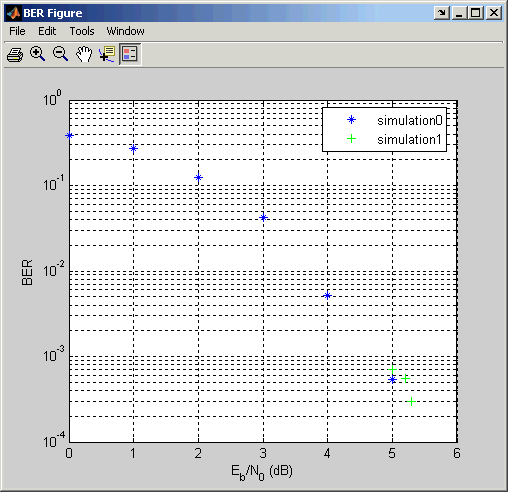
Две точки, соответствующие 5 дБ от этих двух наборов данных, отличаются, потому что меньшее значение Number of bits во второй симуляции заставило симуляцию заканчиваться прежде, чем наблюдать много ошибок. Чтобы узнать больше о критериях что использование BERTool для конечных симуляций, смотрите Варьирование Критерия остановки.

Для другого примера, который использует BERTool, чтобы запустить функцию симуляции MATLAB, смотрите Пример: Подготовьте Функцию Симуляции к Использованию с BERTool.

Отличаясь Критерий остановки. Когда вы создаете функцию симуляции MATLAB для использования с BERTool, необходимо управлять потоком так, чтобы симуляция закончилась, когда это или обнаруживает целевое количество ошибок или обрабатывает максимальное количество битов, какой бы ни происходит сначала. Чтобы узнать больше об этом требовании, смотрите Требования для Функций; для примера смотрите Пример: Подготовьте Функцию Симуляции к Использованию с BERTool.

После создания вашей функции, определенной целевой номер ошибок и максимальное количество битов во вкладке Monte Carlo BERTool.

Как правило, значение Number of errors, по крайней мере, 100 производит точный коэффициент ошибок. Значение Number of bits препятствует тому, чтобы симуляция запускалась слишком долго, особенно в больших значениях _Eb/N0. Однако, если значение Number of bits является столь маленьким, что симуляция собирает очень немного ошибок, коэффициент ошибок не может быть точным. Можно использовать доверительные интервалы, чтобы измерить точность коэффициентов ошибок, которые производит симуляция; чем больше доверительный интервал, тем менее точный вычисленный коэффициент ошибок.

Как пример, выполните процедуру, описанную в Примере: Используя Симуляцию MATLAB с BERTool и набором Confidence Level к 95 для каждого из этих двух наборов данных. Доверительные интервалы для второго набора данных больше, чем те для набора First Data. Это вызвано тем, что второй набор данных использует маленькое значение для Number of bits относительно свойств системы связи и значения в Eb/No range, приводящем к значениям BER только на основе небольшого количества наблюдаемых ошибок.

Примечание

Можно также использовать кнопку Stop в BERTool, чтобы остановить ряд симуляций преждевременно, пока функция настраивается, чтобы обнаружить и реагировать на нажатие кнопки.

Графический вывод Доверительных интервалов. После того, как вы запустите симуляцию с BERTool, получившийся набор данных в средстве просмотра данных имеет активное меню в столбце Confidence Level. Значением по умолчанию является off, так, чтобы данные моделирования в Окне рисунка BER не показывали доверительные интервалы.

Чтобы показать доверительные интервалы в Окне рисунка BER, установите Confidence Level на численное значение: 90%, 95% или 99%.

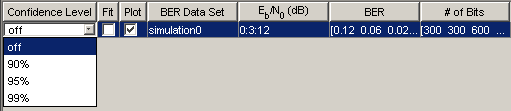
График в Окне рисунка BER сразу отвечает на ваш выбор. Демонстрационный график ниже.

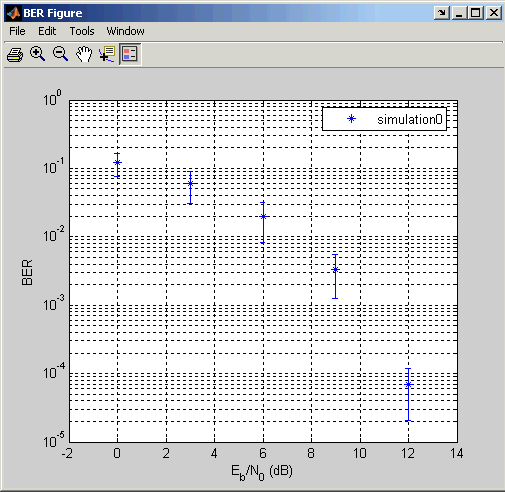
Для примера, который строит доверительные интервалы для симуляции Simulink, смотрите Пример: Используя Модель Simulink с BERTool.

Чтобы найти доверительные интервалы для уровней не перечисленными в меню Confidence Level, используйте функцию berconfint.

Подходящие Точки BER к Кривой. После того, как вы запустите симуляцию с BERTool, Окно рисунка BER строит отдельные точки данных BER. Чтобы соответствовать кривой к набору данных, который содержит по крайней мере четыре точки, выберите поле в столбце Fit средства просмотра данных.

График в Окне рисунка BER сразу отвечает на ваш выбор. Демонстрационный график ниже.

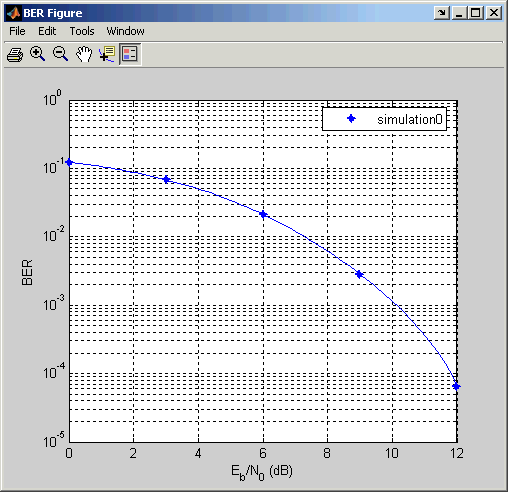
Для примера, который выполняет аппроксимирование кривыми для данных из симуляции Simulink и генерирует график, показанный выше, смотрите Пример: Используя Модель Simulink с BERTool. Для примера, который выполняет аппроксимирование кривыми для данных из функции симуляции MATLAB, смотрите Пример: Подготовьте Функцию Симуляции к Использованию с BERTool.

Для большей гибкости в процессе подбора кривой кривой к данным о BER используйте функцию berfit.

Используйте функции симуляции с BERTool

Требования для функций
Обработайте по шаблону для функции симуляции
Пример: подготовьте функцию симуляции к использованию с BERTool

Требования для Функций. Когда вы создаете функцию MATLAB для использования с BERTool, гарантируете, что функция взаимодействует правильно с графический интерфейсом пользователя. В этом разделе описываются входные параметры, выходные параметры и основную операцию BERTool-совместимой функции.

Входные параметры

BERTool оценивает ваши записи в областях графический интерфейса пользователя и передает данные функции как эти входные параметры в последовательности:

Одно значение от вектора Eb/No range каждый раз BERTool вызывает функцию симуляции
Значение Number of errors
Значение Number of bits

Выходные аргументы

Ваша функция симуляции должна вычислить и возвратить эти выходные аргументы в последовательности:

Частота ошибок по битам симуляции
Количество битов, обработанных при вычислении BER

BERTool использует эти выходные аргументы при создании отчетов и графическом выводе результатов.

Операция симуляции

Ваша функция симуляции должна выполнить эти задачи:

Моделируйте систему связи для значения _Eb/N0, заданного в первом входном параметре.
Прекратите моделировать, когда количество ошибок или количество обработанных битов будут равняться или будут превышать соответствующий порог, заданный во втором или третьем входном параметре, соответственно.
Обнаружьте, нажимаете ли вы Stop in BERTool и прерываете симуляцию в этом случае.

Обработайте по шаблону для Функции Симуляции. Используйте следующий шаблон при адаптации кода, чтобы работать с BERTool. Можно открыть его в редакторе путем ввода edit bertooltemplate в Окно Команды MATLAB. Понимание Шаблона объясняет ключевые разделы шаблона, в то время как Используя Шаблон указывает, как использовать шаблон с вашим собственным кодом симуляции. Также можно разработать функцию симуляции, не используя шаблон, но быть уверены, что это удовлетворяет требования, описанные в Требованиях для Функций.

Примечание

Шаблон еще не готов к употреблению с BERTool. Необходимо ввести собственный код симуляции в местах, отмеченных INSERT YOUR CODE HERE. Для полного примера на основе этого шаблона смотрите Пример: Подготовьте Функцию Симуляции к Использованию с BERTool.

function [ber, numBits] = bertooltemplate(EbNo, maxNumErrs, maxNumBits)
% Import Java class for BERTool.
import com.mathworks.toolbox.comm.BERTool;

% Initialize variables related to exit criteria.
berVec = zeros(3,1); % Updated BER values

% --- Set up parameters. ---
% --- INSERT YOUR CODE HERE.
% Simulate until number of errors exceeds maxNumErrs
% or number of bits processed exceeds maxNumBits.
while((berVec(2) < maxNumErrs) && (berVec(3) < maxNumBits))

   % Check if the user clicked the Stop button of BERTool.
   if (BERTool.getSimulationStop)
      break;
   end

   % --- Proceed with simulation.
   % --- Be sure to update totErr and numBits.
   % --- INSERT YOUR CODE HERE.
end % End of loop

% Assign values to the output variables.
ber = berVec(1);
numBits = berVec(3);

Понимание шаблона.

От изучения кода в шаблоне функции наблюдайте, как функция или удовлетворяет требования, перечисленные в Требованиях для Функций, или указывает, где ваши собственные вставки кода должны сделать так. В частности,

Функция имеет соответствующие аргументы ввода и вывода.
Функция включает заполнителя для кода, который моделирует систему для данного значения E_b/N0.
Функция использует циклическую структуру, чтобы прекратить моделировать, когда количество ошибок превышает maxNumErrs, или количество битов превышает maxNumBits, какой бы ни происходит сначала.
Примечание
Несмотря на то, что оператор while цикла описывает выходные критерии, ваш собственный код, введенный в раздел, отмеченный, Proceed with simulation должен вычислить количество ошибок и количество битов. Если вы не выполняете эти вычисления в своем собственном коде, нажатие по Stop является единственным способом отключить цикл.
В каждой итерации цикла функция обнаруживает, когда пользователь нажимает Stop in BERTool.

Используя шаблон.

Вот процедура для использования шаблона с вашим собственным кодом симуляции:

Определите задачи настройки, которые необходимо выполнить. Например, вы можете хотеть инициализировать переменные, содержащие размер алфавита модуляции, коэффициенты фильтра, сверточную решетку кодирования или состояния сверточного interleaver. Поместите код для этих задач настройки в разделе шаблона отметил Set up parameters.
Определите базовые задачи симуляции, приняв, что вся настройка работает, был уже выполнен. Например, эти задачи могут включать кодирование контроля ошибок, модуляцию/демодуляцию и моделирование канала. Поместите код для этих базовых задач симуляции в разделе шаблона отметил Proceed with simulation.
Также в разделе шаблона, отмеченном Proceed with simulation, включайте код, который обновляет значения totErr и numBits. Количество totErr представляет количество ошибок, наблюдаемых до сих пор. Количество numBits представляет количество битов, обработанных до сих пор. Вычисления, чтобы обновить эти переменные зависят от того, как работают ваши базовые задачи симуляции.
Примечание
Обновление количеств ошибок и битов важно для обеспечения, что цикл останавливается. Однако, если вы случайно создаете бесконечный цикл рано в вашей технической разработке с помощью шаблона функции, нажмите Stop in BERTool, чтобы прервать симуляцию.
Не используйте любой код настройки, который инициализирует EbNo, maxNumErrs или maxNumBits, потому что BERTool передает эти количества функции как входные параметры после оценки данных, вводимых в графический интерфейс пользователя.
Настройте свой код или код шаблона по мере необходимости, чтобы использовать сопоставимые имена переменных и значения. Например, если ваш оригинальный код использует переменную под названием ebn0, и объявление функции шаблона (первая строка) использует имя переменной EbNo, необходимо поменять одно из имен, таким образом, они соответствуют. Как другой пример, если ваш оригинальный код использует ОСШ вместо E_b/N0, необходимо преобразовать количества соответственно.

Пример: Подготовьте Функцию Симуляции к Использованию с BERTool. Этот раздел адаптирует шаблон функции, данный в Шаблоне для Функции Симуляции.

Подготовка функции

Чтобы подготовить функцию к использованию с BERTool, выполните эти шаги:

Скопируйте шаблон с Шаблона для Функции Симуляции в новый файл MATLAB в редакторе MATLAB. Сохраните его в папке на своем пути MATLAB с помощью имени файла bertool_simfcn.
От исходного примера следующие строки являются задачами настройки. Они изменяются от исходного примера, чтобы полагаться на входные параметры, которые BERTool предоставляет функции, вместо того, чтобы задать переменные, такие как EbNovec и numerrmin непосредственно.
```
% Set up initial parameters.
siglen = 1000; % Number of bits in each trial
M = 2; % DBPSK is binary.
% DBPSK modulation and demodulation System objects
hMod  = comm.DBPSKModulator;
hDemod = comm.DBPSKDemodulator;
% AWGNChannel System object
hChan = comm.AWGNChannel('NoiseMethod', 'Signal to noise ratio (SNR)');
% ErrorRate calculator System object to compare decoded symbols to the
% original transmitted symbols.
hErrorCalc = comm.ErrorRate;
snr = EbNo; % Because of binary modulation
hChan.SNR = snr; %Assign Channel SNR
```
Поместите эти строки кода в разделе шаблона отметили Set up parameters.

От исходного примера следующие строки являются базовыми задачами симуляции, после того, как вся настройка работает, был выполнен.

msg = randi([0,M-1], siglen, 1); % Generate message sequence.
txsig = step(hMod, msg); % Modulate.
hChan.SignalPower = (txsig'*txsig)/length(txsig);  % Calculate and
                                                % assign signal power
rxsig = step(hChan,txsig); % Add noise.
decodmsg = step(hDemod, rxsig); % Demodulate.
berVec = step(hErrorCalc, msg, decodmsg); % Calculate BER

Поместите код для этих базовых задач симуляции в разделе шаблона отметил Proceed with simulation.

Функция bertool_simfcn теперь совместима с BERTool. Обратите внимание на то, что различающийся исходный пример, функция здесь не инициализирует EbNovec, задает EbNo как скаляр или использует numerrmin в качестве целевого количества ошибок; это вызвано тем, что BERTool обеспечивает входные параметры для подобных количеств. Функция bertool_simfcn также исключает код, связанный с графическим выводом, аппроксимированием кривыми и доверительными интервалами в исходном примере, потому что BERTool позволяет вам сделать подобные задачи в интерактивном режиме без написания кода.

Используя подготовленную функцию

Чтобы использовать bertool_simfcn в сочетании с BERTool, продолжите пример путем выполнения этих шагов:

Откройте BERTool и перейдите к вкладке Monte Carlo.
Установите параметры на вкладке Monte Carlo как показано в следующей фигуре.
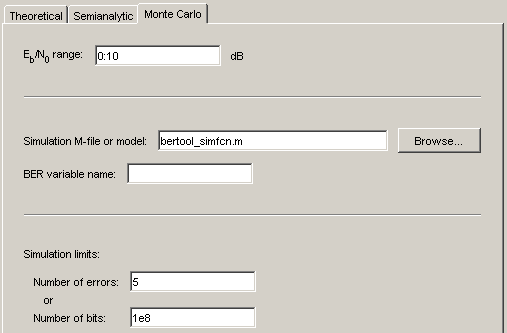
Нажмите Run.
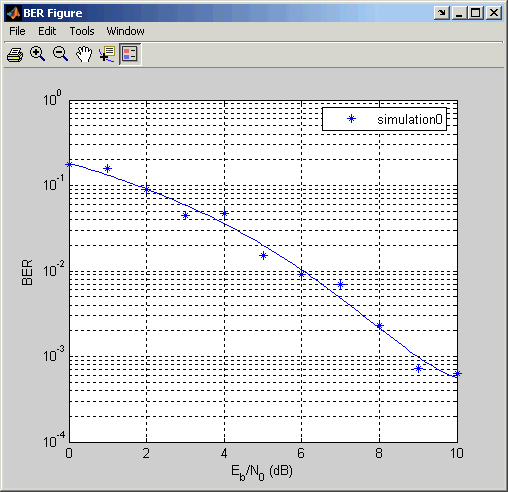
BERTool тратит результаты вычисления некоторого времени и затем строит их. Они, кажется, не падают вдоль плавной кривой, потому что симуляция потребовала только пяти ошибок для каждого значения в EbNo.
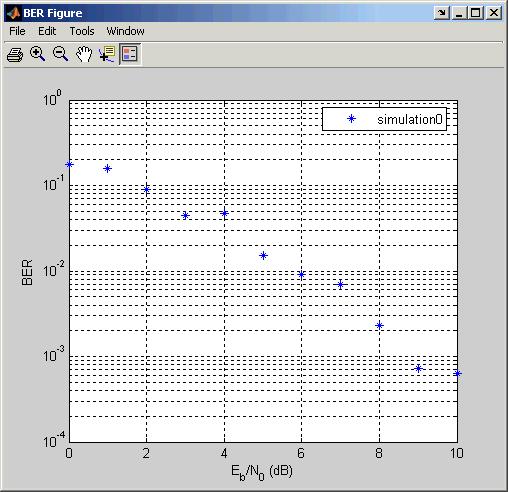
Чтобы соответствовать кривой к серии точек в Окне рисунка BER, выберите поле рядом с Fit в средстве просмотра данных.
BERTool строит кривую, как показано в следующей фигуре.

Запустите симуляции Simulink

Разделите обзор
Пример: Используя модель Simulink с BERTool
Отличаясь критерий остановки

Разделите Обзор. Можно использовать BERTool в сочетании с моделями Simulink, чтобы сгенерировать и анализировать данные о BER. Модель Simulink моделирует систему связи, производительность которой вы хотите изучить, в то время как BERTool управляет рядом симуляций с помощью модели и собирает данные о BER.

Примечание

Чтобы использовать модели Simulink в BERTool, у вас должна быть лицензия Simulink. Программное обеспечение Communications Toolbox настоятельно рекомендовано. Остальная часть этого раздела принимает, что у вас есть лицензия и на Simulink и на приложения Communications Toolbox.

Чтобы получить доступ к возможностям BERTool, связанного с моделями Simulink, откройте вкладку Monte Carlo.

Для получения дальнейшей информации о доверительных интервалах и аппроксимировании кривыми для данных моделирования, смотрите Доверительные интервалы Графического вывода и Подходящие Точки BER к Кривой, соответственно.

Пример: Используя Модель Simulink с BERTool. Этот пример иллюстрирует, как BERTool может управлять рядом симуляций модели Simulink, и как можно отличаться график. Моделью является commgraycode, одна из демонстрационных моделей, включенных с программным обеспечением Communications Toolbox. Пример принимает, что вам установили программное обеспечение Communications Toolbox.

Чтобы запустить этот пример, выполните эти шаги:

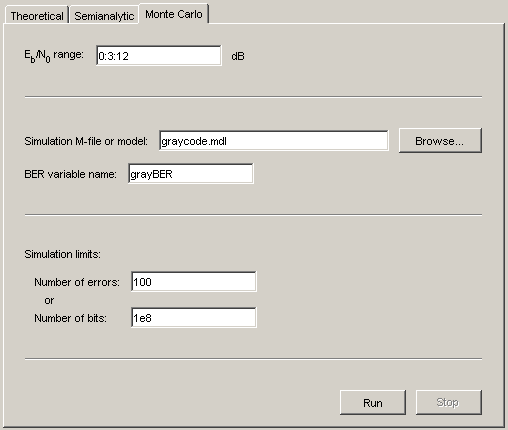
Откройте BERTool и перейдите к вкладке Monte Carlo. Имя файла модели, commgraycode.mdl, появляется как параметр Simulation MATLAB file or Simulink model. (Если viterbisim.m появляется там, выберите, чтобы указать, что программное обеспечение Communications Toolbox установлено.)
Нажмите Run.
BERTool загружает модель в память (который в свою очередь инициализирует несколько переменных в рабочем пространстве MATLAB), запускает симуляцию однажды для каждого значения _Eb/N0 и собирает данные о BER. BERTool создает листинг в средстве просмотра данных.
BERTool отображает данные на графике в Окне рисунка BER.
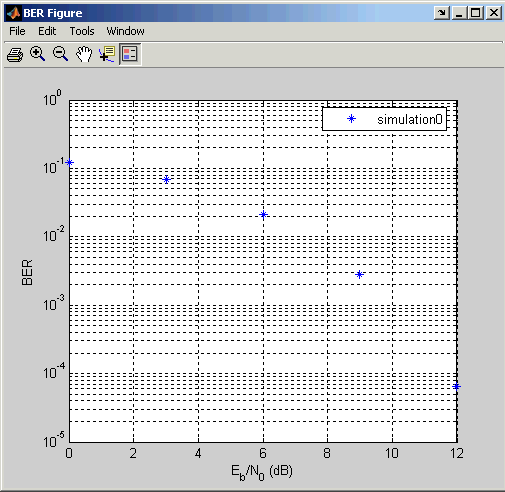
Чтобы соответствовать кривой к серии точек в Окне рисунка BER, выберите поле рядом с Fit в средстве просмотра данных.
BERTool строит кривую, как ниже.
Чтобы указать на 99%-й доверительный интервал вокруг каждой точки в данных моделирования, установите Confidence Level на 99% в средстве просмотра данных.
BERTool отображает значение погрешности, чтобы представлять доверительные интервалы, как ниже.

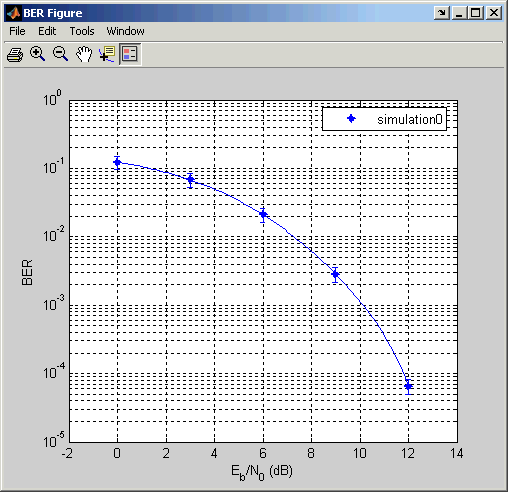
Другой пример, который использует BERTool, чтобы управлять рядом симуляций Simulink, находится в Примере: Подготовьте Модель к Использованию с BERTool.

Отличаясь Критерий остановки. Когда вы создаете модель Simulink для использования с BERTool, необходимо настроить его так, чтобы симуляция закончилась, когда это или обнаруживает целевое количество ошибок или обрабатывает максимальное количество битов, какой бы ни происходит сначала. Чтобы узнать больше об этом требовании, смотрите Требования для Моделей; для примера смотрите Пример: Подготовьте Модель к Использованию с BERTool.

После создания вашей модели Simulink, определенной целевой номер ошибок и максимальное количество битов во вкладке Monte Carlo BERTool.

Можно также нажать Stop in BERTool, чтобы остановить ряд симуляций преждевременно.

Используйте модели Simulink с BERTool

Требования для моделей
Советы для подготовки моделей
Пример: подготовьте модель к использованию с BERTool

Требования для Моделей. Модель Simulink должна удовлетворить эти требования, прежде чем можно будет использовать ее с BERTool, где чувствительные к регистру имена переменных должны быть точно как показано ниже:

Блок канала должен использовать переменную EbNo, а не трудно закодированное значение для _Eb/N0.
Симуляция должна остановиться, когда ошибочное количество достигает значения переменной maxNumErrs или когда количество обработанных битов достигает значения переменной maxNumBits, какой бы ни происходит сначала.
Можно сконфигурировать блок Error Rate Calculation в программном обеспечении Communications Toolbox, чтобы остановить симуляцию на основе таких критериев.
Симуляция должна отправить данные об уровне конечной погрешности в рабочее пространство MATLAB как переменная, имя которой вы вводите в поле BER variable name в BERTool. Переменная должна быть трехэлементным вектором, который перечисляет BER, количество битовых ошибок и количество обработанных битов.
Этот трехэлементный векторный формат поддерживается блоком Error Rate Calculation.

Советы для Подготовки Моделей. Вот некоторые советы для подготовки модели Simulink для использования с BERTool:

Чтобы избегать использования имени неопределенной переменной в диалоговом окне для блока Simulink на шагах, которые следуют, настройте переменные в рабочем пространстве MATLAB с помощью команды, такие как та ниже.
```
EbNo = 0; maxNumErrs = 100; maxNumBits = 1e8;
```
Вы можете также хотеть поместить ту же команду в коллбэк функции предварительной нагрузки модели, инициализировать переменные, если вы вновь открыли модель в будущем сеансе работы с MATLAB.
Когда вы используете BERTool, он обеспечивает фактические значения на основе того, что вы вводите в графический интерфейс пользователя, таким образом, начальные значения выше несколько произвольны.
Чтобы смоделировать канал, используйте блок AWGN Channel в программном обеспечении Communications Toolbox с этими параметрами:
- Mode = Signal to noise ratio (Eb/No)
- Eb/No = EbNo
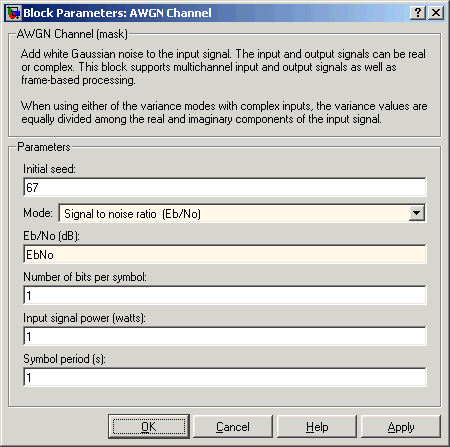
Чтобы вычислить коэффициент ошибок, используйте блок Error Rate Calculation в программном обеспечении Communications Toolbox с этими параметрами:
- Проверяйте Stop simulation.
- Target number of errors = maxNumErrs
- Maximum number of symbols = maxNumBits
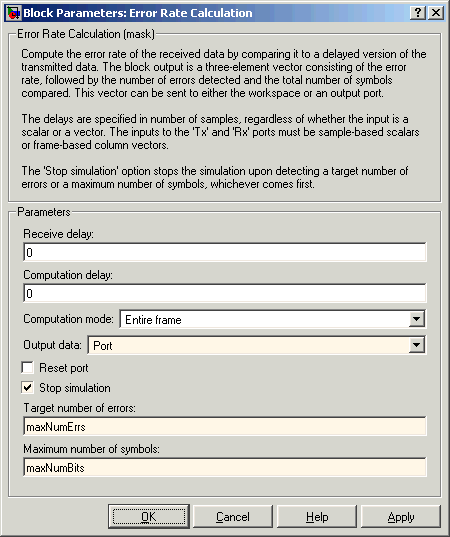
Чтобы отправить данные от блока Error Rate Calculation до рабочего пространства MATLAB, установите Output data на Port, присоедините блок To Workspace и установите параметр Limit data points to last последнего блока на 1. Параметр Variable name в блоке To Workspace должен совпадать со значением, которое вы вводите в поле BER variable name BERTool.
Совет
Больше чем один блок To Workspace доступен. Обязательно выберите To Workspace из подбиблиотеки DSP System Toolbox™ / Sinks.
Если ваша модель вычисляет коэффициент ошибок символа вместо небольшого коэффициента ошибок, используйте блок Integer to Bit Converter в программном обеспечении Communications Toolbox, чтобы преобразовать символы вдребезги.
Обрабатываются основанные на кадре симуляции, часто запускаемые быстрее, чем основанные на выборке симуляции для того же количества битов. Количество ошибок или количество обработанных битов могут превысить значения, которые вы вводите в BERTool, потому что симуляция всегда обрабатывает установленную сумму данных в каждом кадре.
Если у вас есть существующая модель, которая использует блок AWGN Channel с помощью параметра Mode кроме Signal to noise ratio (Eb/No), можно адаптировать блок, чтобы использовать режим Eb/No вместо этого. Чтобы узнать о том, как различные режимы блока связаны друг с другом, нажмите кнопку Help блока AWGN Channel, чтобы просмотреть онлайновую страницу с описанием.
Если ваша модель использует функцию предварительной нагрузки или другой коллбэк, чтобы инициализировать переменные в рабочем пространстве MATLAB после загрузки, убедитесь, прежде чем вы будете использовать кнопку Run в BERTool, что одно из этих условий соблюдают:
- Модель не находится в настоящее время в памяти. В этом случае BERTool загружает модель в память и запускает функции обратного вызова.
- Модель находится в памяти (ли в окне или не), и переменные неповреждены.
Если вы очищаете или перезаписываете переменные модели и хотите восстановить их значения перед использованием кнопки Run в BERTool, можно использовать функцию bdclose в Окне Команды MATLAB, чтобы очистить модель из памяти. Это заставляет BERTool перезагружать модель после того, как вы нажмете Run. Точно так же, если вы обновляете свою рабочую область путем издания clear all или команды clear variables, необходимо также очистить модель из памяти при помощи bdclose all.

Пример: Подготовьте Модель к Использованию с BERTool. Этот пример использует модель Simulink, которая настраивается для использования с BERTool. Пример также иллюстрирует, как сравнить производительность BER симуляции Simulink с теоретическими результатами BER. Пример принимает, что вам установили программное обеспечение Communications Toolbox.

Чтобы подготовить модель к использованию с BERTool, выполните эти шаги, с помощью точных чувствительных к регистру имен переменных как показано:

Откройте модель путем ввода следующей команды в Окно Команды MATLAB.
```
doc_bpsk
```
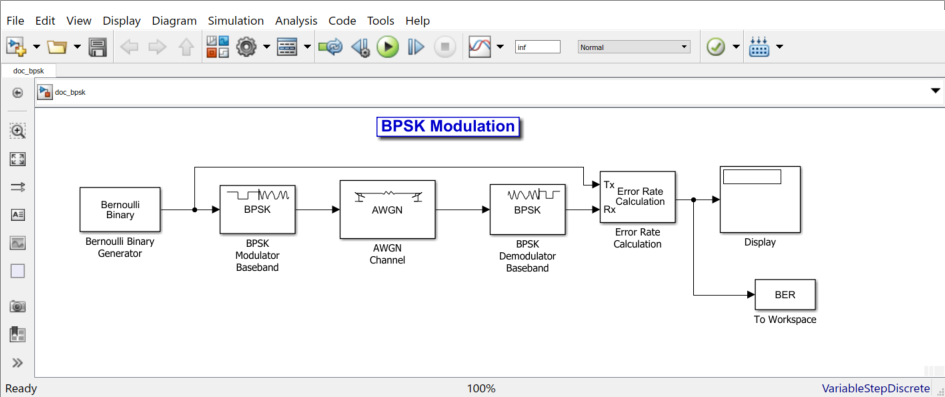
Чтобы инициализировать параметры в рабочем пространстве MATLAB и избегать использования неопределенных переменных как параметров блоков, введите следующую команду в Окно Команды MATLAB.
```
EbNo = 0; maxNumErrs = 100; maxNumBits = 1e8;
```
Чтобы гарантировать, что BERTool использует правильное количество шума каждый раз, это запускает симуляцию, откройте диалоговое окно для блока AWGN Channel путем двойного клика по блоку. Проверьте, что Es/No установлен в EbNo, и нажмите OK. В этой конкретной модели _Es/N0 эквивалентен _Eb/N0, потому что тип модуляции является BPSK.
Гарантировать, что BERTool использует правильный критерий остановки для каждой итерации,
- Откройте диалоговое окно для блока Error Rate Calculation. Проверьте, что Target number of errors установлен в maxNumErrs, и что Maximum number of symbols установлен в maxNumBits. Нажмите OK.
- Время остановки симуляции должно быть установлено в Inf.
Чтобы позволить BERTool получить доступ к результатам BER, которые вычисляет блок Error Rate Calculation, блок To Workspace, BER, соединяется с выводом блока Error Rate Calculation.
Совет
Больше чем один блок To Workspace доступен. Обязательно выберите To Workspace из подбиблиотеки DSP System Toolbox / Sinks.

Чтобы использовать модель doc_bpsk с BERTool, выполните эти шаги:

Откройте BERTool и перейдите к вкладке Monte Carlo.
Установите параметры на вкладке Monte Carlo как показано в следующей фигуре.
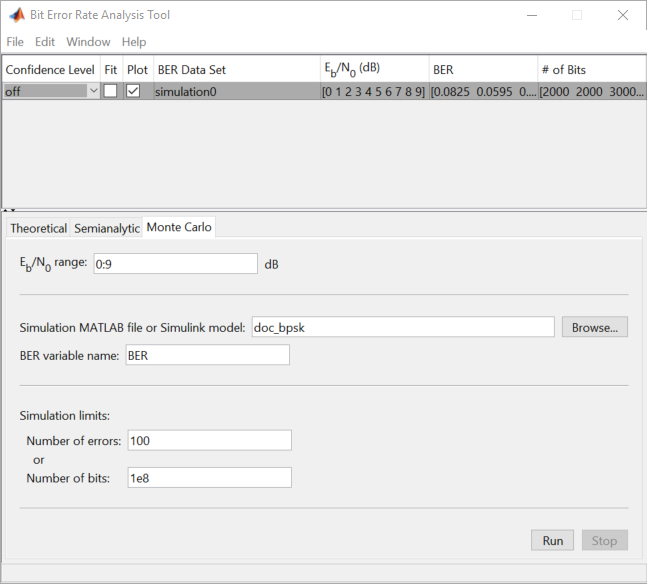
Нажмите Run.
BERTool тратит результаты вычисления некоторого времени и затем строит их.
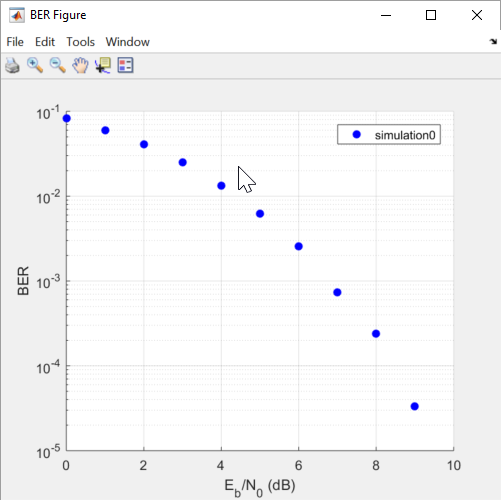
Чтобы сравнить эти результаты симуляции с теоретическими результатами, перейдите к вкладке Theoretical в BERTool и установите параметры как показано ниже.
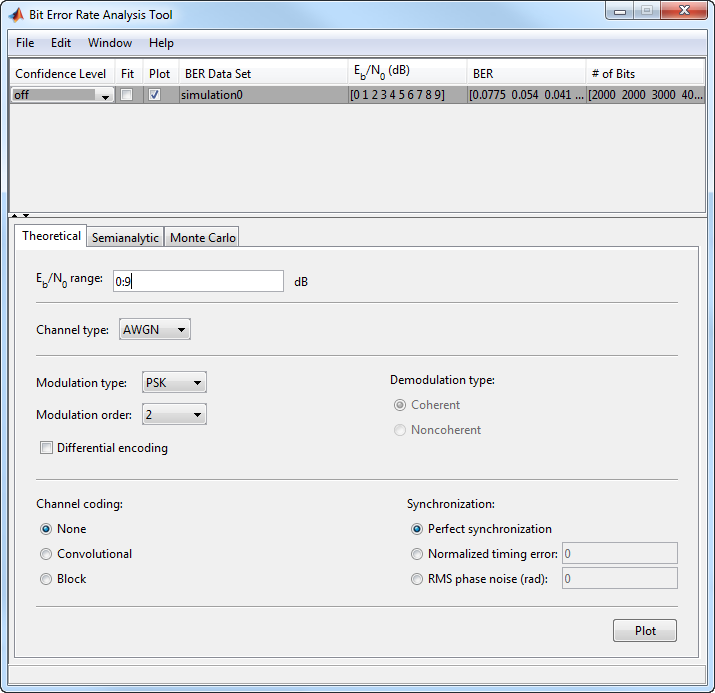
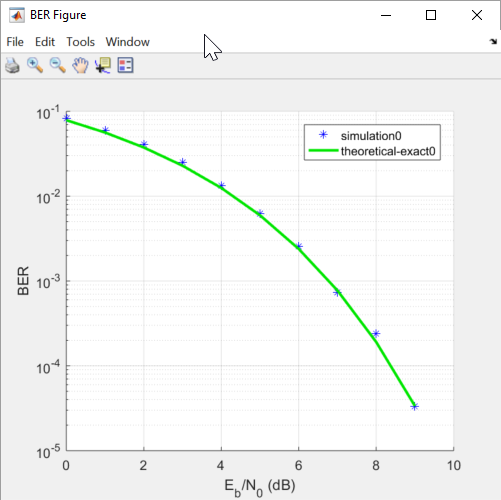
Нажмите Plot.
BERTool строит теоретическую кривую в Окне рисунка BER наряду с более ранними результатами симуляции.

Управляйте данными о BER

Экспорт наборов данных или сеансов BERTool
Импорт наборов данных или сеансов BERTool
Данные об управлении в средстве просмотра данных

Экспорт Наборов данных или Сеансов BERTool. BERTool позволяет вам экспортировать отдельные наборы данных в рабочее пространство MATLAB или в MAT-файлы. Одна опция для экспорта удобна для обработки данных вне BERTool. Например, чтобы создать очень индивидуально настраиваемый отображают данные об использовании на графике из BERTool, экспортируют набор данных BERTool в рабочее пространство MATLAB и используют любую из команд графического вывода в MATLAB. Другая опция для экспорта позволяет вам повторно импортировать данные в BERTool позже.

BERTool также позволяет вам сохранить целый сеанс, который полезен, если ваш сеанс содержит несколько наборов данных, к которым вы хотите возвратиться на более позднем сеансе.

В этом разделе описываются эти возможности:

Экспорт наборов данных

Чтобы экспортировать отдельный набор данных, выполните эти шаги:

В средстве просмотра данных выберите набор данных, который вы хотите экспортировать.
Выберите File > Export Data.
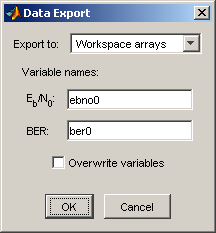
Установите Export to указывать на формат и место назначения данных.
1. Если вы хотите повторно импортировать данные в BERTool позже, необходимо выбрать Workspace structure или MAT-file structure, чтобы создать структуру в рабочем пространстве MATLAB или MAT-файле, соответственно.
  Появляется новое поле под названием Structure name. Установите его на имя, которое вы хотите, чтобы BERTool использовал для структуры, которую это создает.
  Если вы выбрали Workspace structure, и вы хотите, чтобы BERTool использовал ваше выбранное имя переменной, даже если переменная тем именем уже существует в рабочей области, выберите Overwrite variables.
2. Если вы не должны повторно импортировать данные в BERTool позже, удобный способ получить доступ к данным вне BERTool состоит в том, чтобы иметь BERTool, создают пару массивов в рабочем пространстве MATLAB. Один массив содержит значения _Eb/N0, в то время как другой массив содержит значения BER. Чтобы выбрать эту опцию, установите Export to на Workspace arrays.
  Затем введите два имен переменных в полях под Variable names.
  Если вы хотите, чтобы BERTool использовал ваши выбранные имена переменных, даже если переменные теми именами уже существуют в рабочей области, выберите Overwrite variables.
Нажмите OK. Если вы выбрали MAT-file structure, BERTool предлагает вам путь к MAT-файлу, который вы хотите создать.

Чтобы повторно импортировать структуру позже, смотрите Наборы данных Импорта.

Исследование экспортируемой структуры

Этот раздел кратко описывает содержимое структуры, которую BERTool экспортирует в рабочую область или в MAT-файл. Поля структуры обозначаются в приведенной ниже таблице. Полями, которые являются самыми важными для вас когда это необходимо, чтобы управлять экспортированными данными, является paramsEvaled и data.

Имя поля	Значение
`params`	Значения параметров в БЕРТОЛЕ ГИ, некоторые из которых могут быть невидимыми и следовательно не важными для вычислений.
`paramsEvaled`	Значения параметров, которые BERTool использует при вычислении набора данных.
`data`	_Eb/N0, BER и количество битов обрабатываются.
`dataView`	Информация о внешнем виде в средстве просмотра данных. Используемый BERTool для переимпорта данных.
`cellEditabilities`	Указывает, имеет ли средство просмотра данных активный Confidence Level или запись Fit. Используемый BERTool для переимпорта данных.

Поля параметра

Поля params и paramsEvaled подобны друг другу, за исключением того, что params описывает точное состояние графический интерфейса пользователя, тогда как paramsEvaled указывает на значения, которые на самом деле используются для вычислений. Когда пример различия, для теоретической системы с каналом AWGN, записями params, но paramsEvaled не использует параметр порядка разнообразия. Порядок разнообразия не используется в вычислениях, потому что это важно только для систем с каналами Рейли. Как другой пример, если вы вводите [0:3]+1 в графический интерфейсе пользователя как область значений значений _Eb/N0, params указывает на [0:3]+1, в то время как paramsEvaled указывает на 1 2 3 4.

Длина и точное содержимое paramsEvaled зависят от набора данных, потому что только релевантная информация появляется. Если значение содержимого paramsEvaled не ясно после контроля, один способ узнать больше состоит в том, чтобы повторно импортировать набор данных в BERTool и осмотреть значения параметров, которые появляются в графический интерфейсе пользователя. Чтобы повторно импортировать структуру, следуйте инструкциям в Импорте Наборов данных или Сеансов BERTool.

Поле данных

Если ваша экспортируемая переменная рабочей области называется ber0, поле ber0.data является массивом ячеек, который содержит числовые результаты в этих векторах:

ber0.data{1} перечисляет значения _Eb/N0.
ber0.data{2} перечисляет значения BER, соответствующие каждому из значений _Eb/N0.
ber0.data{3} указывает для симуляции или полуаналитических результатов, сколько битов BERTool обработал при вычислении каждого из соответствующих значений BER.

Сохранение сеанса BERTool.

Чтобы сохранить целый сеанс BERTool, выполните эти шаги:

Выберите File > Save Session.
Когда BERTool предлагает вам, введите путь к файлу, который вы хотите создать.

BERTool создает текстовый файл, который записывает все наборы данных в настоящее время в средстве просмотра данных, наряду с параметрами графический интерфейса пользователя, сопоставленными с наборами данных.

Примечание

Если ваш сеанс BERTool требует конкретных переменных рабочей области (таких как txsig или rxsig для вкладки Semianalytic), сохраните тех отдельно в MAT-файле с помощью команды save в MATLAB.

Импорт Наборов данных или Сеансов BERTool. BERTool позволяет вам повторно импортировать отдельные наборы данных, которые вы ранее экспортировали в структуру, или перезагружать целые сеансы что вы ранее сохраненный. В этом разделе описываются эти возможности:

Чтобы узнать больше об экспорте наборов данных или сохранении сеансов от BERTool, смотрите Наборы данных Экспорта или Сеансы BERTool.

Импорт наборов данных.

Чтобы импортировать отдельный набор данных, который вы ранее экспортировали от BERTool до структуры, выполните эти шаги:

Выберите File > Import Data.
Установите Import from или на Workspace structure или на MAT-file structure. Если вы выбираете Workspace structure, вводите имя переменной рабочей области в поле Structure name.
Нажмите OK. Если вы выбираете MAT-file, BERTool предлагает вам выбирать файл, который содержит структуру, которую вы хотите импортировать.

После того, как вы отклоняете диалоговое окно Data Import (и диалоговое окно выбора файла, в случае MAT-файла), средство просмотра данных показывает недавно импортированный набор данных, и Окно рисунка BER строит его.

Открытие предыдущего сеанса BERTool

Чтобы заменить наборы данных в средстве просмотра данных с наборами данных от предыдущего сеанса BERTool, выполните эти шаги:

Выберите File > Open Session.
Примечание
Если BERTool уже содержит наборы данных, он спрашивает вас, хотите ли вы сохранить текущий сеанс. Если вы отвечаете не и продолжаете процесс загрузки, BERTool отбрасывает текущий сеанс после открытия нового сеанса из файла.
Когда BERTool предлагает вам, введите путь к файлу, который вы хотите открыть. Это должен быть файл, что вы ранее создали использование опции Save Session в BERTool.

После того, как BERTool читает файл сеанса, средство просмотра данных показывает наборы данных из файла.

Если ваш сеанс BERTool требует конкретных переменных рабочей области (таких как txsig или rxsig для вкладки Semianalytic), что вы сохраненный отдельно в MAT-файле, можно получить их использующий команду load в MATLAB.

Данные об управлении в Средстве просмотра Данных. Средство просмотра данных дает вам гибкость, чтобы переименовать и удалить наборы данных и переупорядочить столбцы в средстве просмотра данных.

Чтобы переименовать набор данных в средстве просмотра данных, дважды кликните его имя в столбце BER Data Set и введите новое имя.
Чтобы удалить набор данных из средства просмотра данных, выберите его и выберите Edit > Delete.
Примечание
Если набор данных произошел из вкладки Semianalytic или Theoretical, BERTool удаляет данные, не прося подтверждение. Вы не можете отменить эту операцию.
Чтобы переместить столбец в средство просмотра данных, перетащите заголовок столбца налево или направо с мышью. Например, изображение ниже показов мышь, перетаскивающая столбец BER слева от его положения по умолчанию. Когда вы отпускаете кнопку мыши, столбцы привязываются в место.

Тестовая консоль коэффициента ошибок

Тестовая Консоль Коэффициента ошибок является объектом, способным к рабочим симуляциям для систем связи, чтобы измерить уровень коэффициента ошибок.

Тестовая Консоль Коэффициента ошибок совместима с системами связи, созданными с определенным API, заданным testconsole. Класс SystemBasicAPI. В рамках этого определения класса вы задаете функциональность системы связи.

Вы присоединяете систему к Тестовой Консоли Коэффициента ошибок, чтобы запустить симуляции и получить данные о коэффициенте ошибок.

Вы получаете результаты коэффициента ошибок в других местах в системе под тестом путем определения уникальных тестовых точек. Каждая тестовая точка содержит пару зондов, которые система использует для данных логов к тестовой консоли. Информация, которую вы указываете с тестовой консолью, задает, как каждая пара тестовых зондов сравнивает данные. Например, в основанной на кадре системе, Тестовая Консоль Коэффициента ошибок может сравнить переданные и полученные биты заголовка или переданные и полученные биты данных. Точно так же это может сравнить ошибочные количества CRC, чтобы получить коэффициенты ошибок кадра в различных точках в системе. Можно также сконфигурировать Тестовую Консоль Коэффициента ошибок, чтобы сравнить данные в нескольких парах зондов, получив несколько результатов коэффициента ошибок.

Можно запустить симуляции со столькими тестовыми параметрами, сколько желаемый, проанализируйте результаты и получите параметрические или объемные поверхностные диаграммы путем определения, какие параметры действуют как независимые переменные.

Существует две основных задачи, сопоставленные с использованием Тестовой Консоли Коэффициента ошибок: Создание Системы и Присоединение Системы к Тестовой Консоли Коэффициента ошибок.

Когда вы запускаете систему, которая не присоединена к Тестовой Консоли Коэффициента ошибок, система запускается в режиме отладки. Режим отладки полезен при оценке или отладке кода для системы, которую вы разрабатываете.

Чтобы видеть полномасштабный пример при создании системы и рабочих симуляций, смотрите Симуляции Частоты ошибок по битам Для Различных Стоимостей заказов Eb/No и Модуляции.

Следующие разделы описывают Тестовую Консоль Коэффициента ошибок и ее функциональность:

Создание системы
Методы, разрешающие вам связываться с тестовой консолью коэффициента ошибок во время выполнения симуляции
Режим отладки
Запустите симуляции Используя тестовую консоль коэффициента ошибок
Симуляции Частоты ошибок по битам Для Различных Стоимостей заказов Eb/No и Модуляции

Создание системы

Вы присоединяете систему к Тестовой Консоли Коэффициента ошибок, чтобы запустить симуляции и получить данные о коэффициенте ошибок. Когда вы присоединяете систему под тестом, вы также указываете определенную информацию к тестовой консоли в порядке задать тестовые воздействия системы, тестовые параметры и тестовые зонды.

При создании системы связи для использования с Тестовой Консолью Коэффициента ошибок, включает следующие шаги.

Запись системного класса, расширение testconsole. Класс SystemBasicAPI.
Запись регистрационного метода
- Регистрация является связанным тестом
- Задает элементы, такие как тестовые параметры, тестовые зонды и тестовые воздействия
Запись метода настройки
Запись метода сброса
Запись метода выполнения
Методы позволяют системе связываться с тестовой консолью.

Чтобы видеть системный файл, перейдите к следующему местоположению:

matlab\toolbox\comm\comm \+ commtest

Затем введите следующий синтаксис в командной строке MATLAB:

edit MPSKSYSTEM.m

Запись Метода Регистра. Используя метод register, вы указываете тестовые воздействия, тестируете параметры и тестируете зонды к Тестовой Консоли Коэффициента ошибок. Вы указываете эти элементы к Тестовой Консоли Коэффициента ошибок с помощью registerTestInput, registerTestParameter и методов registerTestProbe.

Запишите метод register для каждой системы связи, которую вы создаете.
Если вы не реализуете метод register для системы, можно все еще присоединить систему к Тестовой Консоли Коэффициента ошибок. В то время как тестовая консоль запускает конкретное количество итераций в системе, вы не можете управлять параметрами симуляции или получить результаты симуляции.

Регистрация тестовых воздействий

В порядке запустить симуляции, система под тестом запрашивает тестовые воздействия от Тестовой Консоли Коэффициента ошибок. Эти тестовые воздействия обеспечивают данные, ведущие симуляции для системы под тестом.

Система под тестом не может запросить определенный входной тип, пока вы не присоединяете его к Тестовой Консоли Коэффициента ошибок. Кроме того, определенный входной тип должен быть указан к тестовой консоли.

В методе register вы вызываете метод registerTestInput(sys,inputName), чтобы указать тестовые воздействия.

sys представляет указатель на пользовательский системный объект.
inputName представляет имя входа, который указывает система. Это имя должно совпасть с именем доступного тестового воздействия в Тестовой Консоли Коэффициента ошибок, или ошибка происходит.
- 'NumTransmissions' - вызов метода getInput возвращает длину кадра. Сама система ответственна за генерацию кадра данных с помощью источника данных.
- 'RandomIntegerSource' - вызов метода getInput возвращает вектор символов с длиной, которую задает свойство Error Rate Test Console FrameLength. Если система указывает этот исходный тип, то это должно также указать тестовый параметр под названием 'M', который соответствует порядку модуляции.

Регистрация тестовых параметров

Тестовые параметры являются системными параметрами, для которых Тестовая Консоль Коэффициента ошибок получает результаты симуляции. Вы задаете область значений развертки этих параметров с помощью Тестовой Консоли Коэффициента ошибок и получаете результаты симуляции для различных системных условий.

Система под тестом указывает системный параметр к Тестовой Консоли Коэффициента ошибок, создавая тестовый параметр. Вы указываете тестовый параметр к Тестовой Консоли Коэффициента ошибок с помощью метода registerTestParameter(sys,name,default,validRange).

sys представляет указатель на пользовательский системный объект
name представляет название параметра, которое система указывает к Тестовой Консоли Коэффициента ошибок
default задает значение по умолчанию тестового параметра – это может быть числовое значение или вектор символов
validRange задает область значений входных значений для тестового параметра — это может быть 1x2 вектор числовых значений с верхними и более низкими областями значений или массивом ячеек char (Перечисление).

Параметр char типа становится полезным при определении системных условий. Например, в системе связи, параметр Канала может быть задан так, чтобы он принял значения, такие как 'Рейли', ‘Rician’ или ‘AWGN’. В зависимости от значения char Канала система может пропустить передаваемые данные через различный канал. Это позволяет симуляцию системы по различным сценариям канала.

Если система указывает тестовый параметр, названный ‘X’ затем, система должна также содержать читаемое свойство, названное ‘X’. В противном случае процесс регистрации выдает ошибку. Этот процесс гарантирует, что вызов метода getTestParameter в режиме отладки возвращает значение, сохраненное соответствующим свойством.

Регистрация тестовых зондов

Протестируйте журнал зондов данные моделирования Тестовое Консольное использование Коэффициента ошибок для вычисления тестовых метрик, таких как: количество ошибок, количество передач и коэффициент ошибок. К данным логов в зонд ваша система связи должна указать зонд к Тестовой Консоли Коэффициента ошибок.

Вы указываете тестовый зонд к Тестовой Консоли Коэффициента ошибок с помощью метода registerTestProbe(sys,name,description).

sys представляет указатель на пользовательский системный объект
name представляет имя тестового зонда
description содержит информацию о тестовых зондах; полезный для указания, для чего используется зонд. Вход описания является дополнительным.

Можно задать произвольное число зондов, чтобы регистрировать тестовые данные в нескольких точках в системе.

Запись Метода Setup. Тестовая Консоль Коэффициента ошибок вызывает метод setup в начале симуляций для каждой новой точки развертки. Точка развертки является одним из нескольких наборов параметров симуляции, для которых будет моделироваться система. Используя метод getTestParameter системы под тестом, метод setup запрашивает текущие значения развертки симуляции от Тестовой Консоли Коэффициента ошибок и устанавливает различные компоненты системы соответственно. Метод setup устанавливает систему на условия, которые генерируют текущие тестовые значения развертки параметра.

Запись метода setup для каждой системы связи, которую вы создаете, не необходима. Метод setup является дополнительным.

Запись Метода Сброса. Используйте метод reset, чтобы сбросить состояния различных компонентов системы, такие как: объекты, буферы данных или системные флаги. Тестовая Консоль Коэффициента ошибок вызывает метод reset системы:

в начале симуляций для новой точки развертки. (Это условие происходит, когда вы устанавливаете ResetMode Тестовой Консоли Коэффициента ошибок “Сбрасывать в новой точке симуляции'.)
в каждой итерации симуляции. (Это условие происходит, когда вы устанавливаете ResetMode Тестовой Консоли Коэффициента ошибок 'Сбрасывать в каждой итерации’.)

Запись метода reset для каждой системы связи, которую вы создаете, не обязательна. Метод reset является дополнительным.

Запись Метода Выполнения. Запишите метод run для каждой системы связи, которую вы создаете. Метод run включает базовую функциональность системы под тестом. В каждой итерации симуляции Тестовая Консоль Коэффициента ошибок вызывает метод run системы под тестом.

При разработке системы связи гарантируйте во время выполнения, что система устанавливает компоненты на текущие тестовые значения развертки параметра симуляции. В зависимости от вашего уникального проекта, во время выполнения, систему связи:

тестовые воздействия запросов от тестовой консоли с помощью метода getInput
логарифмические тестовые данные к его тестовым зондам с помощью метода setTestProbeData
логарифмические пользовательские данные к тестовой консоли с помощью метода setUserData
Несмотря на то, что рекомендуется, чтобы вы сделали это во время установки, система может также запросить текущие значения развертки симуляции с помощью метода getTestParameter.

Методы, разрешающие вам связываться с тестовой консолью коэффициента ошибок во время выполнения симуляции

Получение тестовых воздействий от тестовой консоли коэффициента ошибок
Получение текущего значения развертки симуляции зарегистрированного тестового параметра
Журналирование тестовых данных к зарегистрированному тестовому зонду
Регистрация пользовательских данных к тестовой консоли

Получение Тестовых воздействий От Тестовой Консоли Коэффициента ошибок. Во времени симуляции система связи, которую вы разрабатываете, может запросить входные данные к Тестовой Консоли Коэффициента ошибок. Чтобы запросить конкретный тип входных данных, система под тестом должна указать определенный входной тип к Тестовой Консоли Коэффициента ошибок. Система под тестом вызывает getInput (obj, inputName) метод, чтобы запросить тестовые воздействия к тестовой консоли.

obj представляет указатель Тестовой Консоли Коэффициента ошибок
inputName представляет вход, который система под тестом получает от Тестовой Консоли Коэффициента ошибок

Для Тестовой Консоли Коэффициента ошибок 'NumTransmissions' или 'RandomDiscreetSource' являются приемлемыми выборами для inputName.

Система под тестом обеспечивает следующие входные параметры:

'NumTransmissions' - вызов метода getInput возвращает длину кадра. Сама система ответственна за генерацию кадра данных с помощью источника данных.
'RandomIntegerSource' - вызов метода getInput возвращает вектор символов с длиной, которую задает свойство Error Rate Test Console FrameLength. Если система указывает этот исходный тип, то это должно также указать тестовый параметр под названием 'M', который соответствует порядку модуляции.

Получение Текущего Значения Развертки Симуляции Зарегистрированного Тестового Параметра. Для каждой итерации симуляции система под тестом может потребовать текущих значений развертки симуляции от зарегистрированных тестовых параметров. Чтобы получить эти значения из консоли Error Rate Test, система под тестом вызывает метод getTestParameter(sys,name).

Журналирование Тестовых данных к Зарегистрированному Тестовому Зонду. Во времени симуляции система под тестом может данные логов к зарегистрированному тестовому зонду использование метода setTestProbeData(sys,name,data).

sys представляет указатель на систему
name представляет имя зарегистрированного тестового зонда
data представляет данные тестовые журналы Тестовой Консоли Коэффициента ошибок.

Регистрация Пользовательских Данных К Тестовой Консоли. Во времени симуляции система под тестом может регистрировать пользовательские данные к Тестовой Консоли Коэффициента ошибок путем вызова метода setUserData. Эти пользовательские данные передают непосредственно определенным пользовательским метрическим функциям калькулятора. Регистрируйте пользовательские данные к Тестовой Консоли Коэффициента ошибок можно следующим образом:

setUserData(sys,data)

sys представляет указатель на систему
data представляет данные тестовые журналы Тестовой Консоли Коэффициента ошибок.

Режим отладки

Система, которая расширяет testconsole. Класс SystemBasicAPI может запуститься отдельно без потребности присоединить его к тестовой консоли. Этот сценарий упоминается как режим отладки. Режим отладки полезен при оценке или отладке кода для системы, которую вы разрабатываете. Например, если вы задаете точки останова при разработке системы, можно запустить систему в режиме отладки и подтвердить, что система запускается без ошибок или предупреждений.

Реализация входной функции генератора по умолчанию для режима отладки

Реализация Входной Функции Генератора По умолчанию Для Режима отладки. Если ваша система указывает тестовое воздействие и вызывает метод getInput во время выполнения симуляции затем для него, чтобы запуститься в режиме отладки, система должна реализовать входную функцию генератора по умолчанию. Этот метод должен возвратить вход, конгруэнтный тестовой консоли.

input = generateDefaultInput(obj)

Запустите симуляции Используя тестовую консоль коэффициента ошибок

Создание тестовой консоли
Присоединение системы к тестовой консоли коэффициента ошибок
Определение условий симуляции
Регистрация тестовой точки
Получение тестовой информации
Выполнение симуляции
Получение результатов и отображение на графике данных
Парсинг и графический вывод результатов для нескольких симуляций параметра

Рабочие симуляции с Тестовой Консолью Коэффициента ошибок включают следующие задачи:

Создание тестовой консоли
Присоединение системы
Определение условий симуляции
- Определение критерия остановки
- Определение режима итерации
- Определение режима сброса
- Определение значений развертки
Регистрация тестовых точек
Рабочие симуляции
Получение результатов и графического вывода

Создание Тестовой Консоли. Вы создаете тестовую консоль одним из следующих способов:

h = commtest.ErrorRate возвращает тестовую консоль коэффициента ошибок, h. Тестовая консоль коэффициента ошибок запускает симуляции системы под тестом, чтобы получить коэффициенты ошибок.
h = commtest.ErrorRate(sys) возвращает тестовую консоль коэффициента ошибок, h, с присоединенной системой под тестом, sys.
h = commtest.ErrorRate(sys,'PropertyName',PropertyValue,...) возвращает тестовую консоль коэффициента ошибок, h, с присоединенной системой под тестом, sys. Каждое заданное свойство, 'PropertyName', установлено в заданное значение, PropertyValue.
h = commtest.ErrorRate('PropertyName',PropertyValue,...) возвращает тестовую консоль коэффициента ошибок, h, с каждым заданным свойством 'PropertyName', набором к заданному значению, PropertyValue.

Присоединение Системы к Тестовой Консоли Коэффициента ошибок. Вы присоединяете систему к Тестовой Консоли Коэффициента ошибок, чтобы запустить симуляции и получить данные о коэффициенте ошибок. Существует два способа присоединить систему к Тестовой Консоли Коэффициента ошибок.

Чтобы присоединить систему к Тестовой Консоли Коэффициента ошибок, введите следующее в командной строке MATLAB:
attachSystem(testConsole, mySystem)
Чтобы присоединить систему во время создания Тестовой Консоли Коэффициента ошибок, смотрите Создание Тестовой Консоли.
mySystem является именем системы под тестом

Если система под тестом A в настоящее время присоединена к Тестовому Консольному H1 Коэффициента ошибок, и вы вызываете attachSystem(H2,A), то отсоединения от H1 и присоединений к Тестовому Консольному H2 Коэффициента ошибок. Это заставляет систему отображать предупреждающее сообщение, утверждая, что она отсоединилась от H1 и присоединила к H2.

Определение условий симуляции

Остановите критерий

Тестовая Консоль Коэффициента ошибок управляет критерием остановки симуляции с помощью свойства SimulationLimitOption. Вы задаете критерий, чтобы остановить симуляцию при достижении или определенного количества передач или определенного количества ошибок.

Свойство Setting SimulationLimitOption к 'Количеству передач’ останавливает симуляцию для каждой точки параметра развертки, когда Тестовая Консоль Коэффициента ошибок считает количество передач заданным в MaxNumTransmissions
Свойство Setting SimulationLimitOption к 'Количеству ошибок' останавливает симуляцию для точки параметра развертки, когда Тестовая Консоль Коэффициента ошибок считает количество ошибок заданным в MinNumErrors. Свойство ErrorCountTestPoint должно быть установлено в имя зарегистрированной тестовой точки, содержащей ошибочное количество, сравнивающееся со свойством MinNumErrors управлять продолжительностью симуляции.
Свойство Setting SimulationLimitOption к 'Количеству ошибок или передач’ останавливает симуляцию для каждой точки параметра развертки, когда Тестовая Консоль Коэффициента ошибок завершает количество передач, заданных в MaxNumTransmissions или при получении количества ошибок, заданных в MinNumErrors, какой бы ни происходит сначала.

Режим итерации

Режим итерации задает способ, которым Тестовая Консоль Коэффициента ошибок комбинирует тестовые значения развертки параметра, чтобы выполнить симуляции. Свойство IterationMode тестовой консоли управляет этим поведением.

Установка IterationMode к 'Комбинаторному' выполняет симуляции для всех возможных комбинаций зарегистрированных тестовых значений развертки параметра.
Установка IterationMode к 'Индексируемому' выполняет симуляции для всех индексируемых наборов значений развертки. Набор значений развертки ^ith состоит из элемента ^ith от каждого вектора значения развертки для каждого зарегистрированного тестового параметра. Все векторы значения развертки должны иметь равную длину, за исключением тех, которые являются единичной длиной.

Определение и получение значений развертки

Тестовая Консоль Коэффициента ошибок выполняет симуляции для набора точек развертки, которые состоят из комбинаций значений развертки, заданных для каждого зарегистрированного тестового параметра. Путем тестовые консольные точки развертки форм зависят от настроек IterationMode. Режим итерации задает путь, которым значения развертки для различных тестовых параметров объединяются, чтобы произвести результаты симуляции.

Используя метод setTestParameterSweepValues, вы задаете значения развертки для каждого тестового параметра, который система под тестом указывает к Тестовой Консоли Коэффициента ошибок.

setTestParameterSweepValues(obj,name,value)

где

obj представляет указатель на Тестовую Консоль Коэффициента ошибок.
name представляет имя зарегистрированного тестового параметра (это имя должно соответствовать тестовому параметру, указанному системой под тестом, или ошибка происходит),
value представляет значения развертки, которые вы задаете для тестового параметра, названного 'именем'. В зависимости от приложения значения развертки могут быть вектором с числовыми значениями или массивом ячеек символов. Тестовая консоль выдает ошибку, при попытке установить значения развертки, которые являются вне заданной допустимой области значений для тестового параметра (допустимые области значений заданы системой при присоединении к тестовой консоли).

Вы получаете список тестовых параметров, указанных системой под тестом с помощью метода info Тестовой Консоли Коэффициента ошибок.

Вы получаете значения развертки для определенного зарегистрированного тестового параметра с помощью метода getTestParameterSweepValues Тестовой Консоли Коэффициента ошибок. Вы получаете допустимые области значений определенного зарегистрированного тестового параметра с помощью метода getTestParameterValidRanges Тестовой Консоли Коэффициента ошибок.

Если вы не задаете значения развертки для конкретного тестового параметра, Тестовой Консоли Коэффициента ошибок. всегда использует значение по умолчанию параметра, чтобы запустить симуляции. (Значения по умолчанию для тестовых параметров заданы системой при присоединении к тестовой консоли в регистрационное время.)

Сбросьте режим

Вы управляете критериями сброса системы под тестом с помощью свойства SystemResetMode Тестовой Консоли Коэффициента ошибок.

Установка SystemResetMode 'Сбросить в новой точке симуляции' сбрасывает систему под тестовым сбросом в начале итераций для новой точки развертки симуляции.
Установка SystemResetMode 'Сбросить в каждой итерации' сбрасывает систему под тестом при каждой симуляции.

Регистрация Тестовой точки. Вы получаете результаты коэффициента ошибок в различных точках в системе под тестом путем определения уникальных тестовых точек. Каждая тестовая точка группирует пару зондов, которые система под тестом использует для данных логов и Тестового Консольного использования Коэффициента ошибок, чтобы получить данные. В порядке создать тестовую точку для пары зондов, зонды должны быть указаны к Тестовой Консоли Коэффициента ошибок.

Тестовая Консоль Коэффициента ошибок вычисляет коэффициенты ошибок путем сравнения доступных данных в паре зондов.

Тестовые точки содержат ошибку и счета передачи для каждой симуляции точки развертки.

Информационные отображения метода, какие тестовые точки указаны к тестовой консоли.

registerTestPoint(h, name, actprobe, expprobe) указывает новую тестовую точку с именем, именем, к тестовой консоли коэффициента ошибок, h.

Тестовая точка должна содержать пару зарегистрированных тестовых зондов actprobe и expprobe, данные которого сравнятся, получают значения коэффициента ошибок. actprobe содержит фактические данные, и expprobe содержит ожидаемые данные. Коэффициенты ошибок будут вычислены с помощью функции калькулятора коэффициента ошибок по умолчанию, которая просто выполняет непосредственные сравнения векторов данных, доступных в зондах.

registerTestPoint(h, name, actprobe, expprobe, fcnhandle) добавляет указатель на функцию, fcnhandle, который указывает на пользовательскую ошибочную функцию калькулятора, которая будет использоваться вместо функции по умолчанию, чтобы сравнить данные в зондах actprobe и exprobe, получить результаты коэффициента ошибок.

Запись пользовательской ошибочной функции калькулятора

Пользовательская ошибочная функция калькулятора должна выполнить следующий синтаксис:

[ecnt tcnt] = functionName(act, exp, udata), где ecnt вывод соответствует ошибочному количеству и tcnt вывод, является количеством передач, используемых, чтобы получить ошибочное количество. Входные параметры act и exp соответствуют фактическим и ожидаемым данным. Тестовая консоль коэффициента ошибок установит эти входные параметры на доступные данные в паре зондов тестовой точки actprobe и expprobe, ранее упомянутый. udata является пользовательским вводом данных, который система под тестом может передать тестовой консоли во время выполнения с помощью метода setUserData. udata может содержать данные, необходимые, чтобы вычислить ошибки, такие как задержки, буферы данных, и так далее. Тестовая консоль коэффициента ошибок передаст те же пользовательские данные, регистрируемые системой под тестом к ошибочным функциям калькулятора всех зарегистрированных тестовых точек. Вы вызываете информационный метод, чтобы видеть имена зарегистрированных тестовых точек и функций калькулятора коэффициента ошибок, сопоставленных с ними, и видеть имена зарегистрированных тестовых зондов.

Получение Тестовой информации. Возвращает отчет текущих тестовых консольных настроек.

информация (h) отображения:

Протестируйте консольное имя
Система под тестовым именем
Доступные тестовые воздействия
Зарегистрированные тестовые воздействия
Зарегистрированные тестовые параметры
Зарегистрированные тестовые зонды
Зарегистрированные тестовые точки
Метрические функции калькулятора
Протестируйте метрики

Выполнение Симуляции. Вы запускаете симуляции путем вызова метода run Тестовой Консоли Коэффициента ошибок.

run(testConsole) запускает конкретное количество итераций присоединенной системы под тестом для заданного набора значений параметров. Если лицензия Parallel Computing Toolbox™ доступна, и parpool открыт, то можно распределить итерации среди доступного количества рабочих.

Получение Результатов и Отображение на графике Данных. Вызовите метод getResults тестовой консоли коэффициента ошибок, чтобы получить результаты испытаний.

r = getResults(testConsole) возвращает результаты симуляции, r, для тестовой консоли, testConsole. r является объектом типа testconsole.Results и содержит данные моделирования для всех зарегистрированных тестовых точек.

Вы вызываете метод getData объекта результатов r, чтобы получить данные о результатах симуляции. Вы вызываете график и метод semilogy объекта r результатов отобразить данные о результатах на графике. Смотрите testconsole.Results для получения дополнительной информации.

Парсинг и Графический вывод Результатов для Нескольких Симуляций Параметра. Файл DPSKModulationTester.mat содержит Тестовую Консоль Коэффициента ошибок с системой модуляции DPSK. Эта система задает три тестовых параметра:

Энергия, подведенная к долоту к шумовой степени спектральное отношение плотности, EbNo (в децибелах)
Порядок модуляции, M
Максимальный эффект Доплера, MaxDopplerShift (в герц)

Эти параметры имеют следующие значения развертки:

EbNo = [-2:4] дБ
M = [2 4 8 16]
MaxDopplerShift = [0 0.001 0.09] Гц

Поскольку симуляции обычно занимают много времени, чтобы запуститься, симуляция была запущена оффлайн. Файл DPSKModulationTester.mat содержит сохраненную Тестовую Консоль Коэффициента ошибок с сохраненными результатами. Симуляции были запущены, чтобы получить по крайней мере 2 500 ошибок и 5e6 передачи кадра на точку симуляции.

Загрузите результаты симуляции путем ввода следующего в командной строке MATLAB:

load DPSKModulationTester.mat

Чтобы проанализировать и построить результаты для нескольких симуляций параметра, выполните следующие шаги:

Используя метод getSweepParameterValues, отобразите значения параметров развертки, используемые в симуляции для каждого тестового параметра. Например, вы отображаете значения развертки для MaxDopplerShift путем ввода:
```
getTestParameterSweepValues(testConsole,'MaxDopplerShift') 
```
MATLAB возвращает следующий результат:
```
ans =

         0    0.0010    0.0900
```

Доберитесь результаты возражают, что синтаксические анализы и строят результаты симуляции путем ввода следующего в командной строке:

DPSKResults = getResults(testConsole)

MATLAB возвращает следующий результат:

DPSKResults =

        TestConsoleName: 'commtest.ErrorRate'
    SystemUnderTestName: 'commexample.DPSKModulation'
          IterationMode: 'Combinatorial'
              TestPoint: 'BitErrors'
                 Metric: 'ErrorRate'
         TestParameter1: 'EbNo'
         TestParameter2: 'None'

Используйте метод setParsingValues, чтобы включить графический вывод результатов коэффициента ошибок по сравнению с Eb/No для порядка модуляции 4 и максимального эффекта Доплера 0,001 Гц. Для этого введите following:.
```
setParsingValues(DPSKResults,'M',4,'MaxDopplerShift',0.001)
```
Используйте the getParsingValues метод, чтобы проверить текущие настройки значений парсинга:
```
getParsingValues(DPSKResults)
```
MATLAB возвращает следующее:
```
ans =

               EbNo: -2
                  M: 4
    MaxDopplerShift: 1.0000e-003
```
Если не заданный, значение парсинга для тестового параметра значения по умолчанию к его первому значению развертки. В этом примере первое значение развертки для EbNo равняется-2 дБ. Однако в этом примере, TestParameter1 установлен в EbNo; поэтому, Тестовая Консоль Коэффициента ошибок строит результаты для всех значений развертки EbNo, не только для значения, перечисленного методом getParsingValues.
Получите график логарифмической шкалы частоты ошибок по битам по сравнению с Eb/No для порядка модуляции 4 и максимального эффекта Доплера 0,001 Гц:
```
semilogy(DPSKResults)
```
MATLAB генерирует следующую фигуру.
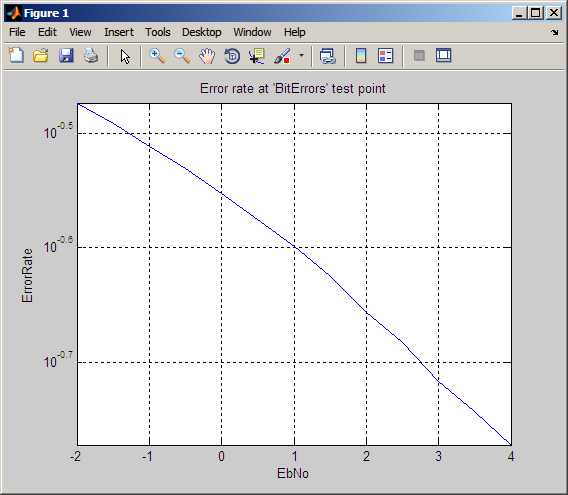
Установите свойство TestParameter2 объекта результатов к 'MaxDopplerShift'. Эта установка включает графический вывод нескольких кривых коэффициента ошибок по сравнению с Eb/No для каждого значения развертки максимального эффекта Доплера.
DPSKResults.TestParameter2 = 'MaxDopplerShift';
Получите графики логарифмической шкалы частоты ошибок по битам по сравнению с Eb/No для порядка модуляции 2 в каждом из максимальных значений развертки эффекта Доплера.
```
setParsingValues(DPSKResults,'M',2)
semilogy(DPSKResults)
```
MATLAB генерирует следующую фигуру.
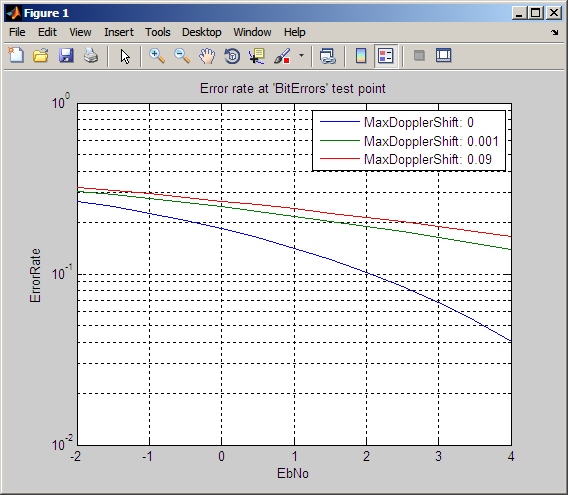
Получите тот же тип кривых как на предыдущем шаге, но теперь для порядка модуляции 16.
```
setParsingValues(DPSKResults,'M',16)
semilogy(DPSKResults)
```
MATLAB генерирует следующую фигуру.
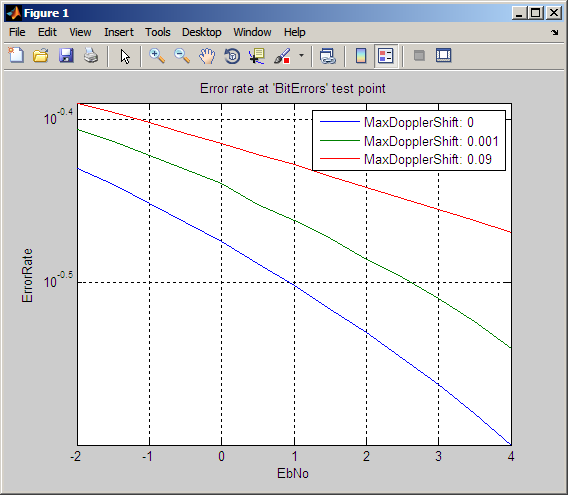
Получите графики коэффициента ошибок по сравнению с порядком модуляции для каждого значения развертки Eb/No установкой TestParameter1, равной M и TestParameter2, равному EbNo. Можно построить результаты для случая, когда максимальный эффект Доплера составляет 0 Гц при помощи метода setParsingValues:
```
DPSKResults.TestParameter1 = 'M';
DPSKResults.TestParameter2 = 'EbNo';
setParsingValues(DPSKResults, 'MaxDopplerShift',0)
semilogy(DPSKResults)
```
MATLAB генерирует следующую фигуру.

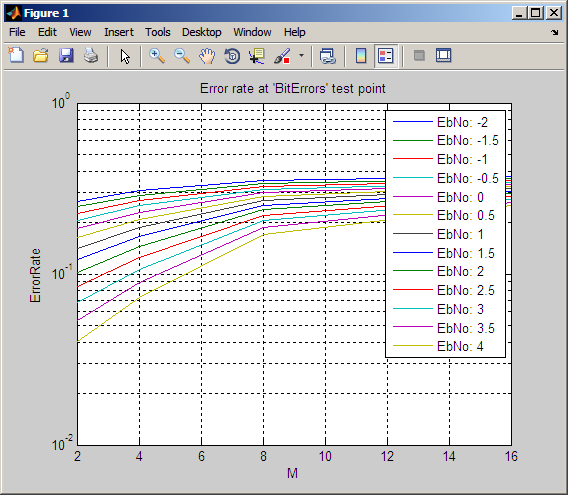
Получите матрицу данных со значениями частоты ошибок по битам, ранее построенными путем ввода следующего:

BERMatrix = getData(DPSKResults)

MATLAB возвращает следующий результат:

BERMatrix =

  Columns 1 through 7

    0.2660    0.2467    0.2258    0.2049    0.1837    0.1628    0.1418
    0.3076    0.2889    0.2702    0.2504    0.2296    0.2082    0.1871
    0.3510    0.3384    0.3258    0.3120    0.2983    0.2837    0.2685
    0.3715    0.3631    0.3535    0.3442    0.3350    0.3246    0.3147

  Columns 8 through 13

    0.1217    0.1022    0.0844    0.0677    0.0534    0.0406
    0.1658    0.1451    0.1254    0.1065    0.0890    0.0728
    0.2531    0.2369    0.2204    0.2042    0.1874    0.1704
    0.3044    0.2945    0.2839    0.2735    0.2626    0.2512

Строки матрицы соответствуют значениям тестового параметра, заданного свойством TestParameter1, M. Столбцы соответствуют значениям тестового параметра, заданного свойством TestParameter2, EbNo.

Постройте результаты как 3-D график данных путем ввода следующего:
```
surf(DPSKResults) 
```
MATLAB генерирует следующий график:
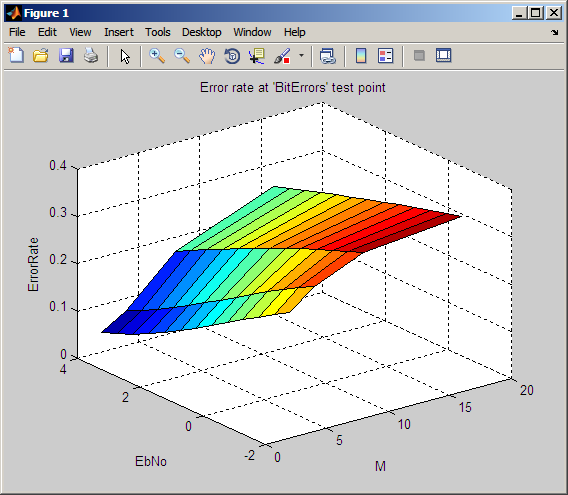
В этом случае параметр, заданный свойством TestParameter1, M, управляет осью X и параметром, заданным свойством TestParameter2, EbNo, управляет осью Y.

Симуляции Частоты ошибок по битам Для Различных Стоимостей заказов Eb/No и Модуляции

Задачи для рабочих симуляций частоты ошибок по битам для различного En/No и стоимостей заказов модуляции.

Загрузите тестовую консоль коэффициента ошибок
Запустите симуляцию и получите результаты
Сгенерируйте окно рисунка результатов коэффициента ошибок
Идите параллельно симуляции Используя программное обеспечение Parallel Computing Toolbox
Создайте системный файл и присоедините его к тестовой консоли
Сконфигурируйте тестовую консоль коэффициента ошибок и запустите симуляцию
Оптимизируйте производительность системы Используя параметризованные симуляции

Загрузите Тестовую Консоль Коэффициента ошибок. Тестовая Консоль Коэффициента ошибок является инструментом симуляции для получения результатов коэффициента ошибок. Программное обеспечение MATLAB включает файл данных для использования с Тестовой Консолью Коэффициента ошибок. Вы будете использовать файл данных при выполнении шагов этого примера. Файл данных содержит объект Error Rate Test Console с закодированной системой модуляции присоединенного Грэя. Эта Тестовая Консоль Коэффициента ошибок в качестве примера сконфигурирована, чтобы запустить симуляции частоты ошибок по битам для различного EbNo и порядка модуляции, или M, значений.

Загрузите файл, содержащий Тестовую Консоль Коэффициента ошибок, и присоединил закодированную систему модуляции Грэя. В командной строке MATLAB, введите:
```
load GrayCodedModTester_EbNo_M
```
Исследуйте тестовую консоль путем отображения ее свойств. В командной строке MATLAB, введите:
```
testConsole
```
MATLAB возвращает следующий выходной параметр:
```
testConsole =

                   Description: 'Error Rate Test Console'
           SystemUnderTestName: 'commexample.GrayCodedMod_EbNo_M'
                 IterationMode: 'Combinatorial'
               SystemResetMode: 'Reset at new simulation point'
         SimulationLimitOption: 'Number of errors or transmissions'
    TransmissionCountTestPoint: 'DemodBitErrors'
           MaxNumTransmissions: 100000000
           ErrorCountTestPoint: 'DemodBitErrors'
                  MinNumErrors: 100
```
Заметьте, что SystemUnderTest является закодированной системой модуляции Грэя. Поскольку SimulationLimitOption является 'Количеством ошибки или передачи', выполнения симуляции до достижения 100 ошибок или 1e8 биты.

Запустите Симуляцию и Получите Результаты. В этом примере вы используете tic и toc, чтобы сравнить время выполнения симуляции.

Запустите симуляцию, с помощью tic и команд toc, чтобы измерить время симуляции. В командной строке MATLAB, введите:
```
tic; run(testConsole); toc
```
MATLAB возвращает выходной параметр, подобный следующему:
```
Running simulations...
Elapsed time is 174.671632 seconds.
```

Получите результаты симуляции с помощью метода getResults путем ввода следующего в командной строке MATLAB:

grayResults = getResults(testConsole)

MATLAB возвращает следующий выходной параметр:

grayResults =

        TestConsoleName: 'commtest.ErrorRate'
    SystemUnderTestName: 'commexample.GrayCodedMod_EbNo_M'
          IterationMode: 'Combinatorial'
              TestPoint: 'DemodBitErrors'
                 Metric: 'ErrorRate'
         TestParameter1: 'EbNo'
         TestParameter2: 'None'

В следующем разделе вы используете объект результатов получить ошибочные значения и кривые коэффициента ошибок графика.

Сгенерируйте Окно рисунка Результатов Коэффициента ошибок. Метод semilogy генерирует фигуру, содержащую кривые коэффициента ошибок для тестовой точки битовой ошибки демодулятора (DemodBitErrors) закодированной системы модуляции Грэя. Следующие данные показывают Коэффициент ошибок и _Эба ни по _Какой кривой для тестовой точки битовых ошибок демодулятора. Эта тестовая точка собирает битовые ошибки путем сравнения битов системные передачи с битами, которые она получает. Ось X отображает свойство TestParameter1 grayResults, который содержит значения EbNo.

Сгенерируйте фигуру путем ввода следующего в командной строке MATLAB:
```
semilogy(grayResults)
```
Этот скрипт генерирует следующую фигуру.
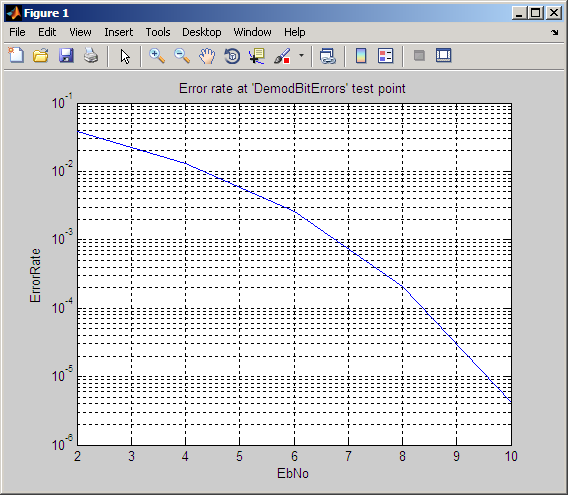
Установите свойство TestParameter2 на M. В командной строке MATLAB, введите:
```
grayResults.TestParameter2 = 'M'
```
Ранее симуляция запускалась для нескольких значений порядка (M) модуляции. Ось X отображает свойство TestParameter1 grayResults, который содержит значения EbNo. Несмотря на то, что симуляция запустилась для нескольких значений M, это выполнение содержит данные для M=2.
Постройте несколько кривых коэффициента ошибок путем ввода следующего в командной строке MATLAB.
```
semilogy(grayResults)
```
Этот скрипт генерирует следующую фигуру.

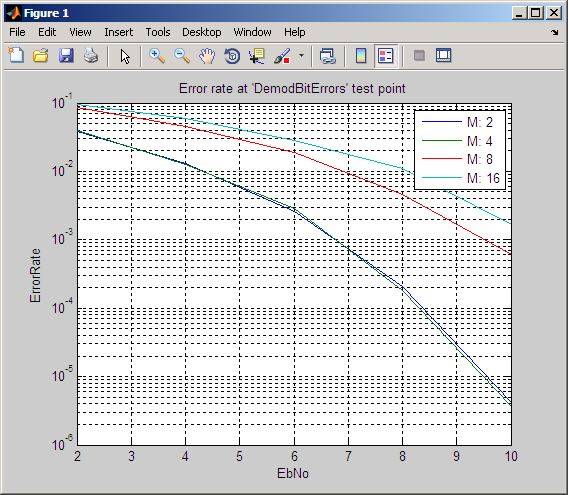
Run Parallel Simulations Using Parallel Computing Toolbox Software. Если у вас есть пользовательская лицензия Parallel Computing Toolbox, и вы создаете parpool, тестовая консоль запускает симуляцию параллельно. Этот подход уменьшает время вычислений.

Примечание

Если у вас нет пользовательской лицензии Parallel Computing Toolbox, вы не можете выполнить этот раздел примера.

Если вы имеете лицензию Parallel Computing Toolbox, запускаете следующую команду, чтобы запустить ваше значение по умолчанию parpool:
```
mypool = parpool()
```
Если у вас есть многоядерный компьютер, то значение по умолчанию parpool использует ядра в качестве рабочих.
Используя рабочих, запустите симуляцию. В командной строке MATLAB, введите:

tic; run(testConsole); toc

MATLAB возвращает выходной параметр, подобный следующему:

4 workers available for parallel computing. Simulations ...,
will be distributed among these workers.
Running simulations...
Elapsed time is 87.449652 seconds.

Заметьте что выполнения симуляции, больше чем в три раза более быстрые, чем в предыдущем разделе.

Создайте Системный файл и Присоединение Это к Тестовой Консоли. В предыдущих разделах вы использовали закодированный системный файл модулятора существующего Грэя, чтобы сгенерировать данные. В этом разделе вы создаете системный файл и затем присоединяете его к Тестовой Консоли Коэффициента ошибок.

Этот пример обрисовывает в общих чертах задачи, необходимые для преобразования унаследованного кода к системному файлу, который можно присоединить к Тестовой Консоли Коэффициента ошибок. Используйте commdoc_gray в качестве отправной точки для вашего системного файла. Файлы, которые вы используете в этом разделе примера, находятся в следующей папке:

matlab\help\toolbox\comm\examples

Скопируйте систему основной шаблон API, SystemBasicTemplate.m, как MyGrayCodedModulation.m.
Переименуйте ссылки на имя системы в файле. Во-первых, переименуйте системное определение путем изменения имени класса на MyGrayCodedModulation. Замените следующие строки, строки 1 и 2, файла:
```
classdef SystemBasicTemplate < testconsole.SystemBasicAPI
%SystemBasicTemplate Template for creating a system
```
с этими строками:
```
classdef MyGrayCodedModulation < testconsole.SystemBasicAPI
%MyGrayCodedModulation Gray coded modulation system
```

Переименуйте конструктора, заменив:

function obj = SystemBasicTemplate
%SystemBasicTemplate Construct a system

function obj = MyGrayCodedModulation
%MyGrayCodedModulation Construct a Gray coded modulation system

Введите описание для своей системы. Обновите параметр obj.Description со следующей информацией:
```
obj.Description = 'Gray coded modulation';
```
Поскольку вы не используете reset и методы setup для этой системы, оставляете эти методы пустыми.
Скопируйте строки 12–44 от commdoc_gray.m до тела метода run.
Скопируйте Строки 54–57 от commdoc_gray.m до тела метода run.
Измените EbNo на тестовый параметр. Это изменение позволяет системе получать значения EbNo из Тестовой Консоли Коэффициента ошибок. Как тестовый параметр, EbNo становится переменной, которая позволяет симуляциям запускаться для различных значений. Найдите следующую строку синтаксиса в файле:
```
EbNo = 10; % In dB
```
Замените его на:
```
EbNo = getTestParameter(obj,'EbNo');
```
Добавьте порядок модуляции, M, как новый тестовый параметр для симуляции. Найдите следующий синтаксис:
```
 M = 16;                     % Size of signal constellation
```
Замените его на:
```
M = getTestParameter(obj,'M');
```
Укажите тестовые параметры к тестовой консоли.
- Объявите EbNo как тестовый параметр путем размещения следующей строки кода в тело метода register:
```
registerTestParameter(obj,'EbNo',0,[-50 50]);
```
  Значения по умолчанию параметра к 0 дБ и могут принять значения между-50 дБ и 50 дБ.
- Объявите M как тестовый параметр путем размещения следующей строки кода в тело метода register:
```
registerTestParameter(obj,'M',16,[2 1024]);
```
  Значения по умолчанию параметра к 16 Модуляциям QAM и могут принять значения от 2 до 1 024.
Добавьте EbNo и M к тестовому списку параметров в файле MyGrayCodedModulationFile.
```
 % Test Parameters
    properties
        EbNo = 0;
  		 M = 16;
    end
```
Это добавляет EbNo и M к возможному тестовому списку параметров. Значения по умолчанию EbNo к значению 0 дБ. M значения по умолчанию к значению 16.
Задайте тестовые местоположения зонда в методе run. В этом примере вы вычисляете сквозной коэффициент ошибок. Это вычисление требует переданных битов и полученных битов. Добавьте один зонд для получения переданных битов и одного зонда для полученных битов.
- Найдите случайный потоковый код создания двоичных данных путем поиска следующих строк:
```
% Create a binary data stream as a column vector.
  x = randi([0 1],n,1); % Random binary data stream
```
- Добавьте зонд, TxBits, после случайного потокового создания двоичных данных:
```
 % Create a binary data stream as a column vector.
 x = randi([0 1],n,1); % Random binary data stream
 setTestProbeData(obj,'TxBits',x);
```
  Этот код отправляет случайный поток двоичных данных, x, в тестовый TxBits.
- Найдите код демодуляции путем поиска следующих строк:
```
% Demodulate signal using 16-QAM.
z = demodulate(hDemod,yRx);
```
- Добавьте зонд, RxBits, после кода демодуляции.
```
% Demodulate signal using 16-QAM.
z = demodulate(hDemod,yRx);
setTestProbeData(obj,'RxBits',z);
```
Этот код отправляет, двоичный файл получил поток данных, z, к тестовому RxBits.

Укажите тестовые зонды к Тестовой Консоли Коэффициента ошибок, позволив получить данные из системы. Добавьте эти зонды в функциональный register(obj) путем добавления двух строк в метод register:

function register(obj)
% REGISTER Register the system with a test console
% REGISTER(H) registers test parameters and test probes of the
% system, H, with a test console.

            registerTestParameter(obj,'EbNo',0,[-50 50]);
					registerTestParameter(obj,'M',16,[2 1024]);
            registerTestProbe(obj,'TxBits')
            registerTestProbe(obj,'RxBits')
        end

Сохраните файл. Файл готов к употреблению с системой.
Создайте Серую закодированную систему модуляции. В командной строке MATLAB, введите:
```
mySystem = MyGrayCodedModulation
```
MATLAB возвращает следующий выходной параметр:
```
mySystem =

    Description: 'Gray coded modulation'
           EbNo: 0
	            M: 16
```

Создайте Тестовую Консоль Коэффициента ошибок путем ввода следующего в командной строке MATLAB:

testConsole = commtest.ErrorRate

Программное обеспечение MATLAB возвращает следующий выходной параметр:

testConsole =

                   Description: 'Error Rate Test Console'
           SystemUnderTestName: 'commtest.MPSKSystem'
                   FrameLength: 500
                 IterationMode: 'Combinatorial'
               SystemResetMode: 'Reset at new simulation point'
         SimulationLimitOption: 'Number of transmissions'
    TransmissionCountTestPoint: 'Not set'
           MaxNumTransmissions: 1000

Присоедините системный файл MyGrayCodedModulation к тестовой консоли коэффициента ошибок путем ввода следующего в командной строке MATLAB:
```
attachSystem(testConsole, mySystem)
```

Сконфигурируйте Тестовую Консоль Коэффициента ошибок и Выполнение Симуляция. Сконфигурируйте Тестовую Консоль Коэффициента ошибок, чтобы получить метрики коэффициента ошибок из присоединенной системы. Тестовая Консоль Коэффициента ошибок задает метрики как количество ошибок, количество передач и коэффициент ошибок.

В командной строке MATLAB, введите:
```
registerTestPoint(testConsole, 'DemodBitErrors', 'TxBits', 'RxBits');
```
Эта строка задает тестовую точку, DemodBitErrors, и сравнивает биты от зонда TxBits до битов от зонда RxBits. Тестовая Консоль Коэффициента ошибок вычислила метрики для этой тестовой точки.
Сконфигурируйте Тестовую Консоль Коэффициента ошибок, чтобы запустить симуляции для значений EbNo. Запустите на уровне 2 дБ и закончитесь на уровне 10 дБ, с размером шага 2 дБ и значениями M 2, 4, 8, и 16. В командной строке MATLAB, введите:
```
setTestParameterSweepValues(testConsole, 'EbNo', 2:2:10)
setTestParameterSweepValues(testConsole, 'M', [2 4 8 16])
```
Установите предел симуляции к количеству передач.
```
testConsole.SimulationLimitOption = 'Number of transmissions'
```
Определите максимальный номер передач к 1 000.
```
testConsole.MaxNumTransmissions = 1000
```
Сконфигурируйте Тестовую Консоль Коэффициента ошибок, таким образом, она использует тестовую точку битовой ошибки демодулятора для определения количества переданных битов.
```
testConsole.TransmissionCountTestPoint = 'DemodBitErrors'
```
Запустите симуляцию. В командной строке MATLAB, введите:
```
run(testConsole)
```
Получите результаты симуляции. В командной строке MATLAB, введите:
```
grayResults = getResults(testConsole)
```
Чтобы получить более точные результаты, запустите симуляции для данного минимального количества ошибок. В этом примере вы также ограничиваете количество битов симуляции так, чтобы симуляции не запускались неопределенно. В командной строке MATLAB, введите:
```
testConsole.SimulationLimitOption = 'Number of errors or transmissions';
testConsole.MinNumErrors = 100;
testConsole.ErrorCountTestPoint = 'DemodBitErrors';
testConsole.MaxNumTransmissions = 1e8;
testConsole
```
Запустите симуляцию путем ввода следующего в командной строке MATLAB.
```
run(testConsole);
```
Сгенерируйте новые результаты в Окне рисунка путем ввода следующего в командной строке MATLAB.
```
grayResults = getResults(testConsole);
grayResults.TestParameter2 = 'M'
semilogy(grayResults)
```
Этот скрипт генерирует следующую фигуру.

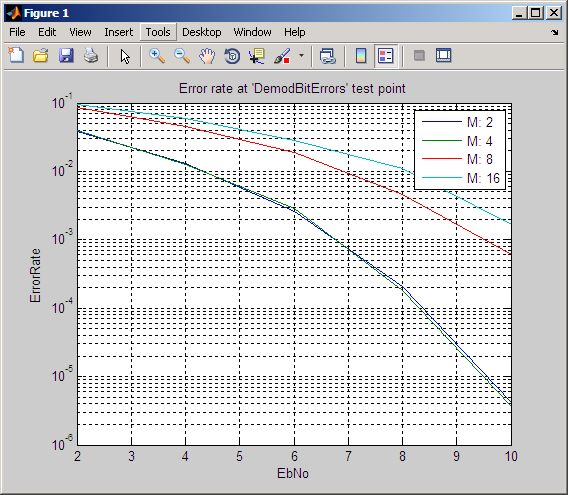
Оптимизируйте Производительность системы Используя Параметризованные Симуляции. В предыдущем примере система только использует метод run. Каждый раз, когда вызовы объектов метод run, который являются каждым 3e4 биты для этой симуляции, объект устанавливает значения ОСШ и M. Этот временной интервал включает: получение чисел от тестовой консоли, вычисление промежуточных значений и установка других переменных.

Напротив, система, которую основной API предоставляет методу setup, где Тестовая Консоль Коэффициента ошибок конфигурирует систему однажды для каждой точки симуляции. Это изменение уменьшает метод run от получения и установки параметров симуляции, таким образом уменьшая время симуляции.

Метод run системы также создает новый модулятор (hMod) и новый демодулятор (hDemod). Создание модулятора или демодулятора является намного более трудоемким, чем только изменение свойства этих объектов. Создайте модулятор и объект демодулятора однажды, когда система будет создана. Затем измените его свойства в методе настройки системы, чтобы ускорить симуляции.

Сохраните файл MyGrayCodedModulation как MyGrayCodedModulationOptimized.

В файле MyGrayCodedModulationOptimized замените имя конструктора и имя определения класса.

Найдите следующие строки кода:

classdef MyGrayCodedModulation < testconsole.SystemBasicAPI
%MyGrayCodedModulation Gray coded modulation system

Замените их на:

classdef MyGrayCodedModulationOptimized < testconsole.SystemBasicAPI
%MyGrayCodedModulationOptimized Gray coded modulation system

В MyGrayCodedModulationOptimized ﬁle замените имя конструктора.

Найдите следующие строки кода:

function obj = MyGrayCodedModulation
%MyGrayCodedModulation Construct a Gray coded modulation system

Замените их на:

function obj = MyGrayCodedModulationOptimized
%MyGrayCodedModulationOptimized Construct a Gray
%coded modulation system

Переместите определение уровня сверхдискретизации от метода run до метода setup.
```
nSamp = 1;                  % Oversampling rate
```
Переместите код, связанный с установкой M к методу setup. Сократите следующие строки из метода run и вставки к методу setup.
```
            M = getTestParameter(obj,'M');
            k = log2(M);                % Number of bits per symbol
```
В методе setup замените M на свойство объекта M.
```
obj.M = getTestParameter(obj,'M');
k = log2(obj.M);                % Number of bits per symbol
```
Это изменение обеспечивает доступ к значению M из метода run.
Переместите код, связанный с установкой EbNo к методу setup. Сократите следующие строки из метода run и вставки к методу setup.
```
EbNo = getTestParameter(obj,'EbNo');

SNR = EbNo + 10*log10(k) - 10*log10(nSamp);
```
В методе setup замените EbNo на свойство объекта EbNo. Это изменение обеспечивает доступ к значению EbNo из метода выполнения.
```
obj.EbNo = getTestParameter(obj,'EbNo');
SNR = obj.EbNo + 10*log10(k) - 10*log10(nSamp);
```
Создайте названный ОСШ новой внутренней переменной, чтобы сохранить расчетное значение ОСШ. Задайте свойство SNR как частную собственность; это не тестовый параметр. С этим изменением система вычисляет ОСШ в методе setup и получает доступ к нему из метода run. Добавьте следующие строки кода системный файл после блока Test Parameters.
```
%=================================================================
    % Internal variables
    properties (Access = private)
        SNR
    end
```
В методе setup замените ОСШ на ОСШ свойства объекта.
```
 obj.SNR = obj.EbNo + 10*log10(k) - 10*log10(nSamp);
```
В методе run замените M на obj. M и ОСШ с obj. ОСШ.
```
hMod = comm.RectangularQAMModulator(obj.M); % Create a 16-QAM modulator
yNoisy = awgn(yTx,obj.SNR,'measured'); 
```
Заметьте, что метод run создает модулятор QAM и демодулятор.

Переместите модулятор QAM и создание демодулятора из метода run. Переместите следующие строки от метода run до конструктора (т.е. метода под названием MyGrayCodedModulationOptimized)

%% Create Modulator and Demodulator
hMod = comm.RectangularQAMModulator(obj.M);     % Create a 16-QAM modulator
hMod.BitInput = true;                           % Accept bits as inputs
hMod.SymbolMapping = 'Gray';                    % Gray coded symbol mapping
hDemod = comm.RectangularQAMDemodulator(obj.M); % Create a 16-QAM demodulator
hDemod.BitOutput = true;                        % Output bits
hDemod.SymbolMapping = 'Gray';                  % Gray coded symbol mapping

Создайте частные свойства под названием Модулятор и Демодулятор, чтобы сохранить объекты демодулятора и модулятор.

% Internal variables
properties (Access = private)
SNR
Modulator
Demodulator
end

В методе конструктора замените hMod и hDemod со свойством объекта obj.Modulator и obj.Demodulator соответственно.

% Create a 16-QAM modulator
obj.Modulator = comm.RectangularQAMModulator(obj.M, ...
'BitInput',true,'SymbolMapping','Gray');
% Create a 16-QAM demodulator
obj.Demodulator = comm.RectangularQAMDemodulator(obj.M, ...
'BitOutput',true,'SymbolMapping','Gray');

В методе run замените hMod и hDemod со свойствами объектов obj.Modulator и obj.Demodulator.

y = modulate(obj.Modulator,x);
z = demodulate(obj.Demodulator,yRx);

Найдите область настройки ﬁle.

function setup(obj)
% SETUP Initialize the system
% SETUP(H) gets current test parameter value(s) from the test
% console and initializes system, H, accordingly.

Установите значение M модулятора и демодулятора путем добавления следующих строк кода в настройку.
```
obj.Modulator.M = obj.M;
obj.Demodulator.M = obj.M;
```
Сохраните ﬁle.
Создайте оптимизированную систему. В командной строке MATLAB, введите:
```
myOptimSystem = MyGrayCodedModulationOptimized
```
Создайте Тестовую Консоль Коэффициента ошибок и присоедините систему к тестовой консоли. В командной строке MATLAB введите:
```
testConsole = commtest.ErrorRate(myOptimSystem)
```
В командной строке MATLAB введите:
```
registerTestPoint(testConsole, 'DemodBitErrors', 'TxBits', 'RxBits');
```
Эта строка задает тестовую точку, DemodBitErrors, и сравнивает биты от зонда TxBits до битов от зонда RxBits. Тестовая Консоль Коэффициента ошибок вычислила метрики для этой тестовой точки.
Сконфигурируйте Тестовую Консоль Коэффициента ошибок, чтобы запустить симуляции для значений EbNo. Запустите на уровне 2 дБ и закончитесь на уровне 10 дБ, с размером шага 2 дБ и значениями M 2, 4, 8, и 16. В командной строке MATLAB введите:
```
setTestParameterSweepValues(testConsole, 'EbNo', 2:2:10)
setTestParameterSweepValues(testConsole, 'M', [2 4 8 16])
```
Сконфигурируйте Тестовую Консоль Коэффициента ошибок, таким образом, она использует тестовую точку битовой ошибки демодулятора для определения количества переданных битов.
```
testConsole.TransmissionCountTestPoint = 'DemodBitErrors'
```
Чтобы получить более точные результаты, запустите симуляции для данного минимального количества ошибок. В этом примере вы также ограничиваете количество битов симуляции так, чтобы симуляции не запускались неопределенно. В командной строке MATLAB введите:
```
testConsole.SimulationLimitOption = 'Number of errors or transmissions';
testConsole.MinNumErrors = 100;
testConsole.ErrorCountTestPoint = 'DemodBitErrors';
testConsole.MaxNumTransmissions = 1e8;
testConsole
```
Запустите симуляцию. В командной строке MATLAB введите:
```
tic; run(testConsole); toc
```
MATLAB возвращает следующую информацию:
```
Running simulations...
Elapsed time is 191.748359 seconds.
```
Заметьте, что эти изменения оптимизации уменьшают время выполнения симуляции приблизительно 10%.
Сгенерируйте новые результаты в Окне рисунка. В командной строке MATLAB введите:
```
grayResults = getResults(testConsole);
grayResults.TestParameter2 = 'M'
semilogy(grayResults) 
```
Этот скрипт генерирует следующую фигуру.

Документация