Настраивающий алгоритм ПИДа для линейной модели объекта управления
C = pidtune(sys,type)
C = pidtune(sys,C0)
C = pidtune(sys,type,wc)
C =
pidtune(sys,C0,wc)
C = pidtune(sys,...,opts)
[C,info]
= pidtune(...)
C = pidtune(sys,type)type для объекта sys. Если type задает одну степень свободы (1-DOF) ПИД-регулятор, то контроллер разработан для модульной обратной связи, как проиллюстрировано:
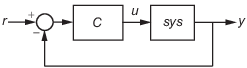
Если type задает две степени свободы (2-DOF) ПИД-регулятор, то pidtune разрабатывает контроллер 2-DOF как в обратной связи этого рисунка:
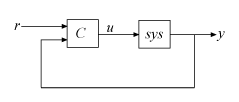
pidtune настраивает параметры ПИД-регулятора C, чтобы сбалансировать производительность (время отклика) и робастность (запасы устойчивости).
C = pidtune(sys,C0)C0. Если sys и C0 являются моделями дискретного времени, C имеет те же дискретные формулы интегратора как C0.
C = pidtune(sys,type,wc)C =
pidtune(sys,C0,wc)wc для первых 0 частот перекрестного соединения усиления дБ ответа разомкнутого цикла.
C = pidtune(sys,...,opts)pidtuneOptions, чтобы указать, что опция установила opts.
[ возвращает структуру данных C,info]
= pidtune(...)info, который содержит информацию об устойчивости с обратной связью, выбранной частоте перекрестного соединения коэффициента усиления разомкнутого контура и фактическом поле фазы.
|
Одно вход, модель динамической системы одно вывода объекта для проектирования контроллера.
Если объект имеет нестабильные полюса, и
необходимо использовать |
|
Тип контроллера контроллера, чтобы разработать, заданный как вектор символов. Термин controller type относится, к которому условия присутствуют в действии контроллера. Например, у контроллера PI есть только пропорциональное и интегральный термин, в то время как контроллер PIDF содержит пропорциональный, интегратор, и отфильтровал производные условия. Контроллеры 1-DOF
Контроллеры 2-DOF
Для получения дополнительной информации о ПИД-регуляторах 2-DOF обычно, см. Два ПИД-регулятора Степени свободы. Контроллеры 2-DOF с фиксированными весами заданного значения
Для более подробной информации о фиксированном весе заданного значения ПИД-регуляторы 2-DOF смотрите Типы ПИД-регулятора для Настройки. Форма контроллераКогда вы используете вход Если Для получения дополнительной информации о формах ПИД-регулятора и формулах, см.:
|
|
Свойства установки ПИД-регулятора разработанного контроллера, заданного как
|
|
Целевое значение для 0 усилений дБ перекрестно соединяет частоту настроенного ответа разомкнутого цикла. Задайте Увеличьте |
|
Набор опции, задающий дополнительные настраивающие опции для |
|
Контроллер разработан для Форма контроллера:
Тип контроллера:
Или в случае, однако, где алгоритм может достигнуть соответствующей производительности и робастности с помощью контроллера более низкоуровневого, чем заданный с Временной интервал:
Если вы задаете |
|
Структура данных, содержащая информацию о производительности и робастности настроенного цикла ПИДа. Поля
Если |
Этот пример показывает, как разработать ПИД-регулятор для объекта, данного:
Как первая передача, создайте модель объекта и разработайте простой контроллер PI для него.
sys = zpk([],[-1 -1 -1],1);
[C_pi,info] = pidtune(sys,'PI')C_pi =
1
Kp + Ki * ---
s
with Kp = 1.14, Ki = 0.454
Continuous-time PI controller in parallel form.
info = struct with fields:
Stable: 1
CrossoverFrequency: 0.5205
PhaseMargin: 60.0000
C_pi является контроллером pid объект, который представляет контроллер PI. Поля info показывают, что настраивающийся алгоритм выбирает частоту перекрестного соединения разомкнутого цикла приблизительно 0,52 рад/с.
Исследуйте переходной процесс с обратной связью (отслеживание уставки) управляемой системы.
T_pi = feedback(C_pi*sys, 1); step(T_pi)

Чтобы улучшить время отклика, можно установить более высокую целевую перекрестную частоту, чем результат, который pidtune автоматически выбирает, 0.52. Увеличьте перекрестную частоту до 1,0.
[C_pi_fast,info] = pidtune(sys,'PI',1.0)C_pi_fast =
1
Kp + Ki * ---
s
with Kp = 2.83, Ki = 0.0495
Continuous-time PI controller in parallel form.
info = struct with fields:
Stable: 1
CrossoverFrequency: 1
PhaseMargin: 43.9973
Новый контроллер достигает более высокой перекрестной частоты, но за счет сокращенной прибыли фазы.
Сравните переходной процесс с обратной связью с этими двумя контроллерами.
T_pi_fast = feedback(C_pi_fast*sys,1); step(T_pi,T_pi_fast) axis([0 30 0 1.4]) legend('PI','PI,fast')

Это сокращение производительности заканчивается, потому что у контроллера PI нет достаточных степеней свободы, чтобы достигнуть хорошего поля фазы на перекрестной частоте 1,0 рад/с. Добавление производного действия улучшает ответ.
Разработайте контроллер PIDF для Gc с целевой перекрестной частотой 1,0 рад/с.
[C_pidf_fast,info] = pidtune(sys,'PIDF',1.0)C_pidf_fast =
1 s
Kp + Ki * --- + Kd * --------
s Tf*s+1
with Kp = 2.72, Ki = 0.985, Kd = 1.72, Tf = 0.00875
Continuous-time PIDF controller in parallel form.
info = struct with fields:
Stable: 1
CrossoverFrequency: 1
PhaseMargin: 60.0000
Поля информации показывают, что производное действие в контроллере позволяет настраивающемуся алгоритму разрабатывать более агрессивный контроллер, который достигает целевой перекрестной частоты с хорошим полем фазы.
Сравните переходной процесс с обратной связью и подавление помех для быстрого PI и контроллеров PIDF.
T_pidf_fast = feedback(C_pidf_fast*sys,1); step(T_pi_fast, T_pidf_fast); axis([0 30 0 1.4]); legend('PI,fast','PIDF,fast');

Можно сравнить вход (загрузка) подавление помех управляемой системы с быстрым PI и контроллерами PIDF. Для этого постройте ответ передаточной функции с обратной связью от входа объекта до объекта вывод.
S_pi_fast = feedback(sys,C_pi_fast); S_pidf_fast = feedback(sys,C_pidf_fast); step(S_pi_fast,S_pidf_fast); axis([0 50 0 0.4]); legend('PI,fast','PIDF,fast');

Этот график показывает, что контроллер PIDF также обеспечивает более быстрое подавление помех.
Разработайте ПИД-регулятор в стандартной форме для объекта, заданного
Чтобы разработать контроллер в стандартной форме, используйте контроллер стандартной формы в качестве аргумента C0 к pidtune.
sys = zpk([],[-1 -1 -1],1); C0 = pidstd(1,1,1); C = pidtune(sys,C0)
C =
1 1
Kp * (1 + ---- * --- + Td * s)
Ti s
with Kp = 2.18, Ti = 2.36, Td = 0.591
Continuous-time PID controller in standard form
Разработайте контроллер PI дискретного времени, использующий заданный метод, чтобы дискретизировать интегратор.
Если ваш объект находится в дискретное время, pidtune автоматически возвращает контроллер дискретного времени, использующий значение по умолчанию метод интегрирования Форварда Эйлера. Чтобы задать различный метод интегрирования, используйте pid или pidstd, чтобы создать контроллер дискретного времени, имеющий желаемый метод интегрирования.
sys = c2d(tf([1 1],[1 5 6]),0.1); C0 = pid(1,1,'Ts',0.1,'IFormula','BackwardEuler'); C = pidtune(sys,C0)
C =
Ts*z
Kp + Ki * ------
z-1
with Kp = -0.518, Ki = 10.4, Ts = 0.1
Sample time: 0.1 seconds
Discrete-time PI controller in parallel form.
Используя C0, когда вход заставляет pidtune разрабатывать контроллер C той же формы, вводить, и метод дискретизации как C0. Отображение показывает, что интегральный термин C использует Обратный Эйлеров метод интегрирования.
Задайте Трапециевидный интегратор и сравните получившийся контроллер.
C0_tr = pid(1,1,'Ts',0.1,'IFormula','Trapezoidal'); Ctr = pidtune(sys,C_tr)
Ctr =
Ts*(z+1)
Ki * --------
2*(z-1)
with Ki = 10.4, Ts = 0.1
Sample time: 0.1 seconds
Discrete-time I-only controller.Разработайте ПИД-регулятор 2-DOF для объекта, данного передаточной функцией:
Используйте целевую пропускную способность 1,5 рад/с.
wc = 1.5;
G = tf(1,[1 0.5 0.1]);
C2 = pidtune(G,'PID2',wc)C2 =
1
u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
s
with Kp = 1.26, Ki = 0.255, Kd = 1.38, b = 0.665, c = 0
Continuous-time 2-DOF PID controller in parallel form.
Используя тип 'PID2' заставляет pidtune генерировать контроллер 2-DOF, представленный как объект pid2. Отображение подтверждает этот результат. Отображение также показывает, что pidtune настраивает все коэффициенты контроллера, включая веса заданного значения b и c, чтобы сбалансировать производительность и робастность.
По умолчанию pidtune с входом type возвращает контроллер pid в параллельной форме. Чтобы разработать контроллер в стандартной форме, используйте контроллер pidstd в качестве входного параметра C0. Для получения дополнительной информации о параллельных и стандартных формах контроллера, смотрите страницы с описанием pidstd и pid.
Для получения информации о настраивающем алгоритме MathWorks® PID смотрите, что ПИД Настраивает Алгоритм.
Для интерактивной настройки ПИДа используйте PID Tuner. См. Проект ПИД-регулятора для Быстрого Отслеживания уставки для примера разработки контроллера, использующего PID Tuner.
PID Tuner не может разработать контроллеры для нескольких объектов целиком.
Åström, K. J. и Hägglund, T. Усовершенствованное управление ПИДом, Ресерч-Трайэнгел-Парк, NC: инструментирование, системы и общество автоматизации, 2006.