Exponenta Banner

pid2

Создайте ПИД-регулятор 2-DOF в параллельной форме, преобразуйте в параллельную форму ПИД-регулятор 2-DOF

свернуть все на странице

Контроллер pid2 объекты представляет две степени свободы (2-DOF) ПИД-регуляторы в параллельной форме. Используйте pid2 или чтобы создать контроллер pid2 объект из известных коэффициентов или преобразовать модель динамической системы в объект pid2.

Две степени свободы (2-DOF) ПИД-регуляторы включают взвешивание заданного значения на пропорциональных и производных условиях. ПИД-регулятор с 2 степенями свободы может достигнуть быстрого подавления помех без значительного увеличения перерегулирования в отслеживании заданного значения. ПИД-регуляторы 2-DOF также полезны, чтобы смягчить влияние изменений в ссылочном сигнале на управляющем сигнале. Следующий рисунок показывает типичную архитектуру управления с помощью ПИД-регулятора 2-DOF.

Синтаксис

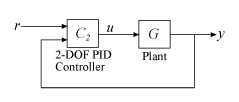
C2 = pid2(Kp,Ki,Kd,Tf,b,c)
C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts)
C2 = pid2(sys)
C2 = pid2(___,Name,Value)

Описание

C2 = pid2(Kp,Ki,Kd,Tf,b,c) создает непрерывно-разовый ПИД-регулятор 2-DOF с пропорциональным, интегралом, и производная получает Kp, Ki, и Kd и производная первого порядка фильтруют временную константу Tf. У контроллера также есть заданное значение, взвешивающее b на пропорциональном термине и заданное значение, взвешивающее c на производном термине. Отношение между контроллером 2-DOF вывело (u) и его два входных параметров (r, и y) дают:

u=Kp(br−y)+Kis(r−y)+KdsTfs+1(cr−y).

Это представление находится в parallel form. Если все коэффициенты с действительным знаком, то получившийся C2 является контроллером pid2 объект. Если один или несколько из этих коэффициентов является настраиваемым (realp или genmat), то C2 является настраиваемым обобщенным пространством состояний (genss) объект модели.

C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts) создает дискретное время ПИД-регулятор 2-DOF с шагом расчета Ts. Отношение между контроллером вывело, и входные параметры дают:

u=Kp(br−y)+KiIF(z)(r−y)+KdTf+DF(z)(cr−y).

IF (z) и DF (z) является discrete integrator formulas для интегратора и производного фильтра. По умолчанию,

IF(z)=DF(z)=Tsz−1.

Чтобы выбрать различные дискретные формулы интегратора, используйте свойства IFormula и DFormula. (См. Свойства для получения дополнительной информации). Если DFormula = 'ForwardEuler' (значение по умолчанию) и Tf ≠ 0, то Ts и Tf должны удовлетворить   Tf > Ts/2. Это требование гарантирует стабильный производный полюс фильтра.

C2 = pid2(sys) преобразовывает динамическую систему sys в параллельную форму контроллер pid2 объект.

C2 = pid2(___,Name,Value) задает дополнительные свойства как пары, разделенные запятой аргументов Name,Value.

Входные параметры

Kp

Пропорциональное усиление.

Kp может быть:

  • Действительное и конечное значение.

  • Массив действительных и конечных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для запланированной на усиление настройки, созданного использования tunableSurface.

Когда Kp = 0, у контроллера нет пропорционального действия.

Значение по умолчанию: 1

Ki

Интегральное усиление.

Ki может быть:

  • Действительное и конечное значение.

  • Массив действительных и конечных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для запланированной на усиление настройки, созданного использования tunableSurface.

Когда Ki = 0, у контроллера нет интегрального действия.

Значение по умолчанию: 0

Kd

Производное усиление.

Kd может быть:

  • Действительное и конечное значение.

  • Массив действительных и конечных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для запланированной на усиление настройки, созданного использования tunableSurface.

Когда Kd = 0, у контроллера нет производного действия.

Значение по умолчанию: 0

Tf

Временная константа производного фильтра первого порядка.

Tf может быть:

  • Действительное, конечное, и неотрицательное значение.

  • Массив действительных, конечных, и неотрицательных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для запланированной на усиление настройки, созданного использования tunableSurface.

Когда Tf = 0, у контроллера нет фильтра на производном действии.

Значение по умолчанию: 0

b

Взвешивание заданного значения на пропорциональном термине.

b может быть:

  • Действительное, неотрицательное, и конечное значение.

  • Массив действительных, неотрицательных, конечных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для запланированной на усиление настройки, созданного использования tunableSurface.

Когда b = 0, изменения в заданном значении не питаются непосредственно в пропорциональный термин.

Значение по умолчанию: 1

c

Взвешивание заданного значения на производном термине.

c может быть:

  • Действительное, неотрицательное, и конечное значение.

  • Массив действительных, неотрицательных, конечных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для запланированной на усиление настройки, созданного использования tunableSurface.

Когда c = 0, изменения в заданном значении не питаются непосредственно в производный термин.

Значение по умолчанию: 1

Ts

'SampleTime' .

Чтобы создать дискретное время контроллер pid2, обеспечьте положительное действительное значение (  Ts > 0). pid2 не поддерживает контроллеры дискретного времени с незаданным шагом расчета (  Ts = -1).

Ts должен быть скалярным значением. В массиве контроллеров pid2 у каждого контроллера должен быть тот же Ts.

Значение по умолчанию: 0 (непрерывное время)

sys

Динамическая система SISO, чтобы преобразовать, чтобы быть параллельными форме pid2.

sys должен быть 2D входом, системой с одним выходом. sys должен представлять допустимый ПИД-регулятор 2-DOF, который может быть написан в параллельной форме с Tf ≥ 0.

sys может также быть массивом динамических систем SISO.

Аргументы в виде пар имя-значение

Укажите необязательные аргументы в виде пар ""имя, значение"", разделенных запятыми. Имя (Name) — это имя аргумента, а значение (Value) — соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Используйте синтаксис Name,Value, чтобы установить формулы численного интегрирования IFormula и DFormula дискретного времени контроллер pid2, или установить другие свойства объектов, такие как InputName и OutputName. Для получения информации о доступных свойствах контроллера pid2 объекты смотрите Свойства.

Выходные аргументы

C2

ПИД-регулятор 2-DOF, возвращенный как контроллер pid2 объект, массив контроллера pid2 объекты, объект genss или массив genss.

  • Если все коэффициенты имеют скалярные числовые значения, то C2 является контроллером pid2 объект.

  • Если один или несколько коэффициентов являются числовым массивом, C2 является массивом контроллера pid2 объекты. Тип контроллера (такой как PI, ПИД или PDF) зависит от значений усилений. Например, когда Kd = 0, но Kp и Ki является ненулевым, C2 является контроллером PI.

  • Если один или несколько коэффициентов являются настраиваемым параметром (realp), обобщил матрицу (genmat) или настраиваемая поверхность усиления (tunableSurface), то C2 является обобщенной моделью в пространстве состояний (genss).

Свойства

b, c

Веса заданного значения на пропорциональных и производных условиях, соответственно. b и значения c действительны, конечны, и положительны. Когда вы используете команду pid2, чтобы создать ПИД-регулятор 2-DOF, b, и входные параметры c, соответственно, устанавливают начальные значения этих свойств.

Kp, Ki, Kd

Усиления ПИД-регулятора.

Пропорциональный, интеграл и производные усиления, соответственно. Kp, Ki и значения Kd действительны и конечны. Когда вы используете команду pid2, чтобы создать ПИД-регулятор 2-DOF, Kp, Ki, и входные параметры Kd, соответственно, устанавливают начальные значения этих свойств.

Tf

Производная временная константа фильтра.

Свойство Tf хранит производную временную константу фильтра контроллера pid2 объект. Tf действителен, конечен, и больше, чем или равен нулю. Когда вы создаете ПИД-регулятор 2-DOF с помощью команды pid2, входной параметр Tf устанавливает начальное значение этого свойства.

IFormula

Дискретная формула интегратора IF (z) для интегратора дискретного времени контроллер pid2 C2. Отношением между входными параметрами и выводом C2 дают:

u=Kp(br−y)+KiIF(z)(r−y)+KdTf+DF(z)(cr−y).

IFormula может принять следующие значения:

  • 'ForwardEuler' — IF (z) = Tsz−1.

    Эта формула является лучшей в течение времени небольшой выборки, где предел Найквиста является большим по сравнению с пропускной способностью контроллера. Для большего шага расчета формула ForwardEuler может привести к нестабильности, дискретизировав систему, которая стабильна в непрерывное время.

  • 'BackwardEuler' — IF (z) = Tszz−1.

    Преимущество формулы BackwardEuler состоит в том, что дискретизация стабильной непрерывно-разовой системы с помощью этой формулы всегда приводит к стабильному результату дискретного времени.

  • 'Trapezoidal' — IF (z) = Ts2z+1z−1.

    Преимущество формулы Trapezoidal состоит в том, что дискретизация стабильной непрерывно-разовой системы с помощью этой формулы всегда приводит к стабильному результату дискретного времени. Из всех доступных формул интегрирования формула Trapezoidal приводит к самому близкому соответствию между свойствами частотного диапазона дискретизированной системы и соответствующей непрерывно-разовой системы.

Когда C2 является непрерывно-кратным контроллером, IFormula является ''.

Значение по умолчанию: 'ForwardEuler'

DFormula

Дискретная формула интегратора DF (z) для производного фильтра дискретного времени контроллер pid2 C2. Отношением между входными параметрами и выводом C2 дают:

u=Kp(br−y)+KiIF(z)(r−y)+KdTf+DF(z)(cr−y).

DFormula может принять следующие значения:

  • 'ForwardEuler' — DF (z) = Tsz−1.

    Эта формула является лучшей в течение времени небольшой выборки, где предел Найквиста является большим по сравнению с пропускной способностью контроллера. Для большего шага расчета формула ForwardEuler может привести к нестабильности, дискретизировав систему, которая стабильна в непрерывное время.

  • 'BackwardEuler' — DF (z) = Tszz−1.

    Преимущество формулы BackwardEuler состоит в том, что дискретизация стабильной непрерывно-разовой системы с помощью этой формулы всегда приводит к стабильному результату дискретного времени.

  • 'Trapezoidal' — DF (z) = Ts2z+1z−1.

    Преимущество формулы Trapezoidal состоит в том, что дискретизация стабильной непрерывно-разовой системы с помощью этой формулы всегда приводит к стабильному результату дискретного времени. Из всех доступных формул интегрирования формула Trapezoidal приводит к самому близкому соответствию между свойствами частотного диапазона дискретизированной системы и соответствующей непрерывно-разовой системы.

    Значение Trapezoidal для DFormula не доступно контроллеру pid2 без производного фильтра (Tf = 0).

Когда C2 является непрерывно-кратным контроллером, DFormula является ''.

Значение по умолчанию: 'ForwardEuler'

InputDelay

Задержка в системе вводится. InputDelay всегда 0 для контроллера pid2 объект.

OutputDelay

Задержка в системе Вывод. OutputDelay всегда 0 для контроллера pid2 объект.

Ts

'SampleTime' . Для непрерывно-разовых моделей, Ts = 0. Для моделей дискретного времени Ts является положительной скалярной величиной, представляющей период выборки. Это значение выражается в модуле, заданном свойством TimeUnit модели. Модели ПИД-регулятора не поддерживают незаданный шаг расчета (Ts = -1).

Изменение этого свойства не дискретизирует или передискретизирует модель. Используйте c2d и d2c, чтобы преобразовать между непрерывным - и представлениями дискретного времени. Используйте d2d, чтобы изменить шаг расчета системы дискретного времени.

Значение по умолчанию: 0 (непрерывное время)

TimeUnit

Модули для переменной времени, шаг расчета Ts и любые задержки модели, заданной как одно из следующих значений:

  • 'nanoseconds'

  • 'microseconds'

  • 'milliseconds'

  • 'seconds'

  • 'minutes'

  • 'hours'

  • 'days'

  • 'weeks'

  • 'months'

  • 'years'

Изменение этого свойства не имеет никакого эффекта на другие свойства, и поэтому изменяет полное поведение системы. Используйте chgTimeUnit, чтобы преобразовать между единицами измерения времени, не изменяя поведение системы.

Значение по умолчанию: 'seconds'

InputName

Введите название канала, заданное как вектор символов или 2 1 массив ячеек из символьных векторов. Используйте это свойство назвать входные каналы моделей контроллеров. Например, присвойте имена setpoint и measurement к входным параметрам модели C ПИД-регулятора 2-DOF можно следующим образом.

C.InputName = {'setpoint';'measurement'};

Также используйте автоматическое векторное расширение, чтобы присвоить оба входных имени. Например:

C.InputName = 'C-input';

Входные имена автоматически расширяются до {'C-input(1)';'C-input(2)'}.

Можно использовать краткое обозначение u, чтобы относиться к свойству InputName. Например, C.u эквивалентен C.InputName.

Входные названия канала имеют несколько использования, включая:

  • Идентификация каналов на образцовом отображении и графиках

  • Определение точек контакта, когда взаимосвязанные модели

Значение по умолчанию: {'';''}

InputUnit

Введите модули канала, заданные как 2 1 массив ячеек из символьных векторов. Используйте это свойство отследить модули входного сигнала. Например, присвойте модули Volts ссылочному входу и модулям концентрации mol/m^3 к входу измерения модели C ПИД-регулятора 2-DOF можно следующим образом.

C.InputUnit = {'Volts';'mol/m^3'};

InputUnit не имеет никакого эффекта на поведение системы.

Значение по умолчанию: {'';''}

InputGroup

Введите группы канала. Это свойство не нужно для моделей ПИД-регулятора.

Значение по умолчанию: struct без полей

OutputName

Выведите название канала, заданное как вектор символов. Используйте это свойство назвать выходной канал моделей контроллеров. Например, присвойте имя control выводу моделей контроллеров C можно следующим образом.

C.OutputName = 'control';

Можно использовать краткое обозначение y, чтобы относиться к свойству OutputName. Например, C.y эквивалентен C.OutputName.

Входные названия канала имеют несколько использования, включая:

  • Идентификация каналов на образцовом отображении и графиках

  • Определение точек контакта, когда взаимосвязанные модели

Значение по умолчанию: Пустой символьный вектор, ''

OutputUnit

Выведите модули канала, заданные как вектор символов. Используйте это свойство отследить модули выходного сигнала. Например, присвойте модуль Volts выводу моделей контроллеров C можно следующим образом.

C.OutputUnit = 'Volts';

OutputUnit не имеет никакого эффекта на поведение системы.

Значение по умолчанию: Пустой символьный вектор, ''

OutputGroup

Выведите группы канала. Это свойство не нужно для моделей ПИД-регулятора.

Значение по умолчанию: struct без полей

Name

Имя системы, заданное как вектор символов. Например, 'system_1'.

Значение по умолчанию: ''

Notes

Любой текст, который вы хотите сопоставить с системой, сохраненной как строка или массив ячеек из символьных векторов. Свойство хранит, какой бы ни тип данных вы обеспечиваете. Например, если sys1 и sys2 являются моделями динамической системы, можно установить их свойства Notes можно следующим образом:

sys1.Notes = "sys1 has a string.";
sys2.Notes = 'sys2 has a character vector.';
sys1.Notes
sys2.Notes
ans = 

    "sys1 has a string."


ans =

    'sys2 has a character vector.'

Значение по умолчанию: [0×1 string]

UserData

Любой тип данных вы хотите сопоставить с системой, заданной как любой тип данных MATLAB®.

Значение по умолчанию: []

SamplingGrid

Выборка сетки для образцовых массивов, заданных как структура данных.

Для образцовых массивов, которые выведены путем выборки одной или нескольких независимых переменных, это дорожки свойства значения переменных, сопоставленные с каждой моделью в массиве. Эта информация появляется, когда вы отображаете или строите образцовый массив. Используйте эту информацию, чтобы проследить результаты до независимых переменных.

Установите имена полей структуры данных к именам переменных выборки. Установите значения полей к выбранным значениям переменных, сопоставленным с каждой моделью в массиве. Все переменные выборки должны быть числовыми и скаляр, оцененный, и все массивы выбранных значений должны совпадать с размерностями образцового массива.

Например, предположите, что вы создаете 11 1 массив линейных моделей, sysarr, путем взятия снимков состояния линейной изменяющейся во времени системы во времена t = 0:10. Следующий код хранит выборки времени линейными моделями.

 sysarr.SamplingGrid = struct('time',0:10)

Точно так же предположите, что вы создаете 6 9 образцовый массив, M, путем независимой выборки двух переменных, zeta и w. Следующий код присоединяет значения (zeta,w) к M.

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

Когда вы отображаете M, каждая запись в массиве включает соответствующий zeta и значения w. 

M
M(:,:,1,1) [zeta=0.3, w=5] =
 
        25
  --------------
  s^2 + 3 s + 25
 

M(:,:,2,1) [zeta=0.35, w=5] =
 
         25
  ----------------
  s^2 + 3.5 s + 25
 
...

Для образцовых массивов, сгенерированных путем линеаризации модели Simulink® в нескольких значениях параметров или рабочих точках, программное обеспечение заполняет SamplingGrid автоматически со значениями переменных, которые соответствуют каждой записи в массиве. Например, команды Simulink Control Design™ linearize и slLinearizer заполняют SamplingGrid таким образом.

Значение по умолчанию: []

Примеры

свернуть все

Скрипт Open Live Script

Создайте непрерывно-разовый контроллер 2-DOF с пропорциональными и производными усилениями и фильтр на производном термине. Для этого обнулите интегральное усиление. Установите другие усиления и временную константу фильтра к требуемым значениям.

Kp = 1;
Ki = 0;   % No integrator
Kd = 3;
Tf = 0.1;
b = 0.5;    % setpoint weight on proportional term
c = 0.5;    % setpoint weight on derivative term
C2 = pid2(Kp,Ki,Kd,Tf,b,c)
C2 =
 
                         s    
  u = Kp (b*r-y) + Kd -------- (c*r-y)
                       Tf*s+1 

  with Kp = 1, Kd = 3, Tf = 0.1, b = 0.5, c = 0.5
 
Continuous-time 2-DOF PDF controller in parallel form.

Отображение показывает тип контроллера, формулу и значения параметров, и проверяет, что у контроллера нет термина интегратора.

Скрипт Open Live Script

Создайте дискретное время контроллер PI 2-DOF, использующий трапециевидную формулу дискретизации. Задайте формулу с помощью синтаксиса Name,Value.

Kp = 5;
Ki = 2.4;
Kd = 0;    
Tf = 0; 
b = 0.5;   
c = 0;      
Ts = 0.1;
C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts,'IFormula','Trapezoidal')
C2 =
 
                      Ts*(z+1)
  u = Kp (b*r-y) + Ki -------- (r-y)
                      2*(z-1) 

  with Kp = 5, Ki = 2.4, b = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PI controller in parallel form.

Установка Kd = 0 задает контроллер PI без производного термина. Когда отображение показывает, значения Tf и c не используются в этом контроллере. Отображение также показывает, что трапециевидная формула используется для интегратора.

Скрипт Open Live Script

Создайте ПИД-регулятор 2-DOF и установите свойства InputName и OutputName динамической системы. Именование входных параметров и вывода полезно, например, когда вы соединяете ПИД-регулятор с другими моделями динамической системы с помощью команды connect.

C2 = pid2(1,2,3,0,1,1,'InputName',{'r','y'},'OutputName','u')
C2 =
 
                       1              
  u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
                       s              

  with Kp = 1, Ki = 2, Kd = 3, b = 1, c = 1
 
Continuous-time 2-DOF PID controller in parallel form.

ПИД-регулятор с 2 степенями свободы имеет два входных параметров и один вывод. Поэтому свойство 'InputName' является массивом, содержащим два имени, один для каждого входа. Образцовое отображение не показывает имена ввода и вывода для ПИД-регулятора, но можно исследовать значения свойств, чтобы видеть их. Например, проверьте входное имя контроллера.

C2.InputName
ans = 2x1 cell array
    {'r'}
    {'y'}
Скрипт Open Live Script

Создайте 2 3 сетка контроллеров PI 2-DOF с пропорциональным усилением в пределах от 1–2 через строки массивов и интегральное усиление в пределах от 5–9 через столбцы.

Чтобы создать массив ПИД-регуляторов, запустите с массивов, представляющих усиления. 

Kp = [1 1 1;2 2 2];
Ki = [5:2:9;5:2:9];

Когда вы передаете эти массивы команде pid2, команда возвращает массив контроллеров.

pi_array = pid2(Kp,Ki,0,0,0.5,0,'Ts',0.1,'IFormula','BackwardEuler');
size(pi_array)
2x3 array of 2-DOF PID controller.
Each PID has 1 output and 2 inputs.

Если вы предоставляете скалярные значения для некоторых коэффициентов, pid2 автоматически расширяет их и присваивает то же значение всем записям в массиве. Например, в этом примере, Kd = Tf = 0, так, чтобы все записи в массиве были контроллерами PI. Кроме того, все записи в массиве имеют b = 0.5.

Доступ к записям в массиве с помощью индексации массива. Для массивов динамической системы первые две размерности являются размерностями ввода-вывода модели, и остальные измерения являются измерениями массива. Поэтому следующая команда извлекает (2,3) запись в массиве.

pi23 = pi_array(:,:,2,3)
pi23 =
 
                       Ts*z 
  u = Kp (b*r-y) + Ki ------ (r-y)
                        z-1 

  with Kp = 2, Ki = 9, b = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PI controller in parallel form.

Можно также создать массив ПИД-регуляторов с помощью команды stack. 

C2 = pid2(1,5,0.1,0,0.5,0.5);         % PID controller
C2f = pid2(1,5,0.1,0.5,0.5,0.5);      % PID controller with filter
pid_array = stack(2,C2,C2f);          % stack along 2nd array dimension

Эти команды возвращаются 1 2 массив контроллеров.

size(pid_array)
1x2 array of 2-DOF PID controller.
Each PID has 1 output and 2 inputs.

Все ПИД-регуляторы в массиве должны иметь тот же шаг расчета, дискретные формулы интегратора и свойства динамической системы, такие как InputName и OutputName.

Скрипт Open Live Script

Преобразуйте стандартную форму контроллер pidstd2, чтобы быть параллельными форме.

Стандартная форма ПИДа выражает действия контроллера с точки зрения полного пропорционального усиления Kp, интегратор и производные временные константы Ti и Td и делитель фильтра N. Можно преобразовать любой контроллер стандартной формы 2-DOF, чтобы быть параллельными форме с помощью команды pid2. Например, рассмотрите следующий контроллер стандартной формы.

Kp = 2;
Ti = 3;
Td = 4;
N = 50;
b = 0.1;
c = 0.5;
C2_std = pidstd2(Kp,Ti,Td,N,b,c)
C2_std =
 
                       1      1                      s      
  u = Kp * [(b*r-y) + ---- * --- * (r-y) + Td * ------------ * (c*r-y)]
                       Ti     s                  (Td/N)*s+1 

  with Kp = 2, Ti = 3, Td = 4, N = 50, b = 0.1, c = 0.5
 
Continuous-time 2-DOF PIDF controller in standard form

Преобразуйте этот контроллер, чтобы быть параллельными форме с помощью pid2.

C2_par = pid2(C2_std)
C2_par =
 
                       1                s    
  u = Kp (b*r-y) + Ki --- (r-y) + Kd -------- (c*r-y)
                       s              Tf*s+1 

  with Kp = 2, Ki = 0.667, Kd = 8, Tf = 0.08, b = 0.1, c = 0.5
 
Continuous-time 2-DOF PIDF controller in parallel form.

График ответа подтверждает, что две формы эквивалентны.

bodeplot(C2_par,'b-',C2_std,'r--')
legend('Parallel','Standard','Location','Southeast')

Скрипт Open Live Script

Преобразуйте непрерывно-разовую динамическую систему, которая представляет ПИД-регулятор, чтобы быть параллельной форме pid.

Следующая динамическая система, с интегратором и двумя нулями, эквивалентна ПИД-регулятору.

H(s)=3(s+1)(s+2)s.

Создайте модель zpk H. Затем используйте команду pid, чтобы получить H с точки зрения коэффициентов ПИД Kp, Ki и Kd.

H = zpk([-1,-2],0,3);
C = pid(H)
C =
 
             1          
  Kp + Ki * --- + Kd * s
             s          

  with Kp = 9, Ki = 6, Kd = 3
 
Continuous-time PID controller in parallel form.
Скрипт Open Live Script

Преобразуйте динамическую систему дискретного времени, которая представляет ПИД-регулятор 2-DOF с производным фильтром, чтобы быть параллельной форме pid2.

Следующие матрицы пространства состояний представляют дискретное время ПИД-регулятор 2-DOF с шагом расчета 0,1 с.

A = [1,0;0,0.99];
B = [0.1,-0.1; -0.005,0.01];
C = [3,0.2];
D = [2.6,-5.2];
Ts = 0.1;
sys = ss(A,B,C,D,Ts);

Когда вы преобразовываете sys в форму ПИДа 2-DOF, результат зависит, на которых дискретных формулах интегратора вы задаете для преобразования. Например, используйте значение по умолчанию, ForwardEuler, и для интегратора и для производной.

C2fe = pid2(sys)
C2fe =
 
                        Ts                   1     
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ----------- (c*r-y)
                        z-1             Tf+Ts/(z-1)

  with Kp = 5, Ki = 3, Kd = 2, Tf = 10, b = 0.5, c = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

Теперь преобразуйте использование формулы Trapezoidal.

C2trap = pid2(sys,'IFormula','Trapezoidal','DFormula','Trapezoidal')
C2trap =
 
                      Ts*(z+1)                     1         
  u = Kp (b*r-y) + Ki -------- (r-y) + Kd ------------------- (c*r-y)
                      2*(z-1)             Tf+Ts/2*(z+1)/(z-1)

  with Kp = 4.85, Ki = 3, Kd = 2, Tf = 9.95, b = 0.485, c = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

Отображения показывают различие в получившихся содействующих значениях и функциональной форме.

Скрипт Open Live Script

Дискретизируйте непрерывно-разовый ПИД-регулятор 2-DOF и задайте интегральные и производные формулы фильтра.

Создайте непрерывно-кратный контроллер и дискретизируйте, это с помощью метода "нулевой порядок содержит" команды c2d.

C2con = pid2(10,5,3,0.5,1,1);  % continuous-time 2-DOF PIDF controller
C2dis1 = c2d(C2con,0.1,'zoh')
C2dis1 =
 
                        Ts                   1     
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ----------- (c*r-y)
                        z-1             Tf+Ts/(z-1)

  with Kp = 10, Ki = 5, Kd = 3.31, Tf = 0.552, b = 1, c = 1, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

Отображение показывает, что c2d вычисляет новые коэффициенты ПИДа для контроллера дискретного времени.

Дискретные формулы интегратора дискретизированного контроллера зависят от метода дискретизации c2d, как описано в Советах. Для метода zoh и IFormula и DFormula является ForwardEuler.

C2dis1.IFormula
ans = 
'ForwardEuler'

C2dis1.DFormula
ans = 
'ForwardEuler'

Если вы хотите использовать различные формулы от тех возвращенных c2d, то можно непосредственно установить Ts, IFormula и свойства DFormula контроллера к требуемым значениям.

C2dis2 = C2con;
C2dis2.Ts = 0.1; 
C2dis2.IFormula = 'BackwardEuler';
C2dis2.DFormula = 'BackwardEuler';

Однако эти команды не вычисляют новые коэффициенты ПИД для дискретизированного контроллера. Чтобы видеть это, исследуйте C2dis2 и сравните коэффициенты с C2con и C2dis1.

C2dis2
C2dis2 =
 
                       Ts*z                   1      
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ------------- (c*r-y)
                        z-1             Tf+Ts*z/(z-1)

  with Kp = 10, Ki = 5, Kd = 3, Tf = 0.5, b = 1, c = 1, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

Советы

  • Чтобы разработать ПИД-регулятор для конкретного объекта, используйте pidtune или pidTuner. Чтобы создать настраиваемый ПИД-регулятор 2-DOF как блок системы управления, используйте tunablePID2.

  • Повредить контроллер 2-DOF в два компонента элемента управления SISO, такие как контроллер обратной связи и feedforward контроллер, getComponents использования.

  • Создайте массивы контроллера pid2 объекты:

    • Задавая значения массивов для одного или нескольких коэффициентов Kp, Ki, Kd, Tf, b и c.

    • Определение массива динамических систем sys, чтобы преобразовать в контроллер pid2 объекты.

    • Используя stack, чтобы создать массивы из отдельных контроллеров или меньших массивов.

    • Передача массива моделей объекта управления к pidtune.

    В массиве контроллеров pid2 у каждого контроллера должен быть тот же шаг расчета Ts и дискретные формулы интегратора IFormula и DFormula.

  • Чтобы создать или преобразовать в контроллер стандартной формы, используйте pidstd2. Стандартная форма выражает действия контроллера с точки зрения полного пропорционального усиления Kp, интегральные и производные времена Ti и Td и делитель фильтра N. Например, отношением между входными параметрами и выводом непрерывно-разовой стандартной формы ПИД-регулятор 2-DOF дают:

    u=Kp[(br−y)+1Tis(r−y)+TdsTdNs+1(cr−y)].

  • Существует два способа дискретизировать непрерывно-кратный контроллер pid2:

    • Используйте команду c2d. c2d вычисляет новые значения параметров для дискретизированного контроллера. Дискретные формулы интегратора дискретизированного контроллера зависят от метода дискретизации c2d, который вы используете, как показано в следующей таблице.

      Метод дискретизации c2dIFormulaDFormula
      'zoh'ForwardEulerForwardEuler
      'foh'TrapezoidalTrapezoidal
      'tustin'TrapezoidalTrapezoidal
      'impulse'ForwardEulerForwardEuler
      'matched'ForwardEulerForwardEuler

      Для получения дополнительной информации о методах дискретизации c2d, Смотрите страницу с описанием c2d. Для получения дополнительной информации о IFormula и DFormula, смотрите Свойства.

    • Если вы требуете различных дискретных формул интегратора, можно дискретизировать контроллер непосредственно установкой Ts, IFormula и DFormula к требуемым значениям. (См., Дискретизируют Непрерывно-разовый ПИД-регулятор 2-DOF.) Однако этот метод не вычисляет новое усиление и постоянные значения фильтра для дискретизированного контроллера. Поэтому этот метод может привести к более плохому соответствию между непрерывным - и дискретным временем контроллеры pid2, чем использование c2d.

Смотрите также

| | | | | | | | |

Темы

Введенный в R2015b

Документация Control System Toolbox
Поддержка