Полиномиальными моделями для кривых дают
где n + 1 является порядком полинома, n является степенью полинома и 1 ≤ n ≤ 9. Порядок дает количество коэффициентов, чтобы быть подходящим, и степень дает самую высокую степень переменной прогноза.
В этом руководстве многочлены определены с точки зрения их степени. Например, (кубическим) полиномом третьей степени дают
Полиномы часто используются, когда простая эмпирическая модель требуется. Можно использовать полиномиальную модель для интерполяции или экстраполяции, или охарактеризовать данные с помощью глобальной подгонки. Например, преобразование температуры к напряжению для термопары Типа J в 0 к 760o диапазон температур описано полиномом седьмой степени.
Если вы не требуете глобальной параметрической подгонки и хотите максимизировать гибкость подгонки, кусочные полиномы могут обеспечить лучший подход. Обратитесь к Непараметрическому Подбору кривой для получения дополнительной информации.
Основные преимущества аппроксимаций полиномом включают разумную гибкость для данных, которые являются не слишком сложными, и они линейны, что означает, что подходящий процесс прост. Основной недостаток - то, что подгонки высокой степени могут стать нестабильными. Кроме того, полиномы любой степени могут обеспечить хорошую подгонку в области значений данных, но могут отличаться дико вне той области значений. Поэтому проявите осторожность при экстраполировании с полиномами.
Когда вы соответствуете полиномам высокой степени, подходящая процедура использует значения предиктора в качестве основания для матрицы с очень большими значениями, которые могут привести к масштабирующимся проблемам. Чтобы обработать это, необходимо нормировать данные путем центрирования его в нулевом среднем значении и масштабирования его к модульному стандартному отклонению. Нормируйте данные путем выбора Center и флажка шкалы в приложении Curve Fitting.
Откройте приложение Curve Fitting путем ввода cftool. Также нажмите Curve Fitting на вкладке Apps.
В приложении Curve Fitting выберите кривую или поверхностные данные.
Если вы выбираете данные о кривой (X data и Y data, или только Y data против индекса), приложение Curve Fitting создает подгонку кривой по умолчанию, Polynomial.
Если вы выбираете поверхностные данные (X data, Y data и Z data), приложение Curve Fitting создает поверхностную подгонку по умолчанию, Interpolant. Измените тип модели от Interpolant до Polynomial.
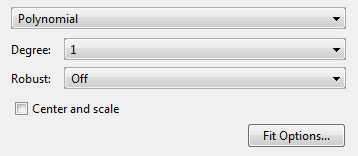
Для кривых модель Polynomial приспосабливает полином в x.
Для поверхностей модель Polynomial приспосабливает полином в x и y.
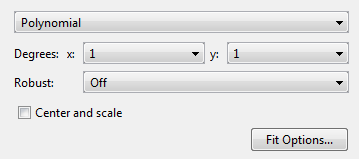
Можно задать следующие опции:
Степень для x и входных параметров y:
Для кривых степень x может быть до 9.
Для поверхностей степень x и y может быть до 5.
Степень полинома является максимумом x and y степени. См. Условия Полинома Определения для Полиномиальных Поверхностных Подгонок.
Устойчивый линейный метод наименьших квадратов подходящий метод, чтобы использовать (Off, LAR или Bisquare). Для получения дополнительной информации смотрите Robust на странице с описанием fitoptions.
Установите границы или исключите условия путем нажатия на Fit Options. Можно исключить любой термин путем установки его границ на 0.
Посмотрите в панели Results, чтобы видеть образцовые условия, значения коэффициентов и статистику качества подгонки.
Если ваши входные переменные имеют совсем другие шкалы, выберите и снимите флажок Center and scale, чтобы видеть различие в подгонке. Сообщения в панели Results предлагают вам, когда масштабирование может улучшить вашу подгонку.
Для примера, сравнивающего различные аппроксимации полиномом, смотрите, Выдерживают сравнение, Помещается в Приложение Curve Fitting.
Этот пример показывает, как использовать функцию fit, чтобы соответствовать полиномам к данным. Подгонка шагов и кривые полинома графика и поверхность, задайте подходящие опции, возвратите статистику качества подгонки, вычислите прогнозы и покажите доверительные интервалы.
Полиномиальная модель библиотеки является входным параметром к функциям fittype и подгонке. Задайте тип модели poly, сопровождаемый степенью в области x (до 9) или X и Y (до 5). Например, вы задаете квадратичную кривую с 'poly2' или кубическую поверхность с 'poly33'.
Создайте и постройте квадратичную полиномиальную кривую
Загрузите некоторые данные и соответствуйте квадратичному полиному. Задайте квадратичный, или полином второй степени со строкой 'poly2'.
load census; fitpoly2=fit(cdate,pop,'poly2') % Plot the fit with the plot method. plot(fitpoly2,cdate,pop) % Move the legend to the top left corner. legend('Location','NorthWest' );
fitpoly2 =
Linear model Poly2:
fitpoly2(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = 0.006541 (0.006124, 0.006958)
p2 = -23.51 (-25.09, -21.93)
p3 = 2.113e+04 (1.964e+04, 2.262e+04)

Создайте кубическую кривую
Соответствуйте кубическому полиному 'poly3'.
fitpoly3=fit(cdate,pop,'poly3')
plot(fitpoly3,cdate,pop)
Warning: Equation is badly conditioned. Remove repeated data points or try
centering and scaling.
fitpoly3 =
Linear model Poly3:
fitpoly3(x) = p1*x^3 + p2*x^2 + p3*x + p4
Coefficients (with 95% confidence bounds):
p1 = 3.855e-06 (-4.078e-06, 1.179e-05)
p2 = -0.01532 (-0.06031, 0.02967)
p3 = 17.78 (-67.2, 102.8)
p4 = -4852 (-5.834e+04, 4.863e+04)

Задайте подходящие опции
Кубическое соответствие предупреждает, что уравнение плохо обусловливается, таким образом, необходимо попытаться центрироваться и масштабироваться путем определения опции 'Normalize'. Соответствуйте кубическому полиному и центром и шкалой и устойчивыми подходящими опциями. Устойчивый 'on' является ярлыком, эквивалентным 'Bisquare', методу по умолчанию для устойчивого линейного метода наименьших квадратов подходящий метод.
fit3=fit(cdate, pop,'poly3','Normalize','on','Robust','on') plot(fit3,cdate,pop)
fit3 =
Linear model Poly3:
fit3(x) = p1*x^3 + p2*x^2 + p3*x + p4
where x is normalized by mean 1890 and std 62.05
Coefficients (with 95% confidence bounds):
p1 = -0.4619 (-1.895, 0.9707)
p2 = 25.01 (23.79, 26.22)
p3 = 77.03 (74.37, 79.7)
p4 = 62.81 (61.26, 64.37)

Чтобы узнать, какие параметры можно установить для модели 'poly3' библиотеки, используйте функцию fitoptions.
fitoptions poly3
ans =
Normalize: 'off'
Exclude: []
Weights: []
Method: 'LinearLeastSquares'
Robust: 'Off'
Lower: [1x0 double]
Upper: [1x0 double]
Получите статистику качества подгонки
Задайте выходной аргумент 'gof', чтобы получить статистику качества подгонки для подгонки кубического полинома.
[fit4, gof]=fit(cdate, pop,'poly3','Normalize','on'); gof
gof =
struct with fields:
sse: 149.7687
rsquare: 0.9988
dfe: 17
adjrsquare: 0.9986
rmse: 2.9682
Постройте невязки, чтобы оценить подгонку
Чтобы построить невязки, задайте 'residuals' как тип графика в методе графика.
plot(fit4,cdate, pop,'residuals');

Исследуйте подгонку вне области значений данных
По умолчанию подгонка построена в области значений данных. Чтобы построить подгонку в различной области значений, установите x-пределы осей прежде, чем построить подгонку. Например, чтобы видеть значения, экстраполируемые от подгонки, установите верхний x-предел 2 050.
plot( cdate, pop, 'o' ); xlim( [1900, 2050] ); hold on plot( fit4 ); hold off

Постройте границы прогноза
Чтобы построить границы прогноза, используйте 'predobs' или 'predfun' как тип графика.
plot(fit4,cdate,pop,'predobs')

Постройте границы прогноза для кубического полинома до года 2050.
plot( cdate, pop, 'o' ); xlim( [1900, 2050] ) hold on plot( fit4, 'predobs' ); hold off

Получите доверительные границы в новых точках запроса
Оцените пригодное для некоторых новых точек запроса.
cdateFuture = (2000:10:2020).'; popFuture = fit4( cdateFuture )
popFuture = 276.9632 305.4420 335.5066
Вычислите 95% доверительных границ на прогнозе для генеральной совокупности в будущем, с помощью метода перед вмятиной.
ci = predint( fit4, cdateFuture, 0.95, 'observation' )
ci = 267.8589 286.0674 294.3070 316.5770 321.5924 349.4208
Постройте предсказанную будущую генеральную совокупность, с доверительными интервалами, против подгонки и данных.
plot(cdate, pop, 'o'); xlim([1900, 2040]) hold on plot(fit4) h = errorbar(cdateFuture,popFuture,popFuture-ci(:,1),ci(:,2)-popFuture,'.'); hold off legend('cdate v pop','poly3','prediction','Location','NorthWest')

Соответствуйте и постройте полиномиальную поверхность
Загрузите некоторые поверхностные данные и приспособьте полином четвертой степени в X и Y.
load franke; fitsurface=fit([x,y],z, 'poly44','Normalize','on') plot(fitsurface, [x,y],z)
Linear model Poly44:
fitsurface(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p30*x^3
+ p21*x^2*y + p12*x*y^2 + p03*y^3 + p40*x^4 + p31*x^3*y
+ p22*x^2*y^2 + p13*x*y^3 + p04*y^4
where x is normalized by mean 1982 and std 868.6
and where y is normalized by mean 0.4972 and std 0.2897
Coefficients (with 95% confidence bounds):
p00 = 0.3471 (0.3033, 0.3909)
p10 = -0.1502 (-0.1935, -0.107)
p01 = -0.4203 (-0.4637, -0.377)
p20 = 0.2165 (0.1514, 0.2815)
p11 = 0.1717 (0.1175, 0.2259)
p02 = 0.03189 (-0.03351, 0.09729)
p30 = 0.02778 (0.00749, 0.04806)
p21 = 0.01501 (-0.002807, 0.03283)
p12 = -0.03659 (-0.05439, -0.01879)
p03 = 0.1184 (0.09812, 0.1387)
p40 = -0.07661 (-0.09984, -0.05338)
p31 = -0.02487 (-0.04512, -0.004624)
p22 = 0.0007464 (-0.01948, 0.02098)
p13 = -0.02962 (-0.04987, -0.009366)
p04 = -0.02399 (-0.0474, -0.0005797)

Все подходящие методы имеют значение по умолчанию properties Normalize, Exclude, Weights и Method. Для примера см. Опции Подгонки Определения в Командной строке.
Полиномиальные модели имеют значение свойства Method LinearLeastSquares и дополнительные подходящие свойства опций, показанные в следующей таблице. Для получения дополнительной информации на всех подходящих опциях, смотрите страницу с описанием fitoptions.
Свойство | Описание |
|---|---|
| Задает устойчивый линейный метод наименьших квадратов подходящий метод, чтобы использовать. Значениями является |
| Вектор нижних границ на коэффициентах, которые будут адаптированы. Значение по умолчанию является пустым вектором, указывая, что подгонка неограничена нижними границами. Если границы заданы, длина вектора должна равняться количеству коэффициентов. Отдельные неограниченные нижние границы могут быть заданы |
| Вектор верхних границ на коэффициентах, которые будут адаптированы. Значение по умолчанию является пустым вектором, указывая, что подгонка неограничена верхними границами. Если границы заданы, длина вектора должна равняться количеству коэффициентов. Отдельные неограниченные верхние границы могут быть заданы |
Можно управлять условиями, чтобы включать в полиномиальную поверхностную модель путем определения степеней для входных параметров X и Y. Если i является степенью в области x, и j является степенью в области y, общая степень полинома является максимумом i и j. Степень x в каждом термине меньше чем или равна i, и степень y в каждом термине меньше чем или равна j. Максимум и для i и для j равняется пяти.
Например:
poly21 Z = p00 + p10*x + p01*y + p20*x^2 + p11*x*y
poly13 Z = p00 + p10*x + p01*y + p11*x*y + p02*y^2
+ p12*x*y^2 + p03*y^3poly55 Z = p00 + p10*x + p01*y +...+ p14*x*y^4
+ p05*y^5Например, если вы задаете x степень 3 и y степень 2, именем модели является poly32. Образцовые условия следуют за формой в этой таблице.
| Степень термина | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 1 | y | y2 |
| 1 | x | x, y | xy2 |
| 2 | x2 | x2y | Нет данных |
| 3 | x3 | Нет данных | Нет данных |
Общая степень полинома не может превысить максимум i и j. В этом примере исключены условия, такие как x3y и x2y2, потому что их степени суммируют к больше, чем 3. В обоих случаях общей степенью является 4.
Полиномиальные имена модели и уравнения | fit | fitoptions | fittype