Эти примеры показывают, как оценить последовательную корреляцию при помощи приложения Econometric Modeler. Методы включают графический вывод автокорреляционной функции (ACF) и частичная автокорреляционная функция (PACF) и тестирование на значительные коэффициенты задержки с помощью Q-теста Ljung-поля. Набор данных, который хранится в mlr/examples/econ/Data_Overshort.mat, содержит 57 дней подряд сверхкоротких замыканий от бензобака в Колорадо. Папка mlr является значением matlabroot.
Этот пример показывает, как построить ACF и PACF временных рядов.
В командной строке загрузите набор данных Data_Overshort.mat.
load(fullfile(matlabroot,'examples','econ','Data_Overshort.mat'))
В командной строке откройте приложение Econometric Modeler.
econometricModeler
Также откройте приложение из галереи приложений (см. Econometric Modeler).
Импортируйте DataTable в приложение:
На вкладке Econometric Modeler, в разделе Import, нажатии кнопки![]() .
.
В диалоговом окне Import Data, в столбце Import?, устанавливают флажок для переменной DataTable.
Нажмите Import.
Переменная OSHORT появляется в Data Browser, и его график временных рядов появляется в окне рисунка Time Series Plot(OSHORT).
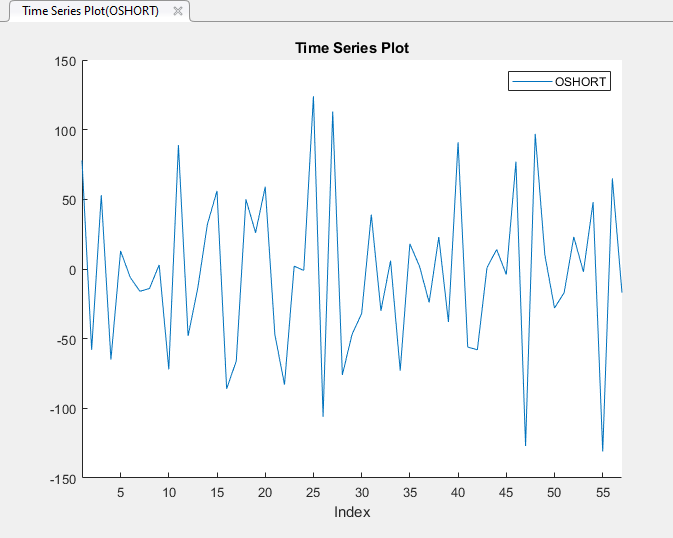
Ряд, кажется, является стационарным.
Закройте окно рисунка Time Series Plot(OSHORT).
Постройте ACF OSHORT путем нажатия на вкладку Plots. ACF появляется в окне рисунка ACF(OSHORT), затем нажатии по ACF.
Постройте PACF OSHORT путем нажатия на вкладку Plots, затем нажатие по PACF. PACF появляется в окне рисунка PACF(OSHORT).
Расположите коррелограммы так, чтобы можно было просмотреть их одновременно путем перетаскивания окна рисунка PACF(OSHORT) к нижней части правой панели.
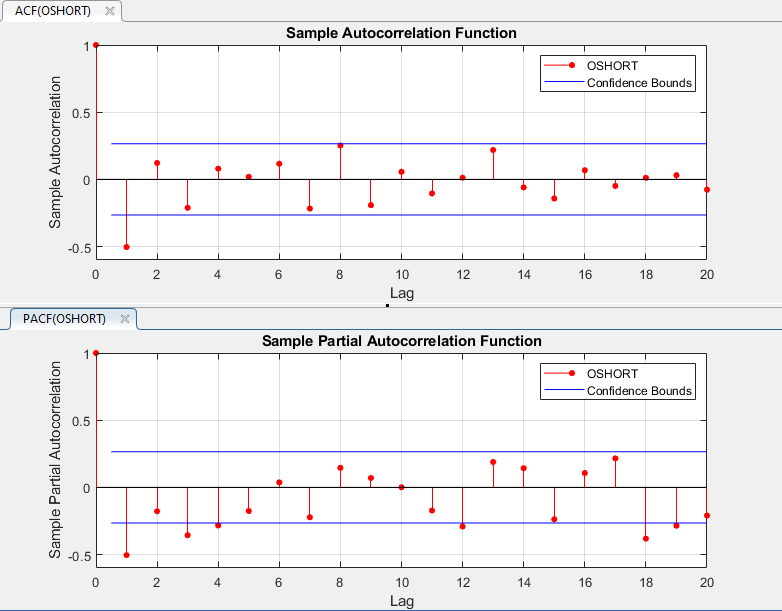
Демонстрационный ACF и PACF показывают значительную автокорреляцию (то есть, оба содержат задержки, которые являются больше чем двумя стандартными отклонениями далеко от 0). Демонстрационный ACF показывает, что автокорреляция в задержке 1 является значительной. Демонстрационный PACF показывает, что автокорреляции в задержках 1, 3, и 4 являются значительными.
Отличное сокращение ACF и более постепенное затухание PACF предполагают, что модель MA (1) может подходить для этих данных.
Этот пример показывает, как провести Q-тест Ljung-поля для значительных задержек автокорреляции.
В командной строке загрузите набор данных Data_Overshort.mat.
load(fullfile(matlabroot,'examples','econ','Data_Overshort.mat'))
В командной строке откройте приложение Econometric Modeler.
econometricModeler
Также откройте приложение из галереи приложений (см. Econometric Modeler).
Импортируйте DataTable в приложение:
На вкладке Econometric Modeler, в разделе Import, нажатии кнопки![]() .
.
В диалоговом окне Import Data, в столбце Import?, устанавливают флажок для переменной DataTable.
Нажмите Import.
Переменная OSHORT появляется в Data Browser, и его график временных рядов появляется в окне рисунка Time Series Plot(OSHORT).

Ряд, кажется, является стационарным, и он колеблется вокруг постоянного среднего значения. Поэтому вы не должны преобразовывать данные прежде, чем провести тест.
Проведите три Q-теста Ljung-поля для тестирования нулевой гипотезы, что первые 10, 5, и 1 автокорреляция являются совместно нулевыми:
На вкладке Econometric Modeler, в разделе Tests, нажимают New Test> Ljung-Box Q-Test.
На вкладке LBQ, в разделе Parameters:
Установите Number of Lags на 10.
Установите DOF на 10.
Чтобы достигнуть ложного положительного уровня ниже 0.05, используйте исправление Bonferroni для set Significance Level к 0.05/3 = 0.0167.
В разделе Tests нажмите Run Test.
Повторите шаги 2 и 3 дважды с этими изменениями:
Установите Number of Lags на 5 и DOF к 5.
Установите Number of Lags на 1 и DOF к 1.
Результаты испытаний появляются в таблице Results документа LBQ(OSHORT).
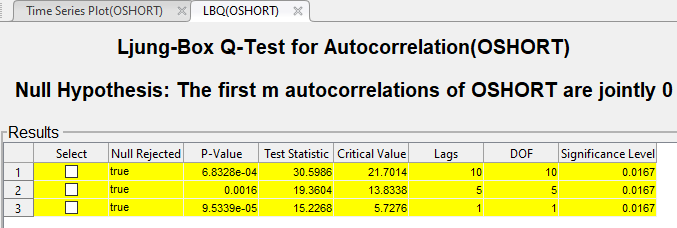
Результаты показывают, что не каждая автокорреляция, чтобы отстать 5 (или 10) является нулем, указывая на энергозависимость, кластеризирующуюся в остаточном ряду.