Чтобы создать полностью заданную задачу оптимизации портфеля среднего отклонения, инстанцируйте объекта Portfolio с помощью Portfolio. Для получения информации о рабочем процессе при использовании объектов Портфеля смотрите Рабочий процесс Объекта Портфеля.
Используйте Portfolio, чтобы создать экземпляр объекта класса Portfolio. Можно использовать Portfolio несколькими способами. Чтобы настроить задачу оптимизации портфеля в объекте Portfolio, самый простой синтаксис:
p = Portfolio;
p, такой, что все свойства объектов пусты. Объект Portfolio также принимает наборы аргументов пары "имя-значение" аргумента для свойств и их значений. Объект Portfolio принимает входные параметры для публичных свойств с общим синтаксисом:
p = Portfolio('property1', value1, 'property2', value2, ... );Если объект Portfolio уже существует, синтаксис разрешает первому (и только первый аргумент) Portfolio быть существующим объектом с последующими аргументами пары "имя-значение" аргумента для свойств, которые будут добавлены или изменены. Например, учитывая существующий объект Portfolio в p, общий синтаксис:
p = Portfolio(p, 'property1', value1, 'property2', value2, ... );
Имена входного параметра не являются чувствительными к регистру, но должны быть полностью заданы. Кроме того, несколько свойств могут быть заданы с альтернативными именами аргумента (см. Ярлыки для Имен свойства). Объект Portfolio обнаруживает проблемные размерности от входных параметров и, когда-то набор, последующие входные параметры могут подвергнуться различным скалярным или матричным операциям расширения, которые упрощают полный процесс, чтобы сформулировать проблему. Кроме того, объект Portfolio является объектом значения так, чтобы, учитывая портфель p следующий код создал два объекта, p и q, которые отличны:
q = Portfolio(p, ...)
Оптимизация портфеля среднего отклонения полностью задана с объектом Portfolio, если эти два условия соблюдают:
Моменты возвратов актива должны быть заданы таким образом, что свойство AssetMean содержит допустимый конечный средний вектор актива, возвращается, и свойство AssetCovar содержит допустимую симметричную положительно-полуопределенную матрицу для ковариации актива, возвращается.
Первое условие удовлетворено путем установки свойств, сопоставленных с моментами актива, возвращается.
Набор выполнимых портфелей должен быть непустым компактным набором, где компактный набор закрыт и ограничен.
Второе условие удовлетворено обширным набором свойств, которые задают различные типы ограничений, чтобы сформировать набор выполнимых портфелей. Поскольку такие наборы должны быть ограничены, или явные или неявные ограничения могут быть наложены, и несколько функций, таких как estimateBounds, обеспечить способы гарантировать, что ваша проблема правильно формулируется.
Несмотря на то, что общие условия достаточности для оптимизации портфеля среднего отклонения идут вне этих двух условий, объект Portfolio, реализованный в Financial Toolbox™ неявно, обрабатывает все эти дополнительные условия. Для получения дополнительной информации о модели Markowitz для оптимизации портфеля среднего отклонения смотрите Оптимизацию Портфеля.
Если вы создаете объект Portfolio, p, без входных параметров, можно отобразить его с помощью disp:
p = Portfolio; disp(p); Portfolio
Portfolio with properties:
BuyCost: []
SellCost: []
RiskFreeRate: []
AssetMean: []
AssetCovar: []
TrackingError: []
TrackingPort: []
Turnover: []
BuyTurnover: []
SellTurnover: []
Name: []
NumAssets: []
AssetList: []
InitPort: []
AInequality: []
bInequality: []
AEquality: []
bEquality: []
LowerBound: []
UpperBound: []
LowerBudget: []
UpperBudget: []
GroupMatrix: []
LowerGroup: []
UpperGroup: []
GroupA: []
GroupB: []
LowerRatio: []
UpperRatio: []
BoundType: []
MinNumAssets: []
MaxNumAssets: []
Перечисленные подходы обеспечивают способ настроить задачу оптимизации портфеля с объектом Portfolio. Функции set предлагают дополнительные способы установить и изменить наборы свойств в объекте Portfolio.
Можно использовать объект Portfolio непосредственно настроить “стандартную” задачу оптимизации портфеля, учитывая среднее значение, и ковариация актива возвращается в переменных m и C:
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio('assetmean', m, 'assetcovar', C, ...
'lowerbudget', 1, 'upperbudget', 1, 'lowerbound', 0);LowerBound подвергается скалярному расширению, поскольку AssetMean и AssetCovar обеспечивают размерности проблемы.Можно использовать запись через точку с функциональным plotFrontier.
p.plotFrontier;
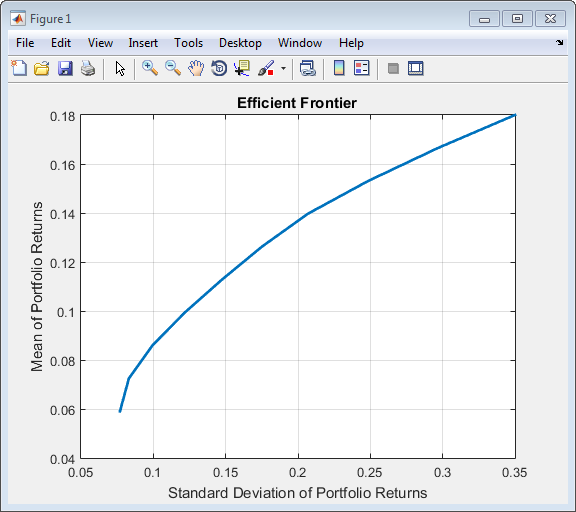
Альтернативный способ выполнить ту же задачу подготовки “стандартной” задачи оптимизации портфеля, учитывая среднее значение и ковариацию актива возвращается в переменных m и C (который также иллюстрирует, что имена аргумента не являются чувствительными к регистру):
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio;
p = Portfolio(p, 'assetmean', m, 'assetcovar', C);
p = Portfolio(p, 'lowerbudget', 1, 'upperbudget', 1);
p = Portfolio(p, 'lowerbound', 0);
plotFrontier(p);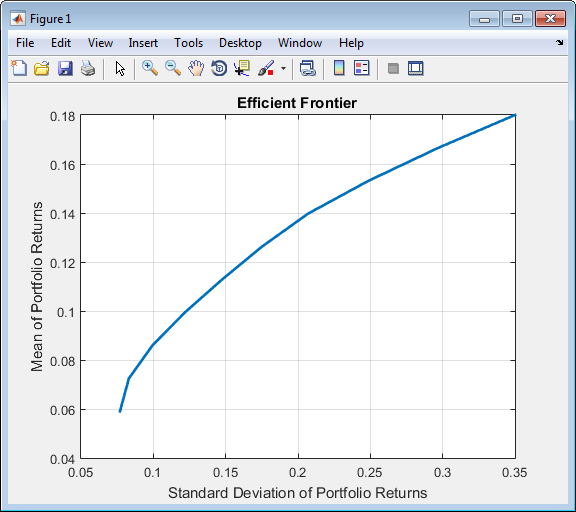
Этот путь работает, потому что вызовы Portfolio находятся в этом конкретном порядке. В этом случае вызов, чтобы инициализировать AssetMean и AssetCovar обеспечивает размерности для проблемы. Если бы необходимо было выполнить этот шаг в последний раз, необходимо было бы явным образом определить размеры свойства LowerBound можно следующим образом:
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio;
p = Portfolio(p, 'LowerBound', zeros(size(m)));
p = Portfolio(p, 'LowerBudget', 1, 'UpperBudget', 1);
p = Portfolio(p, 'AssetMean', m, 'AssetCovar', C);
plotFrontier(p);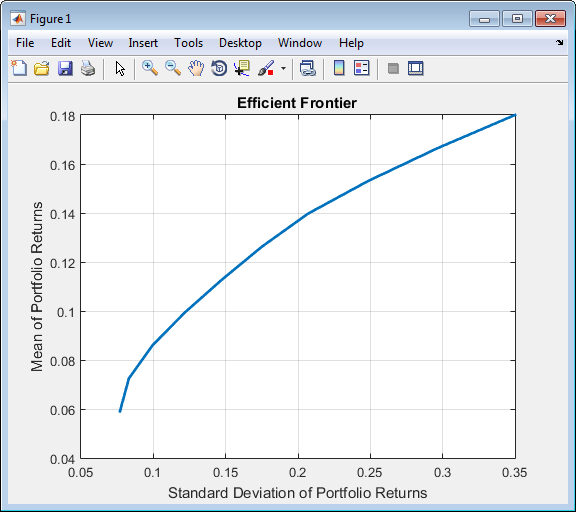
Если вы не задавали размер LowerBound, но, вместо этого, вводили скалярный аргумент, объект Portfolio принимает, что вы задаете проблему одно актива, и производит ошибку в вызове, чтобы установить моменты актива с четырьмя активами.
Объект Portfolio имеет более короткие имена аргумента, которые заменяют более длинные имена аргумента, сопоставленные на определенные свойства объекта Portfolio. Например, вместо того, чтобы ввести 'assetcovar', объект Portfolio принимает, что нечувствительное к регистру имя 'covar' устанавливает свойство AssetCovar в объекте Portfolio. Каждое более короткое имя аргумента соответствует одному свойству в объекте Portfolio. Одним исключением является альтернативное имя аргумента 'budget', который показывает обоих свойства LowerBudget и UpperBudget. Когда 'budget' используется, затем свойства LowerBudget и UpperBudget собираются в то же значение сформировать ограничение бюджета равенства.
Ярлыки для имен свойства
Имя аргумента ярлыка | Эквивалентный Аргумент / Имя свойства |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например, этот вызов Portfolio использует эти ярлыки для свойств и эквивалентен предыдущим примерам:
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio('mean', m, 'covar', C, 'budget', 1, 'lb', 0);
plotFrontier(p);
Несмотря на то, что не рекомендуемый, можно установить свойства непосредственно, однако никакая проверка ошибок не сделана на входных параметрах:
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio;
p.NumAssets = numel(m);
p.AssetMean = m;
p.AssetCovar = C;
p.LowerBudget = 1;
p.UpperBudget = 1;
p.LowerBound = zeros(size(m));
plotFrontier(p);