Этот пример показывает, как использовать два различных метода, чтобы калибровать стохастическую модель энергозависимости SABR от подразумеваемых Черных колебаний рынка. Оба подхода используют blackvolbysabr.
Загрузите рынок подразумеваемые черные данные об энергозависимости
Метод 2: калибруйте ро и ню допущением альфы от энергозависимости в деньгах
Этот пример показывает, как настроить подразумеваемые Черные колебания гипотетического рынка для европейского swaptions в области значений забастовок перед калибровкой. swaptions истекают за три года с даты Settle и имеют 10-летние подкачки как базовый инструмент. Уровни выражаются в десятичных числах. (Изменение модулей влияет на численное значение и интерпретацию параметра входа Alpha к функциональному blackvolbysabr.)
Загрузите подразумеваемые Черные данные об энергозависимости рынка для swaptions, истекающего за три года.
Settle = '12-Jun-2013'; ExerciseDate = '12-Jun-2016'; MarketStrikes = [2.0 2.5 3.0 3.5 4.0 4.5 5.0]'/100; MarketVolatilities = [45.6 41.6 37.9 36.6 37.8 39.2 40.0]'/100;
Во время Settle задайте базовый форвардный курс и энергозависимость в деньгах.
CurrentForwardValue = MarketStrikes(4) ATMVolatility = MarketVolatilities(4)
CurrentForwardValue =
0.0350
ATMVolatility =
0.3660Этот пример показывает, как калибровать the Alpha, Rho и параметры входа Nu непосредственно. Значение Beta предопределяется или путем подбора кривой историческим данным о волатильности рынка или путем выбора значения, которое считают подходящим для того рынка [1].
Задайте предопределенный Beta.
Beta1 = 0.5;
После фиксации значения (Beta), параметры \alpha, (Rho), и (Nu) все адаптирован непосредственно. lsqnonlin функции Optimization Toolbox™ генерирует значения параметров, которые минимизируют квадратичную невязку между волатильностью рынка и колебаниями, вычисленными blackvolbysabr.
% Calibrate Alpha, Rho, and Nu objFun = @(X) MarketVolatilities - ... blackvolbysabr(X(1), Beta1, X(2), X(3), Settle, ... ExerciseDate, CurrentForwardValue, MarketStrikes); X = lsqnonlin(objFun, [0.5 0 0.5], [0 -1 0], [Inf 1 Inf]); Alpha1 = X(1); Rho1 = X(2); Nu1 = X(3);
Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the default value of the function tolerance.
Этот пример показывает, как использовать альтернативный калибровочный метод где значение (Beta) снова предопределяется как в Методе 1.
Задайте предопределенный Beta.
Beta2 = 0.5;
Однако после фиксации значения (Beta), параметры (Rho), и (Nu) адаптирован непосредственно в то время как (Alpha) подразумевается с рынка энергозависимость в деньгах. Калиброванное использование моделей этого метода производит колебания в деньгах, которые равны рыночным котировкам. Этот подход широко используется в swaptions, где колебания в деньгах заключаются в кавычки наиболее часто и важны для соответствия. Подразумевать (Alpha) с рынка энергозависимость в деньгах (), следующий кубический полином решен для (Alpha) и самый маленький положительный действительный корень выбраны [2].
где:
текущее прямое значение.
часть года к зрелости.
Чтобы выполнить это, задайте анонимную функцию как:
% Year fraction from Settle to option maturity T = yearfrac(Settle, ExerciseDate, 1); % This function solves the SABR at-the-money volatility equation as a % polynomial of Alpha alpharoots = @(Rho,Nu) roots([... (1 - Beta2)^2*T/24/CurrentForwardValue^(2 - 2*Beta2) ... Rho*Beta2*Nu*T/4/CurrentForwardValue^(1 - Beta2) ... (1 + (2 - 3*Rho^2)*Nu^2*T/24) ... -ATMVolatility*CurrentForwardValue^(1 - Beta2)]); % This function converts at-the-money volatility into Alpha by picking the % smallest positive real root atmVol2SabrAlpha = @(Rho,Nu) min(real(arrayfun(@(x) ... x*(x>0) + realmax*(x<0 || abs(imag(x))>1e-6), alpharoots(Rho,Nu))));
Функциональный atmVol2SabrAlpha преобразовывает энергозависимость в деньгах в (Alpha) для данного набора (Rho) и \nu. Эта функция затем используется в целевой функции, чтобы соответствовать параметрам (Rho) и \nu.
% Calibrate Rho and Nu (while converting at-the-money volatility into Alpha % using atmVol2SabrAlpha) objFun = @(X) MarketVolatilities - ... blackvolbysabr(atmVol2SabrAlpha(X(1), X(2)), ... Beta2, X(1), X(2), Settle, ExerciseDate, CurrentForwardValue, ... MarketStrikes); X = lsqnonlin(objFun, [0 0.5], [-1 0], [1 Inf]); Rho2 = X(1); Nu2 = X(2);
Local minimum found. Optimization completed because the size of the gradient is less than the default value of the function tolerance.
Калиброванный параметр (Alpha) вычисляется с помощью калиброванных параметров (Rho) и \nu.
% Obtain final Alpha from at-the-money volatility using calibrated parameters Alpha2 = atmVol2SabrAlpha(Rho2, Nu2); % Display calibrated parameters C = {Alpha1 Beta1 Rho1 Nu1;Alpha2 Beta2 Rho2 Nu2}; CalibratedPrameters = cell2table(C,... 'VariableNames',{'Alpha' 'Beta' 'Rho' 'Nu'},... 'RowNames',{'Method 1';'Method 2'})
CalibratedPrameters =
Alpha Beta Rho Nu
________ ____ _______ _______
Method 1 0.060277 0.5 0.2097 0.75091
Method 2 0.058484 0.5 0.20568 0.79647
Этот пример показывает, как использовать калиброванные модели, чтобы вычислить новые колебания в любом значении забастовки.
Вычислите колебания для моделей, калиброванных с помощью Метода 1 и Метода 2, и постройте результаты.
PlottingStrikes = (1.75:0.1:5.50)'/100; % Compute volatilities for model calibrated by Method 1 ComputedVols1 = blackvolbysabr(Alpha1, Beta1, Rho1, Nu1, Settle, ... ExerciseDate, CurrentForwardValue, PlottingStrikes); % Compute volatilities for model calibrated by Method 2 ComputedVols2 = blackvolbysabr(Alpha2, Beta2, Rho2, Nu2, Settle, ... ExerciseDate, CurrentForwardValue, PlottingStrikes); figure; plot(MarketStrikes,MarketVolatilities,'xk',... PlottingStrikes,ComputedVols1,'b', ... PlottingStrikes,ComputedVols2,'r', ... CurrentForwardValue,ATMVolatility,'ok',... 'MarkerSize',10); xlim([0.01 0.06]); ylim([0.35 0.5]); xlabel('Strike', 'FontWeight', 'bold'); ylabel('Implied Black Volatility', 'FontWeight', 'bold'); legend('Market Volatilities', 'SABR Model (Method 1)',... 'SABR Model (Method 2)', 'At-the-money volatility');
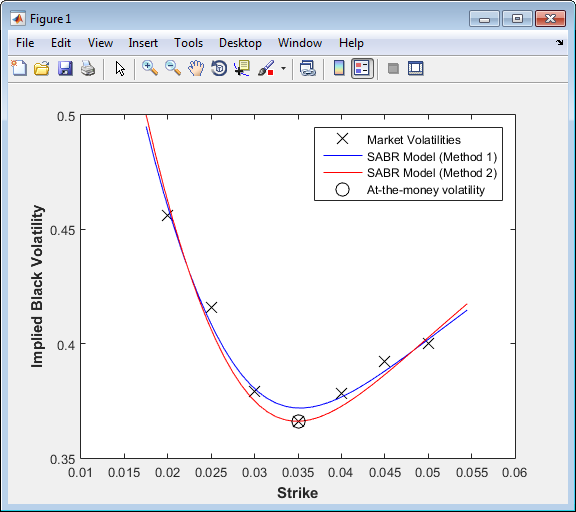
Модель, калиброванная с помощью Метода 2, воспроизводит рынок энергозависимость в деньгах (отмеченный кругом) точно.
[1] Хейган, P. S. Кумар, D., Лесниевский, A. S. и Лесничий, Д. Э., Управляя риском улыбки, Журналом Wilmott, 2002.
[2] Запад, G., “Калибровка Модели SABR на Неликвидных Рынках”, Прикладные Математические Финансы, 12 (4), стр 371–385, 2004.
blackvolbysabr | optsensbysabr | swaptionbyblk