Этот пример показывает, как минимизировать функцию Рэстриджина с шестью решателями. Каждый решатель имеет свои собственные характеристики. Характеристики приводят к различным решениям и время выполнения. Результаты, исследованные в, Сравнивают Синтаксис и Решения, может помочь вам выбрать соответствующий решатель для своих собственных проблем.
Функция Рэстриджина имеет много локальных минимумов с глобальным минимумом в (0,0):
Обычно вы не знаете местоположение глобального минимума вашей целевой функции. Чтобы показать, как решатели ищут глобальное решение, этот пример запускает все решатели вокруг точки [20,30], который далек от глобального минимума.
Файл rastriginsfcn.m реализует функцию Рэстриджина. Этот файл идет с программным обеспечением Global Optimization Toolbox. Этот пример использует масштабированную версию функции Рэстриджина с большими бассейнами привлекательности. Для получения информации смотрите Бассейны Привлекательности.
rf2 = @(x)rastriginsfcn(x/10);
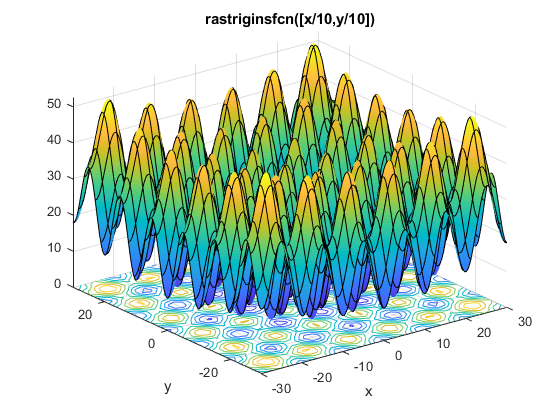
Этот пример минимизирует rf2 с помощью настроек по умолчанию fminunc (решатель Optimization Toolbox™), patternsearch и GlobalSearch. Пример также использует ga и particleswarm с опциями не по умолчанию, чтобы запустить с начальной генеральной совокупности вокруг точки [20,30]. Поскольку surrogateopt требует конечных границ, пример использует surrogateopt с нижними границами -70 и верхними границами 130 в каждой переменной.
Решить задачу оптимизации с помощью решателя Optimization Toolbox fminunc, введите:
rf2 = @(x)rastriginsfcn(x/10); % objective x0 = [20,30]; % start point away from the minimum [xf,ff,flf,of] = fminunc(rf2,x0)
fminunc возвращается
Local minimum found.
Optimization completed because the size of the gradient is
less than the default value of the function tolerance.
xf =
19.8991 29.8486
ff =
12.9344
flf =
1
of =
struct with fields:
iterations: 3
funcCount: 15
stepsize: 1.7776e-06
lssteplength: 1
firstorderopt: 5.9907e-09
algorithm: 'quasi-newton'
message: 'Local minimum found.…'xf является точкой минимизации.
ff является значением цели, rf2, в xf.
flf является выходным флагом. Выходной флаг 1 указывает, что xf является локальным минимумом.
of является выходной структурой, которая описывает продвижение вычислений fminunc к решению.
Решить задачу оптимизации с помощью решателя Global Optimization Toolbox patternsearch, введите:
rf2 = @(x)rastriginsfcn(x/10); % objective x0 = [20,30]; % start point away from the minimum [xp,fp,flp,op] = patternsearch(rf2,x0)
patternsearch возвращается
Optimization terminated: mesh size less than options.MeshTolerance.
xp =
19.8991 -9.9496
fp =
4.9748
flp =
1
op =
struct with fields:
function: @(x)rastriginsfcn(x/10)
problemtype: 'unconstrained'
pollmethod: 'gpspositivebasis2n'
maxconstraint: []
searchmethod: []
iterations: 48
funccount: 174
meshsize: 9.5367e-07
rngstate: [1x1 struct]
message: 'Optimization terminated: mesh size less than options.MeshTolerance.'xp является точкой минимизации.
fp является значением цели, rf2, в xp.
flp является выходным флагом. Выходной флаг 1 указывает, что xp является локальным минимумом.
op является выходной структурой, которая описывает продвижение вычислений patternsearch к решению.
Решить задачу оптимизации с помощью решателя Global Optimization Toolbox ga, введите:
rng default % for reproducibility
rf2 = @(x)rastriginsfcn(x/10); % objective
x0 = [20,30]; % start point away from the minimum
initpop = 10*randn(20,2) + repmat([10 30],20,1);
opts = optimoptions('ga','InitialPopulationMatrix',initpop);
[xga,fga,flga,oga] = ga(rf2,2,[],[],[],[],[],[],[],opts)initpop 20 2 матрица. Каждая строка initpop имеет средний [10,30], и каждый элемент нормально распределен со стандартным отклонением 10. Строки initpop формируют начальную матрицу генеральной совокупности для решателя ga.
opts является опциями, которые устанавливают initpop как начальную генеральную совокупность.
Итоговая строка вызывает ga, с помощью опций.
ga использует случайные числа и приводит к случайному результату. В этом случае возвращается ga:
Optimization terminated: average change in the fitness value
less than options.FunctionTolerance.
xga =
0.0236 -0.0180
fga =
0.0017
flga =
1
oga =
struct with fields:
problemtype: 'unconstrained'
rngstate: [1x1 struct]
generations: 107
funccount: 5400
message: 'Optimization terminated: average change in the fitness value less...'
maxconstraint: []xga является точкой минимизации.
fga является значением цели, rf2, в xga.
flga является выходным флагом. Выходной флаг 1 указывает, что xga является локальным минимумом.
oga является выходной структурой, которая описывает продвижение вычислений ga к решению.
Как ga, particleswarm является основанным на генеральной совокупности алгоритмом. Таким образом для справедливого сравнения решателей, инициализируйте рой частицы той же генеральной совокупности как ga.
rng default % for reproducibility
rf2 = @(x)rastriginsfcn(x/10); % objective
opts = optimoptions('particleswarm','InitialSwarmMatrix',initpop);
[xpso,fpso,flgpso,opso] = particleswarm(rf2,2,[],[],opts)Optimization ended: relative change in the objective value
over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
xpso =
1.0e-06 *
-0.8839 0.3073
fpso =
1.7373e-12
flgpso =
1
opso =
struct with fields:
rngstate: [1x1 struct]
iterations: 114
funccount: 2300
message: 'Optimization ended: relative change in the objective value …'xpso является точкой минимизации.
fpso является значением цели, rf2, в xpso.
flgpso является выходным флагом. Выходной флаг 1 указывает, что xpso является локальным минимумом.
opso является выходной структурой, которая описывает продвижение вычислений particleswarm к решению.
surrogateopt не требует стартовой точки, но действительно требует конечных границ. Установите границы –70 к 130 в каждом компоненте. Чтобы иметь тот же вид вывода как другие решатели, отключите функцию построения графика по умолчанию.
rng default % for reproducibility
lb = [-70,-70];
ub = [130,130];
rf2 = @(x)rastriginsfcn(x/10); % objective
opts = optimoptions('surrogateopt','PlotFcn',[]);
[xsur,fsur,flgsur,osur] = surrogateopt(rf2,lb,ub,opts)Surrogateopt stopped because it exceeded the function evaluation limit set by
'options.MaxFunctionEvaluations'.
xsur =
-9.9516 -9.9486
fsur =
1.9899
flgsur =
0
osur =
struct with fields:
rngstate: [1×1 struct]
funccount: 200
elapsedtime: 3.0454
message: 'Surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'
xsur является точкой минимизации.
fsur является значением цели, rf2, в xsur.
flgsur является выходным флагом. Выходной флаг 0 указывает, что surrogateopt остановился, потому что это исчерпало функциональные оценки или время.
osur является выходной структурой, которая описывает продвижение вычислений surrogateopt к решению.
Решить задачу оптимизации с помощью решателя GlobalSearch, введите:
rf2 = @(x)rastriginsfcn(x/10); % objective
x0 = [20,30]; % start point away from the minimum
problem = createOptimProblem('fmincon','objective',rf2,...
'x0',x0);
gs = GlobalSearch;
[xg,fg,flg,og] = run(gs,problem)problem является структурой задачи оптимизации. problem задает решатель fmincon, целевую функцию rf2 и x0=[20,30]. Для получения дополнительной информации об использовании createOptimProblem смотрите, Создают Структуру задачи.
Необходимо задать fmincon как решатель для GlobalSearch, даже для неограниченных проблем.
gs является объектом GlobalSearch по умолчанию. Объект содержит опции для решения проблемы. Вызов run(gs,problem) запускает problem от нескольких стартовых точек. Стартовые точки случайны, таким образом, следующий результат также случаен.
В этом случае выполнение возвращается:
GlobalSearch stopped because it analyzed all the trial points.
All 4 local solver runs converged with a positive local solver exit flag.
xg =
1.0e-07 *
-0.1405 -0.1405
fg =
0
flg =
1
og =
struct with fields:
funcCount: 2128
localSolverTotal: 4
localSolverSuccess: 4
localSolverIncomplete: 0
localSolverNoSolution: 0
message: 'GlobalSearch stopped because it analyzed all the trial points.↵↵All 4 local solver runs converged with a positive local solver exit flag.'
xg является точкой минимизации.
fg является значением цели, rf2, в xg.
flg является выходным флагом. Выходной флаг 1 указывает, что все выполнения fmincon сходились правильно.
og является выходной структурой, которая описывает продвижение вычислений GlobalSearch к решению.
Одно решение лучше, чем другой, если его значение целевой функции меньше, чем другой. Следующая таблица обобщает результаты, с точностью до одного десятичного числа.
| Результаты | fminunc | patternsearch | ga | particleswarm | surrogateopt | GlobalSearch |
|---|---|---|---|---|---|---|
| решение | [19.9 29.9] | [19.9 -9.9] | [0 0] | [0 0] | [-9.9 -9.9] | [0 0] |
| цель | 12.9 | 5 | 0 | 0 | 2 | 0 |
| # Fevals | 15 | 174 | 5400 | 2300 | 200 | 2178 |
Эти результаты типичны:
fminunc быстро достигает локального решения в своем стартовом бассейне, но не исследует вне этого бассейна вообще. fminunc имеет простой синтаксис вызова.
patternsearch берет больше функциональных оценок, чем fminunc и перерывает несколько бассейнов, находя лучшее решение, чем fminunc. Синтаксис вызова patternsearch совпадает с синтаксисом fminunc.
ga берет намного больше функциональных оценок, чем patternsearch. Случайно это нашло лучшее решение. В этом случае ga нашел точку около глобального оптимума. ga является стохастическим, таким образом, его изменение результатов с каждым выполнением. ga имеет простой синтаксис вызова, но существуют дополнительные шаги, чтобы иметь начальную генеральную совокупность около [20,30].
particleswarm берет меньше функциональных оценок, чем ga, но больше, чем patternsearch. В этом случае particleswarm нашел глобальный оптимум. particleswarm является стохастическим, таким образом, его изменение результатов с каждым выполнением. particleswarm имеет простой синтаксис вызова, но существуют дополнительные шаги, чтобы иметь начальную генеральную совокупность около [20,30].
surrogateopt останавливается, когда он достигает функционального предела оценки, который по умолчанию является 200 для 2D переменной проблемы. surrogateopt имеет простой синтаксис вызова, но требует конечных границ. Несмотря на то, что surrogateopt пытается найти глобальное решение, в этом случае возвращенное решение не является глобальным решением. Каждая функциональная оценка в surrogateopt занимает более длительное время, чем в большинстве других решателей, потому что surrogateopt выполняет много вспомогательных вычислений как часть его алгоритма.
GlobalSearch
run берет тот же порядок величины функциональных оценок как ga и particleswarm, ищет много бассейнов и находит хорошее решение. В этом случае GlobalSearch нашел глобальный оптимум. Подготовка GlobalSearch более включена, чем подготовка других решателей. Когда пример показывает, прежде, чем вызвать GlobalSearch, необходимо создать обоих объект GlobalSearch (gs в примере), и структура задачи (problem). Затем вы вызываете метод run с gs и problem. Для получения дополнительной информации о том, как запустить GlobalSearch, смотрите Рабочий процесс для GlobalSearch и MultiStart.