Вы идентифицируете модель так, чтобы можно было точно вычислить ответ динамической системы на вход. Существует два способа сгенерировать идентифицированный образцовый ответ:
Simulation вычисляет образцовый ответ с помощью входных данных и начальных условий.
Prediction вычисляет образцовый ответ в некотором заданном количестве времени в будущем с помощью текущих и прошлых значений измеренных значений ввода и вывода, а также начальных условий.
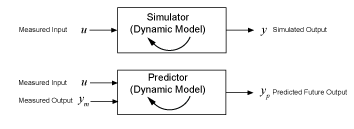
В системе идентификации цель состоит в том, чтобы создать реалистическую модель динамической системы, которая может затем использоваться или передаваться для цели приложения. В этом контексте основные роли симуляции и прогноза в System Identification Toolbox™ должны обеспечить инструменты для образцовой идентификации, и также для выбора, настройки и проверки этих моделей.
Вы можете:
Идентифицируйте свою модель способом, который минимизирует или прогноз (prediction focus) или ошибку симуляции (simulation focus)
Визуализируйте свой образцовый ответ по сравнению с другими моделями и с измерениями данных
Подтвердите свою модель путем сравнения ее ответа с измеренными данными о вводе/выводе, которые не использовались для исходной образцовой оценки
Ваш выбор симуляции или подхода прогноза зависит от того, что ваши потребности приложения, но также и где вы находитесь в рабочем процессе системы идентификации:
Когда вы идентифицируете свои модели, особое внимание прогноза с одним шагом обычно приводит к лучшим результатам. Это преимущество состоит в том, потому что при помощи обоих измерений ввода и вывода прогноз с одним шагом составляет природу воздействий. Составление воздействий обеспечивает наиболее статистически оптимальные результаты.
Когда вы подтверждаете свои модели, симуляция обычно обеспечивает более проницательный подход для оценки, как ваша модель выполнит под широким спектром условий. Ваше приложение может управлять основанной на прогнозе валидацией также, как бы то ни было. Например, если вы планируете использовать свою модель для системы управления, можно подтвердить модель путем предсказания ее ответа за период времени, который представляет временные константы доминирования модели.
Можно работать или во временном интервале или в частотном диапазоне, и остаться сопоставимыми с областью данных о вводе/выводе. Для данных частотного диапазона результаты симуляции являются продуктами преобразования Фурье входа и функции частоты модели. Поскольку идентификация модели частотной характеристики игнорирует шумовую динамику, особое внимание симуляции и особое внимание прогноза с одним шагом приводят к той же идентифицированной модели. Для валидации в частотном диапазоне используйте симуляцию.
Для примеров см.:
Можно получить более подробное понимание различий между симуляцией и прогнозом путем применения этих методов к простой системе первого порядка.
Simulation означает вычислять образцовый ответ с помощью входных данных и начальных условий. Выборки времени образцового ответа совпадают с выборками времени входных данных, используемых для симуляции. Другими словами, учитывая входные параметры u (t 1, …, tN), симуляция генерирует y (t 1, …, tN). Следующая схема иллюстрирует этот поток.

Для непрерывно-разовой системы симуляция означает решать дифференциальное уравнение. Для системы дискретного времени симуляция означает непосредственно применение образцовых уравнений.
Например, считайте динамическую модель описанной разностным уравнением первого порядка, которое использует шаг расчета 1 секунды:
y (t +1) = a y (t) + b u (t),
где y является вывод, и u является входом.
Эта система эквивалентна следующей блок-схеме.
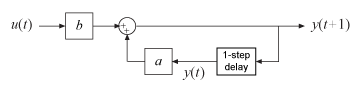
Предположим, что ваша образцовая идентификация предоставляет вам предполагаемые значения параметров a = 0.9 и b = 1.5. Затем уравнение становится:
y (t +1) = 0.9y (t) + 1.5u (t).
Теперь предположите, что вы хотите вычислить значения y (1), y (2), y (3)... для данных входных значений u (0) = 2, u (1) = 1, u (2) = 4, … Здесь, y (1) является значением вывода в первый момент выборки. Используя начальное условие y (0) = 0, значения y (t) в течение многих времен t = 1, 2, и 3 может быть вычислен как:
y (1) = 0.9y (0) + 1.5u (0) = (0.9) (0) + (1.5) (2) = 3
y (2) = 0.9y (1) + 1.5u (1) = (0.9) (3) + (1.5) (1) = 4.2
y (3) = 0.9y (2) + 1.5u (2) = (0.9) (4.2) + (1.5) (4) = 9.78
Prediction означает проектировать образцовый ответ, k продвигается вперед в будущее с помощью текущих и прошлых значений измеренных значений ввода и вывода. k называется prediction horizon и соответствует предсказанию вывода во время k Ts, где Ts является шагом расчета. Другими словами, учитывая измеренные входные параметры um (t 1, …, t N +k) и измеренные выходные параметры ym (t 1, …, t N), прогноз генерирует yp (tN+k).
Например, предположите, что вы используете датчики, чтобы измерить входной сигнал um (t) и выходной сигнал ym (t) физической системы, описанной в предыдущем уравнении первого порядка. Уравнение становится:
yp (t +1) = a ym (t) + b um (t),
где y является вывод, и u является входом.
Версия предиктора предыдущей блок-схемы симуляции:
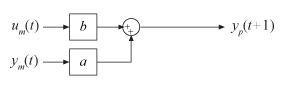
В 10-й момент выборки (t = 10), измеренный вывод ym (10) составляет 16 мм, и соответствующий вход um (10) составляет 12 Н. Теперь, вы хотите предсказать значение вывода в будущее время t = 11. Используя предыдущее уравнение, предсказанный вывод yp:
yp (11) = 0.9ym (10) + 1.5um (10)
Следовательно, ожидаемое значение будущего вывода y (11) во время t = 10:
yp (11) = 0.9*16 + 1.5*12 = 32.4
В целом чтобы предсказать образцовый ответ k продвигается в будущее (k ≥1) с текущего времени t, необходимо знать входные параметры до времени t +k и выходные параметры до времени t:
yp (t +k) = f (um (t +k), um (t +k–1)..., um (t), um (t –1)..., um (0),
ym (t), ym (t –1), ym (t –2)..., ym (0))
um (0) и ym (0) являются начальными состояниями. f() представляет predictor, который является динамической моделью, форма которой зависит от образцовой структуры.

Предиктор "один шаг вперед" от предыдущего примера, yp модели y (t) + a y (t –1) = b u (t):
yp (t +1) = –ayp (t) + b um (t +1)
В этом простом случае предиктора с одним шагом новейший прогноз базируется только на измерениях. Для предикторов нескольких-шагов динамическая модель распространяет состояния внутренне, с помощью предыдущих предсказанных состояний в дополнение к входным параметрам. Каждый предсказанный вывод поэтому является результатом комбинации измеренного входа и выходных параметров и предыдущих предсказанных выходных параметров.
Можно установить k на любое положительное целочисленное значение до количества выборок результатов измерений. Если вы устанавливаете k на ∞, то никакие предыдущие выходные параметры не используются в вычислении прогноза, и прогноз возвращает тот же результат как симуляция. Если вы устанавливаете k на целое число, больше, чем количество выборок данных, predict устанавливает k на Inf и выдает предупреждение. Если ваше намерение состоит в том, чтобы выполнить прогноз в области значений времени вне прошлого момента результатов измерений, используйте forecast.
Для прогноза показа в качестве примера и симуляции в MATLAB®, смотрите, Сравнивают Предсказанный и Моделируемый Ответ Идентифицированной Модели к Результатам измерений.
Не все модели поддерживают прогнозирующий подход. Для предыдущей динамической модели, , структура поддерживает использование прошлых данных. Эта поддержка не существует в моделях структуры Ошибки на выходе (OE) (H (z) = 1). Нет никакой информации в мимо выходных параметров, которые могут использоваться для предсказания будущих выходных значений. В этих случаях совпадают прогноз и симуляция. Даже модели, которые обычно используют прошлую информацию, могут все еще иметь структуру OE в особых случаях. Модели в пространстве состояний (idss) имеют структуру OE когда K=0. Полиномиальные модели (idpoly) также имеют структуру OE, когда a=c=d=1. В этих особых случаях прогноз и симуляция эквивалентны, и возмущение фиксируется к 1.
Этот пример показывает, как визуализировать и предсказанный образцовый ответ и моделируемый образцовый ответ идентифицированной линейной модели.
Идентифицируйте модель в пространстве состояний третьего порядка с помощью измерений ввода/вывода в z1.
load iddata1 z1; sys = ssest(z1,3);
sys является непрерывно-разовой идентифицированной моделью (idss) пространства состояний. Здесь, sys идентифицирован с помощью особого внимания прогноза с 1 шагом по умолчанию, которое минимизирует ошибку прогноза с 1 шагом. Это особое внимание обычно предоставляет лучшую полную модель.
Теперь используйте compare, чтобы построить предсказанный ответ. В данном примере установите горизонт прогноза kstep на 10 шагов и используйте compare, чтобы построить предсказанный ответ против исходных данных об измерении. Эта установка kstep указывает, что каждая точка ответа является 10 шагами в будущем относительно данных об измерении, используемых, чтобы предсказать ту точку.
kstep = 10; figure compare(z1,sys,kstep)

В этом графике каждая точка данных представляет предсказанный вывод, сопоставленный с выходными данными об измерении, которые были сделаны по крайней мере 10 шагов ранее. Например, точка в t=15 секунды основана на измерениях, проведенных в или до t=5 секунд.
График иллюстрирует различия между образцовым ответом и исходными данными. Процент в легенде является значением фитнеса NRMSE. Это представляет, как тесно предсказанная модель выводила соответствия данные.
Чтобы улучшить ваши результаты, можно уменьшать горизонт прогноза.
kstep = 5; figure compare(z1,sys,kstep)

Значение фитнеса NRMSE улучшилось от значения фитнеса, полученного в случае с 10 шагами. В реальном приложении существуют различные факторы, которые влияют, насколько маленький горизонт прогноза может быть. Они включают временные константы и требования предвидения приложения.
Можно просмотреть моделируемый ответ для сравнения, а не предсказанный ответ, при помощи значения по умолчанию kstep для compare, который является Inf. С симуляцией вычисление ответа использует только входные данные, не измеренные выходные данные.
figure compare(z1,sys)

Моделируемый и предсказанные ответы с 10 шагами приводят к подобным полным подходящим процентам.
Чтобы изменить параметры экрана в графике, щелкните правой кнопкой по графику получить доступ к контекстному меню. Например, чтобы построить ошибку между предсказанным выводом и измеренным выводом, выберите Error Plot из контекстного меню.
Этот пример показывает, как идентифицировать модели с особым вниманием прогноза и с особым вниманием симуляции. Сравните ответы особого внимания прогноза и моделей особого внимания симуляции против исходных данных об оценке, и против данных о валидации, которые не использовались для оценки.
Когда вы идентифицируете модель, алгоритм использует опцию 'Focus', чтобы определить, минимизировать ли ошибку прогноза или ошибку симуляции. Значением по умолчанию является 'prediction'. Можно изменить это путем изменения опции 'Focus' на 'simulation'.
Загрузите данные об измерении z1 и разделите его на две половины z1e и z1v. Одна половина используется для образцовой идентификации и другой половины для проверки допустимости модели.
load iddata1 z1; %z1e = z1(1:150); %To avoid ordqz stall %z1v = z1(151:300); z1e = z1(1:155); z1v = z1(156:300);
Идентифицируйте модель в пространстве состояний третьего порядка sys_pf с помощью измерений ввода/вывода в z1e. Используйте опцию опции по умолчанию 'Focus' для этой модели, которая является 'прогнозом'.
sys_pf = ssest(z1e,3);
sys_pf является непрерывно-разовой идентифицированной моделью (idss) пространства состояний.
Используя тот же набор данных об измерении, идентифицируйте вторую модель в пространстве состояний sys_sf, который устанавливает 'Focus' на 'simulation'.
opt = ssestOptions('Focus','simulation'); sys_sf = ssest(z1e,3,opt);
Используйте функцию compare, чтобы моделировать ответ на обе идентифицированных модели.
figure compare(z1e,sys_pf,sys_sf)

Модель, идентифицированная с прогнозирующим особым вниманием, имеет более высокое значение подгонки NRMSE, чем модель, идентифицированная с особым вниманием симуляции.
Теперь выполните сравнение с данными о валидации. Это сравнение показывает, как хорошо модель выполняет с условиями, которые не были частью ее идентификации.
figure compare(z1v,sys_pf,sys_sf)

Подходящие значения для обеих моделей улучшаются. Однако модель с особым вниманием прогноза остается выше, чем модель с особым вниманием симуляции.
compare | forecast | predict | sim