Моделируйте ответ идентифицированной модели
y = sim(sys,udata)y = sim(sys,udata,opt)[y,y_sd] = sim(___)[y,y_sd,x]
= sim(___)[y,y_sd,x,x_sd] = sim(___)sim(___)sim(___) строит моделируемый ответ идентифицированной модели.
Когда начальные условия предполагаемой модели и системы, которая измерила набор данных валидации, отличаются, моделируемые и измеренные ответы могут также отличаться, особенно в начале ответа. Чтобы минимизировать это различие, оцените значения начального состояния с помощью findstates и используйте ориентировочные стоимости, чтобы установить опцию InitialCondition с помощью simOptions. Для примера смотрите Ответ Модели Соответствия на Выходные данные.
Симуляция означает вычислять образцовый ответ с помощью входных данных и начальных условий. sim моделирует следующую систему:
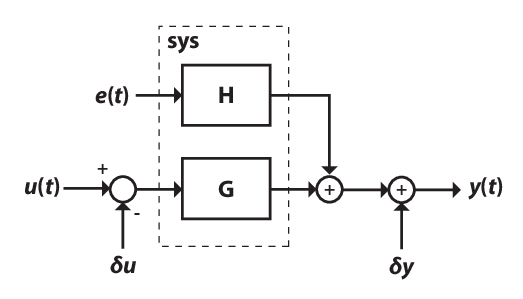
Здесь,
u (t) является входными данными симуляции, udata.
y (t) является моделируемым выходным ответом.
G является передаточной функцией от входа до вывода и задан в sys. Начальные условия симуляции, как задано использование simOptions, устанавливают начальное состояние G.
e (t) является дополнительным шумовым сигналом. Добавьте шум в свою симуляцию путем создания набора опции simOptions и установки опции AddNoise на true. Кроме того, можно изменить шумовой сигнал по умолчанию путем определения опции NoiseData.
H является шумовой передаточной функцией и задан в sys.
δu является дополнительным входным смещением, вычтенным из входного сигнала, u (t), прежде чем вход будет использоваться, чтобы моделировать модель. Задайте вход, смещенный путем установки опции InputOffset с помощью simOptions.
δy является дополнительным выходным смещением, добавленным к выходному ответу, y (t), после симуляции. Задайте вывод, смещенный путем установки опции OutputOffset с помощью simOptions.
Для получения дополнительной информации об определении начальных условий симуляции смещения ввода и вывода и шумовые данные сигнала, видят simOptions. Для данных о мультиэксперименте можно задать эти опции отдельно для каждого эксперимента.
Используйте simsd для метода Монте-Карло вычисления стандартного отклонения ответа.
sim расширяет lsim, чтобы упростить дополнительные функции, относящиеся к идентифицированным моделям:
Симуляция нелинейных моделей
Симуляция с аддитивным шумом
Объединение смещений сигнала
Вычисление стандартного отклонения ответа (только линейные модели)
Симуляция частотного диапазона (только линейные модели)
Симуляции с помощью различного междемонстрационного поведения для различных входных параметров
Чтобы получить моделируемый ответ без любой из предыдущих операций, используйте lsim.
compare | findstates | forecast | idinput | lsim | predict | simOptions | simsd | step