Когда вы моделируете динамическую систему, которая не начинает с отдыха, необходимо инициализировать ту симуляцию, чтобы совпадать со стартовыми условиями. Например, можно сравнивать моделируемый ответ на результаты измерений, или на предыдущую симуляцию или вычисление. Вы можете хотеть запустить свою симуляцию при установившемся условии или продолжить симуляцию от предыдущей симуляции.
System Identification Toolbox™ обеспечивает несколько методов для определения начальных условий (ICS), чтобы использовать. Эти методы включают использование:
Образцовые идентификационные результаты
Текущие или прошлые измерения данных о вводе/выводе
Информация состояния от предыдущих симуляций
Следующая таблица обобщает, какие подходы доступны и когда использовать их. Для краткости эта таблица использует термин "симуляция" широко, чтобы означать "моделировать или предсказывать". Для получения дополнительной информации смотрите, Моделируют и Предсказывают Идентифицированный Образцовый Вывод.
Подходы для оценки начальных условий
| Когда использовать | Подход | Сводные данные метода |
|---|---|---|
Вы моделируете ответ модели idss или idgrey с помощью тех же входных данных, с которыми вы идентифицировали свою модель. | Извлеките ICS от образцовых идентификационных результатов (возвращенные значения, или отчет оценки) — смотрите Оценочные Начальные условия от Результатов измерений. Используйте для моделей idss и idgrey только. | [sys,x0est] = ssest(z,__)[sys,x0est] = n4sid(z,__)[sys,x0est] = greyest(z,__)x0est = sys.Report.Parameters.X0пример: Разрешите Подходящие Различия в Значении Между Образцовой Идентификацией и сравните Команду |
Вы хотите воспроизвести результаты, сгенерированные compare (или эквивалентно графиком Model Output в приложении). | Используйте возвращенный ICS от compare — Смотрите Оценочные Начальные условия от Результатов измерений. | [y,x0,fit] = compare(sys,z)пример: Соответствуйте Вывод сравнивают Команду и Нелинейный блок Model ARX |
| Вы - ответ имитационной модели на данный входной сигнал и хотите запустить симуляцию в точке, которая приводит к самому близкому соответствию к данному выходному сигналу. | findstates
Если исходной моделью является idtf, idproc или idpoly, сначала преобразуйте в форму пространства состояний с помощью idss. Смотрите Оценочные Начальные условия для Симуляции Линейных Моделей.Для получения дополнительной информации смотрите Оценочные Начальные условия от Результатов измерений. | sys_ss = idss(sys)
x0 = findstates(sys_ss,z)пример: Оцените Начальные условия для Линейной Модели Используя Результаты измерений |
| Вы продолжаете симуляцию, такой что касается онлайновой обработки. Вы используете набор данных разделения, такой что касается модели nlarx, когда findstates является слишком в вычислительном отношении дорогим. | data2state
Если исходной моделью является idtf, idproc или idpoly, преобразуйте в форму пространства состояний сначала использование idss. Можно также использовать data2state неявно путем определения прошлых данных как прокси для начальных условий при использовании sim или predict с любой динамической моделью.Для получения дополнительной информации смотрите Оценочные Начальные условия от Результатов измерений. | sys_ss = idss(sys)x0 = data2state(sys,z_p)или IO = struct или opt = predictOptions ('InitialCondition',IO). примеры: Оцените Начальные условия для Нелинейной Модели ARX, Поймите использование исторических данных для симуляции модели |
| Вы работаете с продолжающейся симуляцией и хотите основывать начальные условия для текущего сегмента симуляции на предыдущем сегменте. Вы намереваетесь запустить свою основную симуляцию в устойчивом состоянии, и вы хотите иметь приквел, который моделирует подготовительный период к устойчивому состоянию от отдыха. | Используйте информацию состояния от предыдущей симуляции или предварительной симуляции. Если исходной моделью является idtf, idproc или idpoly, преобразуйте в форму пространства состояний сначала использование idss. Для получения дополнительной информации смотрите Начальные условия Использования от Прошлой информации состояния. | sys_ss = idss(sys)x0 = x(end) от [y,y_sd,x] = sim(sys_ss,z_p)пример: Продолжите Симуляцию Идентифицированной Модели с помощью Прошлых состояний |
Предыдущая таблица вызывает различные методы для оценки начального условия. Следующие разделы обобщают эти методы источником данных оценки.
Оцените начальные условия от данных об измерении, от которых вы получаете свои входные параметры симуляции. Методы включают:
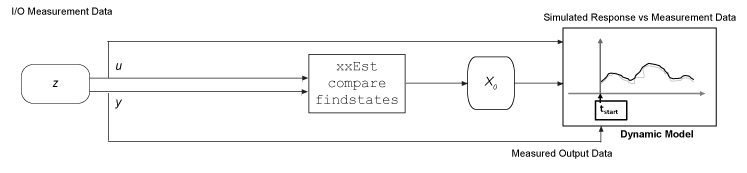
Извлеките начальные условия от результатов образцовой идентификации, такой как из идентификационного отчета для вашей модели или как возвращенные значения от compare. Для примеров смотрите Различия в Значении Подгонки Твердости Между Образцовой Идентификацией и сравните Команду и Соответствие, Вывод сравнивает Команду и Нелинейный блок Model ARX.
Оцените начальные условия с помощью измеренных данных о вводе/выводе, с помощью функционального findstates, чтобы оценить начальные состояния, сопоставимые с набором данных. Для примера смотрите Оценочные Начальные условия для Линейной Модели Используя Результаты измерений.
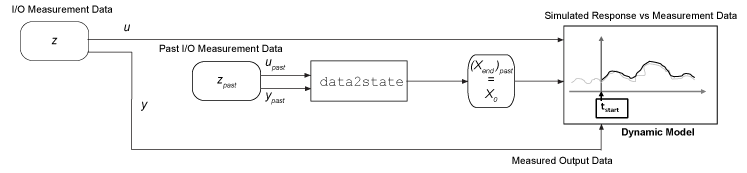
Оцените, что начальные условия от данных об измерении, сразу предшествующих вашей симуляции, запускаются. Методы включают:
Используя функциональный data2state, чтобы оценить то конечное состояние набора данных. Прошлое конечное состояние затем становится начальным состоянием для последующей симуляции. Для примера смотрите Оценочные Начальные условия для Нелинейной Модели ARX.
Используя ваши прошлые данные как прокси для начальных условий при использовании sim или predict. Когда вы запускаете свою симуляцию, модель внутренне вызывает data2state для вас. Для примера смотрите, Понимают Использование Исторических данных для Симуляции модели.
При разделении набора данных вы используете в две части. Сделайте первую часть только достаточно большой, чтобы позволить data2state вычислять точное конечное состояние. Этот подход данных разделения может быть намного менее в вычислительном отношении интенсивным, чем использование findstates на полном наборе данных, специально для нелинейных моделей ARX. Для примера смотрите Оценочные Начальные условия для Нелинейной Модели ARX.
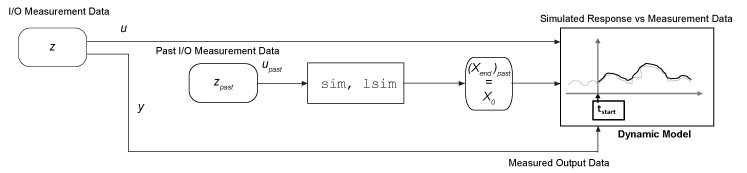
Используйте информацию состояния от предыдущих симуляций или предварительных симуляций. Если никакая предыдущая симуляция не доступна, можно предварительно моделировать от отдыха, или известное начальное условие на грани симуляции запускаются. Конечное состояние прошлого или предварительной симуляции является начальными состояниями для симуляции, которую вы хотите выполнить. Для примера смотрите, Продолжают Симуляцию Идентифицированной Модели с помощью Прошлых состояний.
findstates и функции data2state являются наиболее общими средствами для определения начальных состояний или конечного состояния от любых измерений данных о вводе/выводе. Однако использование их требует, чтобы вы использовали образцовую структуру, которая включает явное представление состояния. Линейные модели кроме idss и idgrey не используют явные состояния. Чтобы найти эквивалентные начальные состояния, можно преобразовать эти модели в модели idss и найти начальные состояния от версий idss.
После того, как вы оценили начальные условия, можно включить их в синтаксис симуляции командной строки, модель Simulink® или приложение System Identification.
Следующие примеры иллюстрируют оценку начального условия для линейных моделей. Первый пример использует findstates. Вторые и третьи примеры используют исторические данные. Таким образом, примеры определяют начальные условия от данных, сразу предшествующих времени начала симуляции.
Идентифицируйте модель idtf с помощью результатов измерений. Преобразуйте его в форму пространства состояний, чтобы оценить начальные условия, сопоставимые с этим результаты измерений. Затем выполните ту же оценку начального условия неявно на исходной модели idtf с помощью compare, чтобы видеть, получаете ли вы те же результаты.
Оцените передаточную функцию для результатов измерений.
load iddata1 z1; sys = tfest(z1,3);
sys является непрерывно-разовой идентифицированной моделью (idtf) передаточной функции.
Можно использовать findstates, чтобы найти начальные условия для линейных моделей, но только если они находятся в форме idgrey или idss.
Преобразуйте sys в форму пространства состояний.
sys_ss = idss(sys);
Используйте findstates, чтобы оценить начальные состояния.
X0 = findstates(sys_ss,z1)
X0 = 3×1
-1.7569
2.6195
-6.5177
Теперь используйте compare, чтобы оценить начальные состояния, с помощью исходной модели передаточной функции.
[y_tf,fit,X0c] = compare(z1,sys); X0c
X0c = 3×1
-1.7569
2.6195
-6.5177
Ответы идентичны. Этот результат состоит в том, потому что compare внутренне вызывает idss и findstates точно таким же образом, как вы сделали в первой части примера.
Используйте исторические данные ввода - вывода в качестве прокси для начальных условий при симуляции модели. Вы сначала моделируете использование команды sim и задаете исторические данные с помощью набора опции simOptions. Вы затем воспроизводите моделируемый вывод путем ручного отображения исторических данных с начальными состояниями.
Загрузите 2D вход, набор данных с одним выходом.
load iddata7 z7
Идентифицируйте модель в пространстве состояний пятого порядка с помощью данных.
sys = n4sid(z7,5);
Разделите набор данных в две части.
zA = z7(1:15); zB = z7(16:end);
Моделируйте модель с помощью входного сигнала в zB.
uSim = zB;
Симуляция требует начальных условий. Значения сигналов в zA являются историческими данными, то есть, они - значения ввода и вывода в течение времени, сразу предшествующего данным в zB. Используйте zA в качестве прокси для необходимых начальных условий.
IO = struct('Input',zA.InputData,'Output',zA.OutputData); opt = simOptions('InitialCondition',IO);
Моделируйте модель.
ysim = sim(sys,uSim,opt);
Теперь воспроизведите вывод путем ручного отображения исторических данных с начальными состояниями sys. Для этого используйте команду data2state.
xf = data2state(sys,zA);
xf содержит значения состояния sys в то время момент сразу после новой выборки данных в zA.
Моделируйте систему с помощью xf в качестве начальных состояний.
opt2 = simOptions('InitialCondition',xf);
ysim2 = sim(sys,uSim,opt2);Постройте вывод команды sim ysim и вручную вычисленные результаты ysim 2.
plot(ysim,'b',ysim2,'--r')

ysim2 совпадает с ysim.
Оцените начальные условия для сегмента симуляции идентифицированной модели при помощи конечного состояния предыдущего сегмента симуляции.
Загрузите данные z1, который является объектом iddata, содержащим входные и выходные данные. Оцените пятый порядок линейная модель от данных.
load iddata1 z1 plot(z1)

sys = n4sid(z1,5);
Разделите данные на два сегмента. Один сегмент z1past представляет данные для прошлой симуляции и запускается в покое. Второй сегмент z1next представляет данные для последующей симуляции.
z1past = z1(1:150); z1next = z1(150:300);
Моделируйте ответ на входные данные в z1next, не задавая начальные условия.
ynext_no_ic = sim(z1next,sys);
plot(ynext_no_ic,z1next)
legend
title('Simulation Continuation Without Setting ICs')
Теперь определите конечное состояние, x0, для ответа на z1past input.
[ypast,y_sd,xpast] = sim(z1past,sys); x0 = xpast(end,:)';
Используйте конечное состояние, чтобы задать начальные состояния для последующего ответа на z1next.
opt = simOptions('InitialCondition',x0); ynext_ic = sim(z1next,sys,opt); figure plot(ynext_ic,z1next) legend title('Simulation Continuation with Sychronized ICs')

Когда вы моделируете Хаммерстайна-Винера или нелинейную модель серого поля и захотите использовать начальные условия, сопоставимые с набором данных измерения z, используйте findstates.
Сравните моделируемый вывод блока Model Хаммерстайна-Винера к измеренному выводу системы. Вы улучшаете соглашение между измеренными и моделируемыми ответами путем оценки значений начального состояния.
Загрузите выборочные данные.
load twotankdata
Создайте объект iddata из выборочных данных. Установите 'Tstart' на 0 так, чтобы время начала данных совпадало со временем начала Simulink 0f 0 с.
z1 = iddata(y,u,0.2,'Tstart',0,'Name','Two tank system');
Оцените модель Хаммерстайна-Винера использование данных.
mw1 = nlhw(z1,[1 5 3],pwlinear,pwlinear);
Можно теперь моделировать вывод предполагаемой модели в Simulink с помощью входных данных в z1. Для этого откройте предварительно сконфигурированную модель Simulink.
model = 'ex_idnlhw_block';
open_system(model);

Модель использует Источник Iddata, Модель Хаммерстайна-Винера и блоки Осциллографа. Следующие параметры блоков были предварительно сконфигурированы, чтобы задать данные об оценке, оцененную модель и начальные условия:
Параметры блоков Исходного блока Iddata:
Объект IDDATA - z1
Параметры блоков блока Model Хаммерстайна-Винера:
Модель - mw1
Начальные условия - Zero (значение по умолчанию)
Запустите симуляцию.
Просмотрите различие между измеренным выводом и образцовым выводом при помощи блока Scope.
simOut = sim(model);
open_system([model '/Scope'])

Чтобы улучшить соглашение между измеренными и моделируемыми ответами, оцените вектор начального состояния для модели от данных об оценке z1, с помощью findstates. Задайте максимальное количество итераций для оценки как 100. Задайте горизонт прогноза как Inf, так, чтобы алгоритм вычислил начальные состояния, которые минимизируют ошибку симуляции.
opt = findstatesOptions; opt.SearchOptions.MaxIterations = 100; x0 = findstates(mw1,z1,Inf,opt);
Установите значение параметров блоков Начальных условий блока Model Хаммерстайна-Винера к State Values. Начальными состояниями по умолчанию является x0.
set_param([model '/Hammerstein-Wiener Model'],'IC','State values');
Запустите симуляцию снова и просмотрите различие между измеренным выводом и образцовым выводом в блоке Scope. Различие между измеренными и моделируемыми ответами теперь уменьшается.
simOut = sim(model);

Когда вы моделируете нелинейную модель ARX и хотите использовать начальные условия, сопоставимые с набором данных измерения z, у вас есть выбор для который подход взять.
Можно использовать findstates. Для нелинейных моделей ARX однако, этот подход имеет стоимость того, чтобы быть в вычислительном отношении дорогим, если набор данных является большим.
X0 = findstates(m,z,Inf);
Можно повредить набор данных в два фрагмента. Используйте первые выборки nx данных о вводе/выводе как прошлые данные, где nx является самой большой задержкой регрессора модели. Затем используйте data2state, чтобы вычислить конечное состояние "прошлых данных". Вы затем можете моделировать модель для остающихся входных данных nx+1:end с любым подходом симуляции, который вы выбираете. И compare и приложение System Identification используют этот подход автоматически для нелинейных моделей ARX.
nx = max(getDelayInfo(m)); % Find the largest regressor delay
past_data = z1(1:nx);
X0 = data2state(mw1,z1(1:nx));Следующий пример иллюстрирует использование метода данных разделения для нелинейной модели ARX.
Используйте два различных метода, чтобы оценить начальные условия для нелинейной модели ARX. Моделируйте каждого вместе с данными об измерении и сравните с симуляцией, которая инициализирует в покое.
Загрузите данные о вводе/выводе z и постройте его. Используйте первые 1 000 точек z, чтобы оценить нелинейную модель ARX.
load twotankdata z = iddata(y,u,0.2); z1 = z(1:1000); plot(z1) title('Estimation data')

mdlnlarx = nlarx(z1,[5 1 3],wavenet);
Извлеките первые 250 точек z1 (50 секунд) как z1sim для симуляций сравнения. Моделируйте mdlarx, не устанавливая начальные условия и постройте ответ вместе с измеренным выводом в z1sim.
z1sim = z1(1:250); data_no_ic = sim(mdlnlarx,z1sim); plot(data_no_ic,z1sim) title('Nonlinear ARX Model with No Initial Condition Setting') grid on legend('location','se')

Используйте findstates, чтобы оценить начальные условия. В порядке минимизировать ошибку симуляции, задайте Inf для горизонта прогноза. Затем установите опцию sim для InitialCondition к результатам findstates. Постройте ответ вместе с измеренным выводом.
x0fs = findstates(mdlnlarx,z1sim,Inf); opt = simOptions('InitialCondition',x0fs); data_fs = sim(mdlnlarx,z1sim,opt); figure plot(data_fs,z1sim) title('Nonlinear ARX Model with IC Estimation Using findstates') grid on legend('location','se')

Ответ и измеренный вывод теперь запускаются примерно в той же точке.
Теперь используйте метод data2states, чтобы оценить начальные условия. Во-первых, повредите набор данных в два фрагмента. Используйте первые выборки nx z1sim как "прошлые данные", где nx является самой большой задержкой регрессора модели.
nx = max(getDelayInfo(mdlnlarx))
nx = 5
z1past = z1sim(1:nx); z1sim2 = z1sim(nx+1:end);
Используйте data2state, чтобы вычислить конечное состояние "прошлых данных". Моделируйте вход использования ответа, запускающийся в z1sim(nx+1). Постройте ответ вместе с полными данными об измерении z1sim так, чтобы можно было соответствовать графику findstates.
x0d2s = data2state(mdlnlarx,z1past); opt = simOptions('InitialCondition',x0d2s); data_d2s = sim(mdlnlarx,z1sim2,opt); figure plot(data_d2s,z1sim) title('Nonlinear ARX Model with IC Estimation Using data2state') grid on legend('location','se')

Если вы выполнили каждый раздел отдельно, можно найти что метод data2states завершенный более быстро, чем метод findstates.
Теперь сравните ответы для всех трех случаев начального условия.
plot(data_fs,data_d2s,data_no_ic) title('Nonlinear ARX model Responses for Three IC Approaches Compared') legend('location','se')

Ответы для случаев с помощью findstates и data2state являются фактически тем же самым. Ответ для случая, где начальные условия не были установлены, сходится в конечном счете, но только когда после 30 секунд.
compare | compareOptions | data2state | findstates | predict | predictOptions | sim | simOptions