Оценка состояния контроллера

Переменные состояния контроллера

Когда контроллер действует, это использует свое текущее состояние, _xc, как основание для прогнозов. По определению вектор состояния следующий:

$x_{c}^{T} (k) = [\begin{matrix} x_{p}^{T} (k) & x_{i d}^{T} (k) & \begin{matrix} x_{o d}^{T} (k) & x_{n}^{T} (k) \end{matrix} \end{matrix}] .$

Здесь,

_xc является состоянием контроллера, включая _nxp + _nxid + _nxod + переменные состояния _nxn.
_xp является вектором состояния модели объекта управления длины _nxp.
_xid является входным вектором состояния возмущения длины _nxid.
_xod является выходным вектором состояния возмущения длины _nxod.
_xn является шумом измерения образцовый вектор состояния длины _nxn.

Таким образом переменные, включающие _xc, представляют модели, появляющиеся в следующей схеме системы MPC.

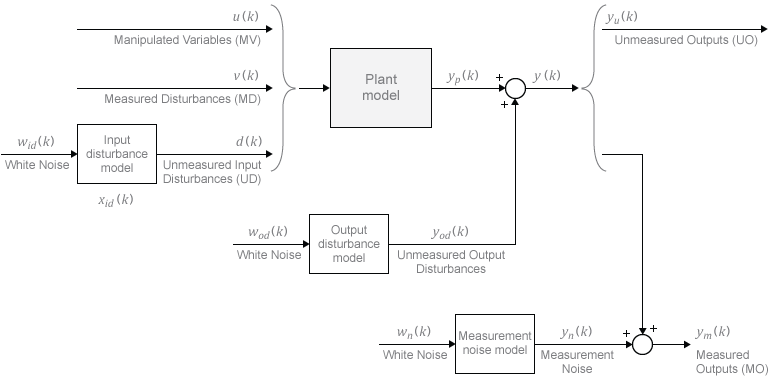
Некоторые векторы состояния могут быть пустыми. В противном случае они появляются в последовательности, заданной в каждой модели.

По умолчанию контроллер обновляет его состояние автоматически с помощью последних измерений объекта. Смотрите Оценку состояния для деталей. Также пользовательская функция оценки состояния позволяет вам обновлять состояние контроллера использование внешней процедуры, и затем предоставлять эти значения контроллеру. Смотрите Пользовательскую Оценку состояния для деталей.

Наблюдатель состояния

Комбинация моделей, показанных в схеме, приводит к наблюдателю состояния:

$\begin{matrix} x_{c} (k + 1) = A x_{c} (k) + B u_{o} (k) \\ y (k) = C x_{c} (k) + D u_{o} (k) . \end{matrix}$

Диспетчер MPC использует наблюдателя состояния следующими способами:

Оценить значения неизмеренных состояний, необходимых как основание для прогнозов (см. Оценку состояния).
Предсказать, как предложенные корректировки переменной, которой управляют, (MV) диспетчера будут влиять на будущие выходные значения объекта (см. Прогноз Выходной переменной).

Входные сигналы наблюдателя являются безразмерным объектом которыми управляют и измеренные входные параметры воздействия, и белые шумовые входные параметры к воздействию и шумовые модели:

$u_{o}^{T} (k) = [\begin{matrix} u^{T} (k) & v^{T} (k) & \begin{matrix} \begin{matrix} w_{i d}^{T} (k) & w_{o d}^{T} (k) \end{matrix} & w_{n}^{T} (k) \end{matrix} \end{matrix}] .$

Выходными параметрами наблюдателя является _ny безразмерный объект выходные параметры.

С точки зрения параметров, задающих эти четыре модели, показанные в схеме, параметры наблюдателя:

$\begin{matrix} A = [\begin{matrix} A_{p} & B_{p d} C_{i d} \\ 000 & A_{i d} \\ 0000 & A_{o d} \\ 0000 & A_{n} \end{matrix}], & B = [\begin{matrix} B_{p u} & B_{p v} & B_{p d} D_{i d} \\ 0000 & B_{i d} \\ 00000 & B_{o d} \\ 00000 & B_{n} \end{matrix}] \\ C = [\begin{matrix} C_{p} & D_{p d} C_{i d} & C_{o d} & [\begin{matrix} C_{n} \\ 0 \end{matrix}] \end{matrix}], & D = [\begin{matrix} 0 & D_{p v} & D_{p d} D_{i d} & D_{o d} & [\begin{matrix} D_{n} \\ 0 \end{matrix}] \end{matrix}] . \end{matrix},$

Здесь, объект и выходные возмущения повторно упорядочиваются так, чтобы измеренные выходные параметры предшествовали неизмеренным выходным параметрам.

Оценка состояния

В целом состояния контроллера не измерены и должны быть оценены. По умолчанию диспетчер использует установившийся Фильтр Калмана, который выводит от наблюдателя состояния. (См. Наблюдателя состояния.)

В начале k th интервал управления, состояние контроллера оценивается со следующими шагами:

Получите следующие данные:
- _xc (k |k–1) — Контроллер утверждает оценку от предыдущего интервала управления, k –1
- ^uact (k –1) — Переменная Manipulated (MV), на самом деле используемая на объекте от k –1 к k (принял постоянный),
- ^uopt (k –1) — Оптимальный мВ, рекомендуемый MPC и принятый, чтобы использоваться на объекте от k –1 к k
- v (k) — Текущие измеренные воздействия
- _ym _(k) — Текущий измеренный объект выходные параметры
- _Bu, _Bv — Столбцы параметра наблюдателя B, соответствующий u (k) и v (k) входные параметры
- _Cm — Строки параметра наблюдателя C соответствие измеренному объекту выходные параметры
- _Dmv — Строки и столбцы параметра наблюдателя D, соответствующий измеренному объекту выходные параметры и измеренные входные параметры воздействия
- L, M — Матрицы усиления Константа Кальмана
Сигналы ввода и вывода объекта масштабируются, чтобы быть безразмерными до использования в вычислениях.
Пересмотрите _xc (k |k–1), когда ^uact (k –1) и ^uopt (k –1) будет отличаться:
$x_{c}^{r e v} (k | k - 1) = x_{c} (k | k - 1) + B_{u} [u^{a c t} (k - 1) - u^{o p t} (k - 1)] .$
Вычислите инновации:
$e (k) = y_{m} (k) - [C_{m} x_{c}^{r e v} (k | k - 1) + D_{m v} v (k)] .$
Обновите оценку состояния контроллера, чтобы составлять последние измерения.

$x_{c} (k | k) = x_{c}^{r e v} (k | k - 1) + M e (k) .$
Затем программное обеспечение использует оценку текущего состояния _xc (k |k), чтобы решить квадратичную программу в интервале k. Решением является ^uopt (k), рекомендуемое MPC управляемое значение переменных, которое будет использоваться между интервалами управления k и k +1.
Наконец, программное обеспечение готовится к следующему интервалу управления, принимающему, что неизвестные входные параметры, _wid (k), _wod (k) и _wn (k) принимают свое среднее значение (нуль) между временами k и k +1. Программное обеспечение предсказывает влияние известных входных параметров и инноваций можно следующим образом:
$x_{c} (k + 1 | k) = A x_{c}^{r e v} (k | k - 1) + B_{u} u^{o p t} (k) + B_{v} v (k) + L e (k) .$

Встроенный установившийся Кальман получает вычисление

Программное обеспечение Model Predictive Control Toolbox™ использует команду kalman, чтобы вычислить, Оценка состояния фильтра Калмана получает L и M. Следующие предположения применяются:

Параметры наблюдателя состояния A, B, C, D независим от времени.
Диспетчер утверждает, _xc, обнаруживаемы. (В противном случае или если наблюдатель численно близко к необнаружительной способности, сбоям вычисления усиления Кальмана, генерируя сообщение об ошибке.)
Стохастические входные параметры _wid (k), _wod (k) и _wn (k) являются независимым белым шумом, каждым с нулевым средним значением и единичной ковариацией.
Дополнительный белый шумовой _wu (k) и _wv (k) с теми же характеристиками добавляет к безразмерному u (k) и v (k) входные параметры соответственно. Это улучшает производительность средства оценки в определенных случаях, такой как тогда, когда модель объекта управления является нестабильным разомкнутым циклом.

Без потери общности, устанавливает u (k), и v (k) вводит, чтобы обнулить. Эффект стохастических входных параметров на состояниях контроллера и измеренном объекте выходные параметры:

$\begin{matrix} x_{c} (k + 1) = A x_{c} (k) + B w (k) \\ y_{m} (k) = C_{m} x_{c} (k) + D_{m} w (k) . \end{matrix}$

Здесь,

$w^{T} (k) = [\begin{matrix} w_{u}^{T} (k) & w_{v}^{T} (k) & \begin{matrix} \begin{matrix} w_{i d}^{T} (k) & w_{o d}^{T} (k) \end{matrix} & w_{n}^{T} (k) \end{matrix} \end{matrix}] .$

Входные параметры к команде kalman являются параметрами наблюдателя состояния A, _Cm и следующие ковариационные матрицы:

$\begin{matrix} Q = E {B w w^{T} B^{T}} = B B^{T} \\ R = E {D_{m} w w^{T} D_{m}^{T}} = D_{m} D_{m}^{T} \\ N = E {B w w^{T} D_{m}^{T}} = B D_{m}^{T} . \end{matrix}$

Здесь, E {...} Обозначает ожидание.

Прогноз выходной переменной

Образцовое Прогнозирующее Управление требует прогноза бесшумного будущего объекта выходные параметры, используемые в оптимизации. Это - ключевое приложение наблюдателя состояния (см. Наблюдателя состояния).

В интервале управления k необходимые данные следующие:

p Горизонт прогноза (количество интервалов управления, которое больше, чем или равно 1),
_xc (k |k) — оценки состояния Контроллера (см. Оценку состояния),
v (k) — Текущее измеренное воздействие вводит (MDS)
v (k +i|k) — Спроектированный будущий MDS, где i =1:p–1. Если вы не используете предварительный просмотр MD, то v (k +i|k) = v (k).
A, _Bu, _Bv, C, _Dv — Константы наблюдателя состояния, где _Bu, _Bv и _Dv обозначают столбцы B и соответствия матриц D входным параметрам u и v. _Du является нулевой матрицей ни из-за какого прямого сквозного соединения

Прогнозы принимают, что неизвестные белые шумовые входные параметры являются нулем (их ожидание). Кроме того, предсказанный объект выходные параметры должен быть бесшумным. Таким образом все условия, включающие состояния шума измерения, исчезают из уравнений наблюдателя состояния. Это эквивалентно обнулению последних элементов _nxn _xc (k |k).

Данный вышеупомянутые данные и упрощения, для первого шага наблюдатель состояния предсказывает:

$x_{c} (k + 1 | k) = A x_{c} (k | k) + B_{u} u (k | k) + B_{v} v (k) .$

Продолжая для последовательных шагов, i = 2:p, наблюдатель состояния предсказывает:

$x_{c} (k + i | k) = A x_{c} (k + i - 1 | k) + B_{u} u (k + i - 1 | k) + B_{v} v (k + i - 1 | k) .$

На любом шаге, i = 1:p, предсказанный бесшумный объект выходные параметры:

$y (k + i | k) = C x_{c} (k + i | k) + D_{v} v (k + i | k) .$

Все эти уравнения используют безразмерные переменные ввода и вывода объекта. Смотрите Задают Масштабные коэффициенты. Уравнения также принимают нулевые смещения. Включение ненулевых смещений является прямым.

Для более быстрых вычислений диспетчер MPC использует альтернативную форму вышеупомянутых уравнений, в которых постоянные условия вычисляются и хранятся во время инициализации контроллера. См. Матрицы QP.

Смотрите также

kalman

Документация