(Не рекомендуемый), Собирают матрицы конечного элемента и решают эллиптический УЧП
assempde не рекомендуется. Используйте solvepde вместо этого.
u = assempde(model,c,a,f)u = assempde(b,p,e,t,c,a,f)[Kc,Fc,B,ud]
= assempde(___)[Ks,Fs]
= assempde(___)[K,M,F,Q,G,H,R]
= assempde(___)[K,M,F,Q,G,H,R]
= assempde(___,[],sdl)u = assempde(K,M,F,Q,G,H,R)[Ks,Fs]
= assempde(K,M,F,Q,G,H,R)[Kc,Fc,B,ud]
= assempde(K,M,F,Q,G,H,R)[, для любого из предыдущих входных синтаксисов, собирает матрицы конечного элемента с помощью формы reduced linear system, которая устраняет любые граничные условия Дирихле из системы линейных уравнений. Можно вычислить решение Kc,Fc,B,ud]
= assempde(___)u в точках узла командой u = B*(Kc\Fc) + ud. Смотрите Уменьшаемую Линейную систему.
[ собирает матрицы конечного элемента, которые представляют любые граничные условия Дирихле с помощью приближения stiff-spring. Можно вычислить решение Ks,Fs]
= assempde(___)u в точках узла командой u = Ks\Fs. Смотрите Приближение жесткого Spring.
Решите эллиптический УЧП на L-образной области.
Создайте скалярную модель PDE. Включите геометрию L-образной области.
model = createpde; geometryFromEdges(model,@lshapeg);
Примените нуль граничные условия Дирихле ко всем ребрам.
applyBoundaryCondition(model,'Edge',1:model.Geometry.NumEdges,'u',0);
Сгенерируйте mesh конечного элемента.
generateMesh(model,'GeometricOrder','linear');
Решите УЧП с параметрами c = 1, a = 0 и f = 5.
c = 1; a = 0; f = 5; u = assempde(model,c,a,f);
Постройте решение.
pdeplot(model,'XYData',u)
Решите 3-D эллиптический УЧП с помощью модели PDE.
Создайте контейнер модели PDE, импортируйте 3-D описание геометрии и просмотрите геометрию.
model = createpde; importGeometry(model,'Block.stl'); pdegplot(model,'FaceLabels','on','FaceAlpha',0.5)

Установите нуль условия Дирихле на поверхностях 1 - 4 (ребра). Установите Неймановы условия с g = -1 на поверхности 6 и g = 1 на поверхности 5.
applyBoundaryCondition(model,'Face',1:4,'u',0); applyBoundaryCondition(model,'Face',6,'g',-1); applyBoundaryCondition(model,'Face',5,'g',1);
Установите коэффициенты c = 1, a = 0 и f = 0.1.
c = 1; a = 0; f = 0.1;
Создайте mesh и решите проблему.
generateMesh(model); u = assempde(model,c,a,f);
Постройте решение на поверхности.
pdeplot3D(model,'ColorMapData',u)
Решите 2D УЧП с помощью более старого синтаксиса для mesh.
Создайте круговую геометрию.
g = @circleg;
Установите нуль граничные условия Дирихле.
b = @circleb1;
Создайте mesh для геометрии.
[p,e,t] = initmesh(g);
Решите УЧП с параметрами c = 1, a = 0 и f = sin(x).
c = 1;
a = 0;
f = 'sin(x)';
u = assempde(b,p,e,t,c,a,f);Постройте решение.
pdeplot(p,e,t,'XYData',u)
Получите матрицы конечного элемента, которые представляют проблему с помощью уменьшаемого представления линейной алгебры граничных условий Дирихле.
Создайте скалярную модель PDE. Импортируйте простую 3-D геометрию.
model = createpde;
importGeometry(model,'Block.stl');Установите нуль граничные условия Дирихле на всех поверхностях геометрии.
applyBoundaryCondition(model,'dirichlet','Face',1:model.Geometry.NumFaces,'u',0);
Сгенерируйте mesh для геометрии.
generateMesh(model);
Получите матрицы конечного элемента K, F, B и ud, которые представляют уравнение с параметрами , , и .
c = 1;
a = 0;
f = 'log(1+x+y./(1+z))';
[K,F,B,ud] = assempde(model,c,a,f);Можно получить решение u УЧП в узлах mesh путем выполнения команды
u = B*(K\F) + ud;
Обычно это решение немного более точно, чем жестко-пружинное решение, как вычислено в следующем примере.
Получите жестко-пружинное приближение матриц конечного элемента.
Создайте скалярную модель PDE. Импортируйте простую 3-D геометрию.
model = createpde;
importGeometry(model,'Block.stl');Установите нуль граничные условия Дирихле на всех поверхностях геометрии.
applyBoundaryCondition(model,'Face',1:model.Geometry.NumFaces,'u',0);
Сгенерируйте mesh для геометрии.
generateMesh(model);
Получите матрицы конечного элемента Ks и Fs, которые представляют уравнение с параметрами , , и .
c = 1;
a = 0;
f = 'log(1+x+y./(1+z))';
[Ks,Fs] = assempde(model,c,a,f);Можно получить решение u УЧП в узлах mesh путем выполнения команды
u = Ks\Fs;
Обычно это решение немного менее точно, чем уменьшаемое решение для линейной алгебры, как вычислено в предыдущем примере.
Получите полный набор матриц конечного элемента для эллиптической проблемы.
Импортируйте геометрию и настройте эллиптическую проблему с граничными условиями Дирихле. Геометрия Torus.stl имеет только одну поверхность, таким образом, вы должны установить только одно граничное условие.
model = createpde(); importGeometry(model,'Torus.stl'); applyBoundaryCondition(model,'face',1,'u',0); c = 1; a = 0; f = 1; generateMesh(model);
Создайте матрицы конечного элемента, которые представляют эту проблему.
[K,M,F,Q,G,H,R] = assempde(model,c,a,f);
Большинство получившихся матриц довольно разреженно. G, M, Q и R являются всеми нулевыми разреженными матрицами.
howsparse = @(x)nnz(x)/numel(x); disp(['Maximum fraction of nonzero entries in K or H is ',... num2str(max(howsparse(K),howsparse(H)))])
Maximum fraction of nonzero entries in K or H is 0.002006
Чтобы найти решение УЧП, вызовите assempde снова.
u = assempde(K,M,F,Q,G,H,R);
model — PDEPDEModelМодель PDE, заданная как объект PDEModel.
Пример: model = createpde
c Коэффициент УЧПКоэффициент УЧП, заданный как скаляр, матрица, вектор символов, символьный массив, представляет в виде строки скаляр, вектор строки или коэффициентную функцию. c представляет коэффициент c в скалярном УЧП
или в системе УЧП
Вы можете specifyc в различных способах, детализированных в c Коэффициенте для Систем. См. также Задают Скалярные Коэффициенты УЧП в символьной Форме, Задают 2D Скалярные Коэффициенты в Функциональной Форме и Задают 3-D Коэффициенты УЧП в Функциональной Форме.
Пример: 'cosh(x+y.^2)'
Типы данных: double | char | string | function_handle
Поддержка комплексного числа: Да
a Коэффициент УЧПКоэффициент УЧП, заданный как скаляр, матрица, вектор символов, символьный массив, представляет в виде строки скаляр, вектор строки или коэффициентную функцию. a представляет коэффициент a в скалярном УЧП
или в системе УЧП
Вы можете specifya в различных способах, детализированных в a или d Коэффициенте для Систем. См. также Задают Скалярные Коэффициенты УЧП в символьной Форме, Задают 2D Скалярные Коэффициенты в Функциональной Форме и Задают 3-D Коэффициенты УЧП в Функциональной Форме.
Пример: 2*eye(3)
Типы данных: double | char | string | function_handle
Поддержка комплексного числа: Да
f Коэффициент УЧПКоэффициент УЧП, заданный как скаляр, матрица, вектор символов, символьный массив, представляет в виде строки скаляр, вектор строки или коэффициентную функцию. f представляет коэффициент f в скалярном УЧП
или в системе УЧП
Вы можете specifyf в различных способах, детализированных в f Коэффициенте для Систем. См. также Задают Скалярные Коэффициенты УЧП в символьной Форме, Задают 2D Скалярные Коэффициенты в Функциональной Форме и Задают 3-D Коэффициенты УЧП в Функциональной Форме.
Пример: char('sin(x)';'cos(y)';'tan(z)')
Типы данных: double | char | string | function_handle
Поддержка комплексного числа: Да
b Граничные условияГраничные условия, заданные как граничная матрица или массив данных граничных условий. Передайте массив данных граничных условий как указатель на функцию или как имя файла.
Граничная матрица обычно является экспортом из приложения PDE Modeler. Для получения дополнительной информации структуры этой матрицы, смотрите Граничную матрицу для 2D Геометрии.
Массив данных граничных условий является файлом, который вы записываете в синтаксисе, заданном в Граничных условиях путем Записи Функций.
Пример: b = 'circleb1', b = "circleb1" или b = @circleb1
Типы данных: double | char | string | function_handle
p Поймайте в сети точкиПоймайте в сети точки, заданные как 2 Np матрицей точек, где Np является числом точек в mesh. Для описания (p, e, t) матрицы, смотрите Данные о Mesh.
Как правило, вы используете p, e и данные t, экспортированные из приложения PDE Modeler или сгенерированные initmesh или refinemesh.
Пример: [p,e,t] = initmesh(gd)
Типы данных: double
e Поймайте в сети ребраПоймайте в сети ребра, заданные как 7-by-Ne матрица ребер, где Ne является количеством ребер в mesh. Для описания (p, e, t) матрицы, смотрите Данные о Mesh.
Как правило, вы используете p, e и данные t, экспортированные из приложения PDE Modeler или сгенерированные initmesh или refinemesh.
Пример: [p,e,t] = initmesh(gd)
Типы данных: double
t Поймайте в сети треугольникиПоймайте в сети треугольники, заданные как 4-by-Nt матрица треугольников, где Nt является количеством треугольников в mesh. Для описания (p, e, t) матрицы, смотрите Данные о Mesh.
Как правило, вы используете p, e и данные t, экспортированные из приложения PDE Modeler или сгенерированные initmesh или refinemesh.
Пример: [p,e,t] = initmesh(gd)
Типы данных: double
K Матрица жесткостиМатрица жесткости, заданная как разреженная матрица или полная матрица. Обычно вы получаете K от предыдущего вызова до assema или assempde. Для значения матрицы жесткости смотрите Эллиптические уравнения.
Пример: [K,M,F,Q,G,H,R] = assempde(model,c,a,f)
Типы данных: double
Поддержка комплексного числа: Да
M Большая матрицаБольшая матрица, заданная как разреженная матрица или полная матрица. Обычно вы получаете M от предыдущего вызова до assema или assempde. Для значения большой матрицы смотрите Эллиптические уравнения.
Пример: [K,M,F,Q,G,H,R] = assempde(model,c,a,f)
Типы данных: double
Поддержка комплексного числа: Да
F Конечный элемент представление fКонечный элемент представление f, заданное как вектор. Обычно вы получаете F от предыдущего вызова до assema или assempde. Для значения этого представления смотрите Эллиптические уравнения.
Пример: [K,M,F,Q,G,H,R] = assempde(model,c,a,f)
Типы данных: double
Поддержка комплексного числа: Да
Q Нейманова матрица граничного условияНейманова матрица граничного условия, заданная как разреженная матрица или полная матрица. Обычно вы получаете Q от предыдущего вызова до assemb или assempde. Для значения этой матрицы смотрите Эллиптические уравнения.
Пример: [K,M,F,Q,G,H,R] = assempde(model,c,a,f)
Типы данных: double
Поддержка комплексного числа: Да
G Нейманов вектор граничного условияНейманов вектор граничного условия, заданный как разреженный векторный или полный вектор. Обычно вы получаете G от предыдущего вызова до assemb или assempde. Для значения этого вектора смотрите Эллиптические уравнения.
Пример: [K,M,F,Q,G,H,R] = assempde(model,c,a,f)
Типы данных: double
Поддержка комплексного числа: Да
H Матрица граничного условия ДирихлеR Вектор граничного условия Дирихлеsdl — Метки субдоменаМетки субдомена, заданные как вектор положительных целых чисел. Для 2D геометрии только. Просмотрите метки субдомена в своей геометрии с помощью команды
pdegplot(g,'SubdomainLabels','on')
Пример: sdl = [1,3:5];
Типы данных: double
u Решение для УЧПРешение для УЧП, возвращенное как вектор.
Если УЧП является скаляром, означая только одно уравнение, то u является вектор-столбцом, представляющим решение u в каждом узле в mesh. u(i) является решением в i th столбец model.Mesh.Nodes или i th столбец p.
Если УЧП является системой N> 1 уравнение, то u является вектор-столбцом с N *Np элементы, где Np является количеством узлов в mesh. Первые элементы Np u представляют решение уравнения 1, затем следующие элементы Np представляют решение уравнения 2 и т.д.
Чтобы получить решение в произвольной точке в геометрии, используйте pdeInterpolant.
Чтобы построить решение, используйте pdeplot для 2D геометрии или см. График 3-D Решения и Их Градиенты.
Kc — Матрица жесткостиМатрица жесткости, возвращенная как разреженная матрица. Смотрите Эллиптические уравнения.
u1 = Kc\Fc возвращает решение на точках не-Дирихле. Получить решение u в узлах mesh,
u = B*(Kc\Fc) + ud
Обычно Kc, Fc, B и ud делают более медленное, но более точное решение, чем Ks и Fs.
ФК Вектор загрузкиВектор загрузки, возвращенный как вектор. Смотрите Эллиптические уравнения.
u = B*(Kc\Fc) + ud
Обычно Kc, Fc, B и ud делают более медленное, но более точное решение, чем Ks и Fs.
B Дирихле nullspaceДирихле nullspace, возвращенный как разреженная матрица. См. Алгоритмы.
u = B*(Kc\Fc) + ud
Обычно Kc, Fc, B и ud делают более медленное, но более точное решение, чем Ks и Fs.
ud — Вектор ДирихлеВектор Дирихле, возвращенный как вектор. См. Алгоритмы.
u = B*(Kc\Fc) + ud
Обычно Kc, Fc, B и ud делают более медленное, но более точное решение, чем Ks и Fs.
Ks — Матричное соответствие жесткости жестко-пружинному приближению для граничного условия ДирихлеМатрица конечного элемента для жестко-пружинного приближения, возвращенного как разреженная матрица. См. Алгоритмы.
Получить решение u в узлах mesh,
u = Ks\Fs.
Обычно Ks и Fs делают более быстрое, но менее точное решение, чем Kc, Fc, B и ud.
Fs — Загрузите вектор, соответствующий жестко-пружинному приближению для граничного условия ДирихлеЗагрузите вектор, соответствующий жестко-пружинному приближению для граничного условия Дирихле, возвращенного как вектор. См. Алгоритмы.
Получить решение u в узлах mesh,
u = Ks\Fs.
Обычно Ks и Fs делают более быстрое, но менее точное решение, чем Kc, Fc, B и ud.
K Матрица жесткостиМатрица жесткости, возвращенная как разреженная матрица. Смотрите Эллиптические уравнения.
K представляет одну только матрицу жесткости, в отличие от Kc или Ks, которые являются матрицами жесткости, объединенными с другими условиями, чтобы включить мгновенное решение УЧП.
Как правило, вы используете K в последующем вызове решателя, такого как assempde или hyperbolic.
M Большая матрицаБольшая матрица. возвращенный как разреженная матрица. Смотрите Эллиптические уравнения.
Как правило, вы используете M в последующем вызове решателя, такого как assempde или hyperbolic.
F Вектор загрузкиВектор загрузки, возвращенный как вектор. Смотрите Эллиптические уравнения.
F представляет один только вектор загрузки, в отличие от Fc или Fs, которые являются векторами загрузки, объединенными с другими условиями, чтобы включить мгновенное решение УЧП.
Как правило, вы используете F в последующем вызове решателя, такого как assempde или hyperbolic.
Q Нейманова матрица граничного условияНейманова матрица граничного условия, возвращенная как разреженная матрица. Смотрите Эллиптические уравнения.
Как правило, вы используете Q в последующем вызове решателя, такого как assempde или hyperbolic.
G Нейманов вектор граничного условияНейманов вектор граничного условия, возвращенный как разреженный вектор. Смотрите Эллиптические уравнения.
Как правило, вы используете G в последующем вызове решателя, такого как assempde или hyperbolic.
H Матрица ДирихлеМатрица Дирихле, возвращенная как разреженная матрица. См. Алгоритмы.
Как правило, вы используете H в последующем вызове решателя, такого как assempde или hyperbolic.
R Вектор ДирихлеВектор Дирихле, возвращенный как разреженный вектор. См. Алгоритмы.
Как правило, вы используете R в последующем вызове решателя, такого как assempde или hyperbolic.
Эта форма матриц конечного элемента устраняет условия Дирихле из проблемы с помощью подхода линейной алгебры. Матрицы конечного элемента уменьшают до решения u = B*(Kc\Fc) + ud, где B охватывает пустой пробел столбцов H (матрица условия Дирихле представление hu = r). R является вектором условия Дирихле для Hu = R. ud является вектором решений для граничного условия для условий Дирихле. u1 = Kc\Fc возвращает решение на точках не-Дирихле.
Смотрите, что Системы УЧП для получения дополнительной информации о подходе раньше устраняли условия Дирихле.
Эта форма матриц конечного элемента преобразовывает граничные условия Дирихле в Неймановы граничные условия с помощью жестко-пружинного приближения. Используя это приближение, assempde возвращает матричный Ks и векторный Fs, которые представляют объединенные матрицы конечного элемента. Приближенным решением u является u = Ks\Fs.
Смотрите Эллиптические уравнения. Для получения дополнительной информации жестко-пружинного приближения, смотрите Системы УЧП.
Partial Differential Equation Toolbox™ решает уравнения формы
Когда m и коэффициенты d 0, это уменьшает до
который документация вызывает уравнение elliptic, является ли уравнение эллиптическим в математическом смысле. Уравнение содержит в Ω, где Ω является ограниченной областью в два или три измерения. c, a, f и неизвестное решение u являются комплексными функциями, заданными на Ω. c может также быть матричной функцией 2 на 2 на Ω. Граничные условия задают комбинацию u и его производной по нормали на контуре:
Дирихле: hu = r на контуре ∂ Ω.
Обобщенный Нейман: · (c ∇u) + qu = g на ∂ Ω.
Смешанный: Только применимый к системам. Комбинация Дирихле и обобщенного Неймана.
исходящий нормальный модуль. g, q, h и r являются функциями, определяемыми на ∂ Ω.
Наша номенклатура отклоняется немного от традиции для теории потенциала, где Нейманово условие обычно относится к случаю, q = 0 и наш Нейман был бы назван смешанным условием. В некоторых контекстах обобщенные Неймановы граничные условия также упоминаются как граничные условия Робина. В вариационном исчислении условия Дирихле также называются существенными граничными условиями и ограничивают испытательный пробел. Неймановы условия также называются естественными условиями и возникают по мере необходимости условия для решения. Вариационная форма уравнения Partial Differential Equation Toolbox с Неймановыми условиями приведена ниже.
Приближенное решение эллиптического УЧП найдено на трех шагах:
Опишите геометрию области Ω и граничные условия. Для 2D геометрии создайте геометрию с помощью приложения PDE Modeler или через файлы MATLAB®. Для 3-D геометрии импортируйте геометрию в формате файла STL. Смотрите Геометрию, Импорт Файла STL и Граничные условия.
Создайте треугольную mesh на области Ω. Программное обеспечение имеет генерацию mesh и перерабатывающие мощности mesh. Mesh описана тремя матрицами фиксированного формата, которые содержат информацию о точках mesh, граничных сегментах и элементах.
Дискретизируйте УЧП и граничные условия, чтобы получить линейную систему Ku = F. Неизвестный векторный u содержит значения приближенного решения в точках mesh, матричный K собран от коэффициентов c, a, h, и q и правая сторона, F содержит, по существу, средние значения f вокруг каждой точки mesh и вкладов от g. Однажды матрицы K and F собран, у вас есть целая среда MATLAB в вашем распоряжении, чтобы решить линейную систему и дальнейший процесс решение.
Более тщательно продуманные приложения используют метод конечных элементов (FEM) определенная информация, возвращенная различными функциями программного обеспечения. Поэтому мы быстро обобщаем теорию и метод решателей FEM, чтобы позволить усовершенствованным приложениям полностью использовать вычисленные количества.
FEM может быть получен в итоге в следующем предложении: Спроектируйте слабую форму дифференциального уравнения на конечномерное функциональное пространство. Остальная часть этого раздела имеет дело с объяснением предыдущего оператора.
Мы запускаем со слабой формы дифференциального уравнения. Не ограничивая общность, мы принимаем обобщенные Неймановы условия на целом контуре, поскольку условия Дирихле могут быть аппроксимированы обобщенными Неймановыми условиями. В простом случае единичной матрицы h установка g = qr и затем разрешение q → ∞ приводят к условию Дирихле, потому что деление с очень большим q отменяет условия производной по нормали. Фактическая реализация отличается, поскольку предыдущая процедура может создать проблемы создания условий. Смешанное граничное условие системного случая требует более сложного лечения, описанного в Системах УЧП.
Примите, что u является решением дифференциального уравнения. Умножьте уравнение с произвольной тестовой функцией v и объединяйтесь на Ω:
Объединяйтесь частями (т.е. используйте формулу Грина) получить
Граничный интеграл может быть заменен граничным условием:
Замените исходную проблему на Находку вы таким образом что
Это уравнение называется вариационной, или слабой, формой дифференциального уравнения. Очевидно, любое решение дифференциального уравнения является также решением вариационной проблемы. Реверс верен в условиях некоторых ограничений на область и на коэффициентные функции. Решение вариационной проблемы также называется слабым решением дифференциального уравнения.
Решение u и тестовые функции v принадлежит некоторому функциональному пространству V. Следующий шаг должен выбрать подпространство Np-dimensional . Предположите, что слабая форма дифференциального уравнения на конечномерное функциональное пространство просто означает запрашивать u и v лечь в вместо V. Решение конечномерной проблемы оказывается элементом это находится самое близкое к слабому решению, когда измерено в энергетической норме. Сходимость гарантируется если пробел склоняется к V как Np →∞. Поскольку дифференциальный оператор линеен, мы требуем, чтобы вариационному уравнению удовлетворили для тестовых функций Np Φi ∊ та форма основание, т.е.
Расширьте u в том же основании элементы
и получите систему уравнений
Используйте следующие обозначения:
и перепишите систему в форме
| (K + M + Q) U = F + G. | (1) |
K, M и Q является Np-by-Np матрицы, и F и G является Np - векторы. K, M и F производятся assema, в то время как Q, G производится assemb. Когда не необходимо отличить K, M, и Q или F и G, мы сворачиваем обозначения к KU = F, которые формируют вывод assempde.
Когда проблема является самопримыкающей и эллиптической в обычном математическом смысле, матричный K + M +, Q становится симметричным и положительным определенный. Много типичных проблем имеют эти характеристики, прежде всего те, которые могут также быть сформулированы как проблемы минимизации. Для случая скалярного уравнения K, M и Q очевидно симметричны. Если c (x) ≥ δ> 0, a (x) ≥ 0 и q (x) ≥ 0 с q (x)> 0 на некоторой части ∂ Ω, то, если U ≠ 0.
UT (K + M + Q) U является энергетической нормой. Существует много вариантов тестовых функциональных пространств. Программное обеспечение использует непрерывные функции, которые линейны на каждом элементе 2D mesh, и линейны или квадратичны на элементах 3-D mesh. Кусочная линейность гарантирует, что интегралы, задающие матрицу жесткости K, существуют. Проекция на не что иное как линейная интерполяция, и оценка решения в элементе сделана только с точки зрения узловых значений. Если mesh однородно усовершенствована, аппроксимирует набор сглаженных функций на Ω.
Подходящее основание для в 2D набор функций “палатки” или “шляпы” ϕ i. Они линейны на каждом элементе и принимают значение 0 во всех узлах xj за исключением xi. Для определения основных функций для 3-D геометрии смотрите Основание Конечного элемента для 3-D. Запрос ϕ i (xi) = 1 урожай очень приятное свойство
Таким образом, путем решения системы FEM мы получаем узловые значения приближенного решения. i ϕ основной функции исчезает на всех элементах, которые не содержат узел xi. Непосредственное следствие - то, что интегралы, появляющиеся в Ki,j, Mi,j, Qi,j, Fi и Gi только, должны быть вычислены на элементах, которые содержат узел x i. Во-вторых, это означает, что Ki,j andMi,j является нулем, если xi и xj не являются вершинами того же элемента, и таким образом K и M являются очень разреженными матрицами. Их разреженная структура зависит от упорядоченного расположения индексов точек mesh.
Интегралы в матрицах FEM вычисляются путем добавления вкладов от каждого элемента до соответствующих записей (т.е. только если соответствующая точка mesh является вершиной элемента). Этот процесс обычно называется, собираясь, отсюда имя функционального assempde.
Собирающиеся стандартные программы сканируют элементы mesh. Для каждого элемента они вычисляют так называемые локальные матрицы и добавляют их компоненты в правильные положения в разреженных матрицах или векторах.
Обсуждение теперь специализируется к треугольным сеткам на 2D. Локальные 3х3 матрицы содержат интегралы, оцененные только на текущем треугольнике. Коэффициенты приняты постоянные на треугольнике, и они оценены только в треугольном барицентре. Интегралы вычисляются, используя правило средней точки. Это приближение оптимально, поскольку оно имеет тот же порядок точности как кусочная линейная интерполяция.
Считайте треугольник данным узлами P 1, P 2, и P 3 как в следующей фигуре.
Локальный треугольник P1P2P3
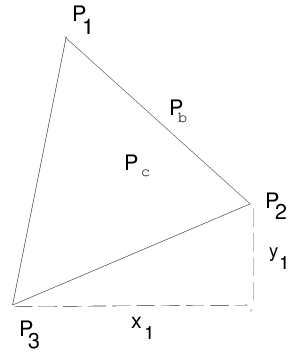
Локальные 3х3 матрицы содержат интегралы, оцененные только на текущем треугольнике. Коэффициенты приняты постоянные на треугольнике, и они оценены только в треугольном барицентре.
Самыми простыми вычислениями является для локальной большой матрицы m:
где Pc является центром массы Δ P 1P2P3, т.е.
Вклад в правую сторону F справедлив
Для локальной матрицы жесткости мы должны оценить градиенты основных функций, которые не исчезают на P 1P2P3. Поскольку основные функции линейны на треугольном P 1P2P3, градиенты являются константами. Обозначьте основные функции ϕ 1, ϕ 2, и ϕ 3 таким образом что ϕ (Pi) = 1. Если P 2 – P 3 = [x 1, y 1] T затем у нас есть это
и после интегрирования (берущий c в качестве постоянной матрицы на треугольнике)
Если две вершины треугольной лжи на контуре ∂ Ω, они способствуют линейным интегралам, сопоставленным к граничным условиям. Если этими двумя граничными точками является P 1 и P 2, то мы имеем
и
где Pb является средней точкой P 1P2.
Для каждого треугольника вершины Pm локального треугольника соответствуют индексам im точек mesh. Вклады отдельного треугольника добавляются к матрицам, таким образом что, например,
Это сделано функциональным assempde. Градиенты и области треугольников вычисляются функциональным pdetrg.
Граничные условия Дирихле обработаны немного отличающимся способом. Они устраняются из линейной системы процедурой, которая приводит к симметричной, уменьшаемой системе. Функциональный assempde может возвратить матрицы K, F, B и ud, таким образом, что решением является u = Bv + ud где Kv = F. u является Np - вектор, и если рангом условий Дирихле является rD, то v имеет Np – компоненты rD.
Подводя итоги, assempde выполняет следующие шаги, чтобы получить решение u к эллиптическому УЧП:
Сгенерируйте матрицы конечного элемента [K, M, F, Q, G, H, R]. Этот шаг эквивалентен вызову assema, чтобы сгенерировать матрицы K, M, и F и также вызов assemb, чтобы сгенерировать матрицы Q, G, H и R.
Сгенерируйте объединенные матрицы конечного элемента [Kc, Fc, B, ud]. Объединенная матрица жесткости для уменьшаемой линейной системы, Kc = K + M + Q. Соответствующим объединенным вектором загрузки является Fc = F + G. Матрица B охватывает пустой пробел столбцов H (матрица условия Дирихле представление hu = r). Вектор R представляет условия Дирихле в Hu = R. Вектор ud представляет решения для граничного условия для условий Дирихле.
Вычислите решение u через
u = B*(Kc\Fc) + ud. | (2) |
assempde использует один из двух алгоритмов для сборки проблемы в объединенную матричную форму конечного элемента. Форма reduced linear system приводит к мгновенному решению через линейную алгебру. Вы выбираете алгоритм количеством выходных параметров. Для уменьшаемой формы линейной системы запросите четыре выходных параметров:
[Kc,Fc,B,ud] = assempde(_) | (3) |
Для stiff-spring approximation запросите два выходных параметров:
[Ks,Fs] = assempde(_) | (4) |
Для получения дополнительной информации смотрите Уменьшаемое Приближение Линейной системы и жесткого Spring.
Программное обеспечение Partial Differential Equation Toolbox может также обработать системы дифференциальных уравнений с частными производными N по области Ω. У нас есть эллиптическая система
параболическая система
гиперболическая система
и система собственного значения
где c является N-by-N-by-D-by-D тензор, и D является размерностями геометрии, 2 или 3.
Для 2D систем, обозначения представляет N-by-1 матрица с (i, 1) - компонент
Для 3-D систем, обозначения представляет N-by-1 матрица с (i, 1) - компонент
Символы a и d обозначают N-by-N матрицы, и f обозначает вектор-столбец длины N.
Элементы cijkl, aij, dij и fi c, a, d, и f хранятся построчные в матрицах MATLAB c, a, d и f. Случай идентичности, диагонали и симметричных матриц обработан как особые случаи. Для тензора cijkl это применяет и к индексам i и к j, и к индексам k и l.
Программное обеспечение Partial Differential Equation Toolbox не проверяет эллиптичность проблемы, и довольно возможно задать систему, которая не является эллиптической в математическом смысле. Предыдущая процедура, которая описывает скалярный случай, применяется к каждому компоненту системы, приводя к симметричной положительной определенной системе уравнений каждый раз, когда дифференциальная система обладает этими характеристиками.
Граничные условия теперь в целом смешаны, т.е. для каждой точки на контуре комбинация Дирихле и обобщили Неймановы условия,
Для 2D систем, обозначения представляет N-by-1 матрица с (i, 1) - компонент
где исходящий вектор нормали контура .
Для 3-D систем, обозначения представляет N-by-1 матрица с (i, 1) - компонент
где исходящее нормальное к контуру
Существует M, условиями Дирихле и h-матрицей является M-by-N, M ≥ 0. Обобщенное Нейманово условие содержит источник , где множители Лагранжа, μ вычисляется таким образом, что условия Дирихле становятся удовлетворенными. В структурной проблеме механики этот термин является точно силой реакции, необходимой, чтобы удовлетворить кинематические ограничения, описанные условиями Дирихле.
Остальная часть этого раздела детализирует обработку условий Дирихле и может быть пропущена на первом чтении.
Программное обеспечение Partial Differential Equation Toolbox поддерживает две реализации условий Дирихле. Самой простой является модель “Stiff Spring”, таким образом названная по имени ее интерпретации в механике твердого тела. Смотрите Эллиптические уравнения для скалярного случая, который эквивалентен диагональной h-матрице. Для общего случая, условий Дирихле
| hu = r | (5) |
аппроксимированы путем добавления термина
к уравнениям KU = F, где L является большим количеством такой как 104 раза представительный размер элементов K.
Когда это число будет увеличено, hu = r будет более точно удовлетворен, но потенциальное плохо создание условий измененных уравнений станет более серьезным.
Второй метод также применим к общим смешанным условиям с недиагональным h, и свободен от плохо создания условий, но более включен в вычислительном отношении. Примите, что существуют узлы Np в mesh. Затем количеством неизвестных является Np N = Nu. Когда граничные условия Дирихле фиксируют некоторые неизвестные, линейная система может соответственно уменьшаться. Это легко сделано путем удаления строк и столбцов, когда значения u даны, но здесь мы должны обработать случай, когда некоторые линейные комбинации компонентов u даны, hu = r. Они собраны в HU = R, где H является M-by-Nu матрица, и R является M - вектор.
С реакцией сила называет систему, становится
| KU +H´ µ = F | (6) |
| HU = R. | (7) |
Ограничения могут быть решены для M U - переменных, остающегося названного V, Nu – вектор M. Пустой пробел H заполнен столбцами B и U = BV +, ud заставляет U удовлетворить условия Дирихле. Перестановка к диагональной блоком форме использует разреженность H, чтобы ускорить следующее вычисление, чтобы найти B численно стабильным способом. µ может быть устранен путем предварительного умножения B´ с тех пор, конструкцией, HB = 0 или B ´H´ = 0. Уменьшаемая система становится
| B´ KBV = B´ F – B ´Kud | (8) |
который симметричен и положительный определенный, если K.
Метод конечных элементов для 3-D геометрии подобен 2D методу, описанному в Эллиптических уравнениях. Основное различие - то, что элементы в 3-D геометрии являются тетраэдрами, что означает, что основные функции отличаются от тех в 2D геометрии.
Удобно сопоставить четырехгранник с каноническим четырехгранником с системой локальной координаты (r, s, t).
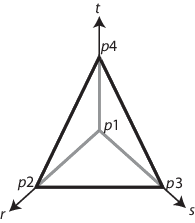
В локальных координатах точка p 1 в (0,0,0), p 2 в (1,0,0), p 3 в (0,1,0), и p 4 в (0,0,1).
Для линейного четырехгранника основные функции
Для квадратичного четырехгранника существуют дополнительные узлы в средних точках ребра.
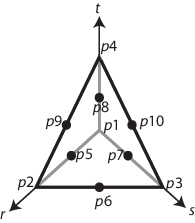
Соответствующие основные функции
Как в 2D случае, 3-D основная функция ϕi принимает значение 0 во всех узлах j, за исключением узла i, где это принимает значение 1.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.