(Не рекомендуемый), Решают гиперболическую проблему УЧП
hyperbolic не рекомендуется. Используйте solvepde вместо этого.
Гиперболический решатель уравнения
Решает проблемы УЧП типа
на 2D или 3-D области Ω, или системная проблема УЧП
Переменные c, a, f и d могут зависеть от положения, время и решение u и его градиент.
u = hyperbolic(u0,ut0,tlist,model,c,a,f,d)u = hyperbolic(u0,ut0,tlist,b,p,e,t,c,a,f,d)u = hyperbolic(u0,ut0,tlist,Kc,Fc,B,ud,M)u = hyperbolic(___,rtol)u =
hyperbolic(___,rtol,atol)u = hyperbolic(u0,ut0,tlist,Kc,Fc,B,ud,M,___,'DampingMatrix',D)u = hyperbolic(___,'Stats','off')u = hyperbolic(u0,ut0,tlist,model,c,a,f,d)
на 2D или 3-D области Ω, или системная проблема УЧП
с геометрией, mesh и граничными условиями, заданными в model, с начальным значением u0 и начальная производная относительно времени ut0. Переменные c, a, f и d в уравнении соответствуют функциональным коэффициентам c, a, f и d соответственно.
u = hyperbolic(___,'Stats','off')
Решите уравнение волны
на квадратной области, заданной squareg.
Создайте модель PDE и импортируйте геометрию.
model = createpde; geometryFromEdges(model,@squareg); pdegplot(model,'EdgeLabels','on') ylim([-1.1,1.1]) axis equal

Установите граничные условия Дирихле для , и Неймановы граничные условия
для . (Нейманово граничное условие является условием по умолчанию, таким образом, вторая спецификация избыточна.)
applyBoundaryCondition(model,'dirichlet','Edge',[2,4],'u',0); applyBoundaryCondition(model,'neumann','Edge',[1,3],'g',0);
Установите начальные условия
u0 = 'atan(cos(pi/2*x))'; ut0 = '3*sin(pi*x).*exp(cos(pi*y))';
Установите времена решения.
tlist = linspace(0,5,31);
Дайте коэффициенты для проблемы.
c = 1; a = 0; f = 0; d = 1;
Сгенерируйте mesh и решите УЧП.
generateMesh(model,'GeometricOrder','linear','Hmax',0.1); u1 = hyperbolic(u0,ut0,tlist,model,c,a,f,d);
462 successful steps 51 failed attempts 1028 function evaluations 1 partial derivatives 135 LU decompositions 1027 solutions of linear systems
Постройте решение в первые и последние времена.
figure
pdeplot(model,'XYData',u1(:,1))
figure
pdeplot(model,'XYData',u1(:,end))
Для версии этого примера с анимацией смотрите уравнение Волны на Квадратной Области.
Решите уравнение волны
на квадратной области, заданной squareg, с помощью функции геометрии, чтобы задать геометрию, граничная функция, чтобы задать граничные условия, и с помощью initmesh, чтобы создать mesh конечного элемента.
Задайте геометрию как @squareg и постройте геометрию.
g = @squareg; pdegplot(g,'EdgeLabels','on') ylim([-1.1,1.1]) axis equal

Установите граничные условия Дирихле для , и Неймановы граничные условия
для . (Нейманово граничное условие является условием по умолчанию, таким образом, вторая спецификация избыточна.)
Функция squareb3 задает эти граничные условия.
b = @squareb3;
Установите начальные условия
u0 = 'atan(cos(pi/2*x))'; ut0 = '3*sin(pi*x).*exp(cos(pi*y))';
Установите времена решения.
tlist = linspace(0,5,31);
Дайте коэффициенты для проблемы.
c = 1; a = 0; f = 0; d = 1;
Создайте mesh и решите УЧП.
[p,e,t] = initmesh(g); u = hyperbolic(u0,ut0,tlist,b,p,e,t,c,a,f,d);
462 successful steps 70 failed attempts 1066 function evaluations 1 partial derivatives 156 LU decompositions 1065 solutions of linear systems
Постройте решение в первые и последние времена.
figure
pdeplot(p,e,t,'XYData',u(:,1))
figure
pdeplot(p,e,t,'XYData',u(:,end))
Для версии этого примера с анимацией смотрите уравнение Волны на Квадратной Области.
Решите гиперболическую проблему с помощью матриц конечного элемента.
Создайте модель и импортируйте геометрию BracketWithHole.stl.
model = createpde(); importGeometry(model,'BracketWithHole.stl'); figure pdegplot(model,'FaceLabels','on') view(30,30) title('Bracket with Face Labels')

figure pdegplot(model,'FaceLabels','on') view(-134,-32) title('Bracket with Face Labels, Rear View')

Установите коэффициенты c = 1, a = 0, f = 0.5 и d = 1.
c = 1; a = 0; f = 0.5; d = 1;
Сгенерируйте mesh для модели.
generateMesh(model);
Создайте начальные условия и граничные условия. Граничным условием для задней поверхности является Дирихле со значением 0. Все другие поверхности имеют граничное условие по умолчанию. Начальным условием является u(0) = 0, du/dt(0) = x/2. Дайте начальное условие на производной путем вычисления x, позиционного из каждого узла в xpts и передачи x/2.
applyBoundaryCondition(model,'Face',4,'u',0); u0 = 0; xpts = model.Mesh.Nodes(1,:); ut0 = xpts(:)/2;
Создайте связанные матрицы конечного элемента.
[Kc,Fc,B,ud] = assempde(model,c,a,f); [~,M,~] = assema(model,0,d,f);
Решите УЧП в течение многих времен от 0 до 2.
tlist = linspace(0,5,50); u = hyperbolic(u0,ut0,tlist,Kc,Fc,B,ud,M);
1493 successful steps 70 failed attempts 2956 function evaluations 1 partial derivatives 276 LU decompositions 2955 solutions of linear systems
Просмотрите решение в несколько раз. Масштабируйте все графики иметь тот же цветовой диапазон при помощи команды caxis.
umax = max(max(u)); umin = min(min(u)); subplot(2,2,1) pdeplot3D(model,'ColorMapData',u(:,5)) caxis([umin umax]) title('Time 1/2') subplot(2,2,2) pdeplot3D(model,'ColorMapData',u(:,10)) caxis([umin umax]) title('Time 1') subplot(2,2,3) pdeplot3D(model,'ColorMapData',u(:,15)) caxis([umin umax]) title('Time 3/2') subplot(2,2,4) pdeplot3D(model,'ColorMapData',u(:,20)) caxis([umin umax]) title('Time 2')

Решение, кажется, имеет частоту одной, потому что графики время от времени 1/2 и 3/2 показывают максимальные значения, и те время от времени 1 и 2 показывают минимальные значения.
Решите гиперболическую проблему, которая включает затухание. Необходимо использовать матричную форму конечного элемента, чтобы использовать затухание.
Создайте модель и импортируйте геометрию BracketWithHole.stl.
model = createpde(); importGeometry(model,'BracketWithHole.stl'); figure pdegplot(model,'FaceLabels','on') view(30,30) title('Bracket with Face Labels')

figure pdegplot(model,'FaceLabels','on') view(-134,-32) title('Bracket with Face Labels, Rear View')

Установите коэффициенты c = 1, a = 0, f = 0.5 и d = 1.
c = 1; a = 0; f = 0.5; d = 1;
Сгенерируйте mesh для модели.
generateMesh(model);
Создайте начальные условия и граничные условия. Граничным условием для задней поверхности является Дирихле со значением 0. Все другие поверхности имеют граничное условие по умолчанию. Начальным условием является u(0) = 0, du/dt(0) = x/2. Дайте начальное условие на производной путем вычисления x, позиционного из каждого узла в xpts и передачи x/2.
applyBoundaryCondition(model,'Face',4,'u',0); u0 = 0; xpts = model.Mesh.Nodes(1,:); ut0 = xpts(:)/2;
Создайте связанные матрицы конечного элемента.
[Kc,Fc,B,ud] = assempde(model,c,a,f); [~,M,~] = assema(model,0,d,f);
Используйте матрицу затухания, которая составляет 10% большой матрицы.
Damping = 0.1*M;
Решите УЧП в течение многих времен от 0 до 2.
tlist = linspace(0,5,50);
u = hyperbolic(u0,ut0,tlist,Kc,Fc,B,ud,M,'DampingMatrix',Damping);1441 successful steps 70 failed attempts 2839 function evaluations 1 partial derivatives 288 LU decompositions 2838 solutions of linear systems
Постройте максимальное значение каждый раз. Ослабление колебаний немного как время увеличивается.
plot(max(u)) xlabel('Time') ylabel('Maximum value') title('Maximum of Solution')

u0 — Начальное условиеНачальное условие, заданное как скаляр, вектор узловых значений, вектора символов, символьного массива, представляет в виде строки скаляр или вектор строки. Начальное условие является значением решения u в начальное время, заданное как вектор-столбец значений в узлах. Узлы являются или p в структуре данных [p,e,t] или являются model.Mesh.Nodes. Для получения дополнительной информации смотрите, Решают УЧП с Начальными условиями.
Если начальным условием является постоянный скалярный v, задайте u0 как v.
Если существуют узлы Np в mesh и уравнения N в системе УЧП, задают u0 как вектор-столбец Np *N элементы, где первые элементы Np соответствуют первому компоненту решения u, вторые элементы Np соответствуют второму компоненту решения u и т.д.
Дайте текстовое выражение функции, такой как 'x.^2 + 5*cos(x.*y)'. Если вы имеете систему N > 1 уравнение, даете текстовый массив такой как
char('x.^2 + 5*cos(x.*y)',... 'tanh(x.*y)./(1+z.^2)')
Пример: x.^2+5*cos(y.*x)
Типы данных: double | char | string
Поддержка комплексного числа: Да
ut0 — Начальная производнаяНачальная производная, заданная как вектор, вектор символов, символьный массив, представляет в виде строки скаляр или вектор строки. Начальный градиент является значением производной решения u в начальное время, заданное как вектор значений в узлах. Узлы являются или p в структуре данных [p,e,t] или являются model.Mesh.Nodes. Смотрите Решают УЧП с Начальными условиями.
Если начальная производная является постоянным значением v, задайте u0 как v.
Если существуют узлы Np в mesh и уравнения N в системе УЧП, задают ut0 как вектор Np *N элементы, где первые элементы Np соответствуют первому компоненту решения u, вторые элементы Np соответствуют второму компоненту решения u и т.д.
Дайте текстовое выражение функции, такой как 'x.^2 + 5*cos(x.*y)'. Если у вас есть система N > 1 уравнение, используйте текстовый массив такой как
char('x.^2 + 5*cos(x.*y)',... 'tanh(x.*y)./(1+z.^2)')
Для получения дополнительной информации смотрите, Решают УЧП с Начальными условиями.
Пример: p(1,:).^2+5*cos(p(2,:).*p(1,:))
Типы данных: double | char | string
Поддержка комплексного числа: Да
tlist — Времена решенияВремена решения, заданные как вектор действительных чисел. Решатель возвращает решение УЧП во времена решения.
Пример: 0:0.2:4
Типы данных: double
model — PDEPDEModelМодель PDE, заданная как объект PDEModel.
Пример: model = createpde
c Коэффициент УЧПКоэффициент УЧП, заданный как скаляр, матрица, вектор символов, символьный массив, представляет в виде строки скаляр, вектор строки или коэффициентную функцию. c представляет коэффициент c в скалярном УЧП
или в системе УЧП
Вы можете specifyc в различных способах, детализированных в c Коэффициенте для Систем. См. также Задают Скалярные Коэффициенты УЧП в символьной Форме, Задают 2D Скалярные Коэффициенты в Функциональной Форме и Задают 3-D Коэффициенты УЧП в Функциональной Форме.
Пример: 'cosh(x+y.^2)'
Типы данных: double | char | string | function_handle
Поддержка комплексного числа: Да
a Коэффициент УЧПКоэффициент УЧП, заданный как скаляр, матрица, вектор символов, символьный массив, представляет в виде строки скаляр, вектор строки или коэффициентную функцию. a представляет коэффициент a в скалярном УЧП
или в системе УЧП
Существует большое разнообразие способов задать a, детализированный в a или d Коэффициенте для Систем. См. также Задают Скалярные Коэффициенты УЧП в символьной Форме, Задают 2D Скалярные Коэффициенты в Функциональной Форме и Задают 3-D Коэффициенты УЧП в Функциональной Форме.
Пример: 2*eye(3)
Типы данных: double | char | string | function_handle
Поддержка комплексного числа: Да
f Коэффициент УЧПКоэффициент УЧП, заданный как скаляр, матрица, вектор символов, символьный массив, представляет в виде строки скаляр, вектор строки или коэффициентную функцию. f представляет коэффициент f в скалярном УЧП
или в системе УЧП
Вы можете specifyf в различных способах, детализированных в f Коэффициенте для Систем. См. также Задают Скалярные Коэффициенты УЧП в символьной Форме, Задают 2D Скалярные Коэффициенты в Функциональной Форме и Задают 3-D Коэффициенты УЧП в Функциональной Форме.
Пример: char('sin(x)';'cos(y)';'tan(z)')
Типы данных: double | char | string | function_handle
Поддержка комплексного числа: Да
d Коэффициент УЧПКоэффициент УЧП, заданный как скаляр, матрица, вектор символов, символьный массив, представляет в виде строки скаляр, вектор строки или коэффициентную функцию. d представляет коэффициент d в скалярном УЧП
или в системе УЧП
Вы можете specifyd в различных способах, детализированных в a или d Коэффициенте для Систем. См. также Задают Скалярные Коэффициенты УЧП в символьной Форме, Задают 2D Скалярные Коэффициенты в Функциональной Форме и Задают 3-D Коэффициенты УЧП в Функциональной Форме.
Пример: 2*eye(3)
Типы данных: double | char | string | function_handle
Поддержка комплексного числа: Да
b Граничные условияГраничные условия, заданные как граничная матрица или массив данных граничных условий. Передайте массив данных граничных условий как указатель на функцию или как имя файла.
Граничная матрица обычно является экспортом из приложения PDE Modeler. Для получения дополнительной информации структуры этой матрицы, смотрите Граничную матрицу для 2D Геометрии.
Массив данных граничных условий является файлом, который вы записываете в синтаксисе, заданном в Граничных условиях путем Записи Функций.
Пример: b = 'circleb1', b = "circleb1" или b = @circleb1
Типы данных: double | char | string | function_handle
p Поймайте в сети точкиПоймайте в сети точки, заданные как 2 Np матрицей точек, где Np является числом точек в mesh. Для описания (p, e, t) матрицы, смотрите Данные о Mesh.
Как правило, вы используете p, e и данные t, экспортированные из приложения PDE Modeler или сгенерированные initmesh или refinemesh.
Пример: [p,e,t] = initmesh(gd)
Типы данных: double
e Поймайте в сети ребраПоймайте в сети ребра, заданные как 7-by-Ne матрица ребер, где Ne является количеством ребер в mesh. Для описания (p, e, t) матрицы, смотрите Данные о Mesh.
Как правило, вы используете p, e и данные t, экспортированные из приложения PDE Modeler или сгенерированные initmesh или refinemesh.
Пример: [p,e,t] = initmesh(gd)
Типы данных: double
t Поймайте в сети треугольникиПоймайте в сети треугольники, заданные как 4-by-Nt матрица треугольников, где Nt является количеством треугольников в mesh. Для описания (p, e, t) матрицы, смотрите Данные о Mesh.
Как правило, вы используете p, e и данные t, экспортированные из приложения PDE Modeler или сгенерированные initmesh или refinemesh.
Пример: [p,e,t] = initmesh(gd)
Типы данных: double
Kc — Матрица жесткостиМатрица жесткости, заданная как разреженная матрица или как полная матрица. Смотрите Эллиптические уравнения. Как правило, Kc является вывод assempde.
ФК Вектор загрузкиВектор загрузки, заданный как вектор. Смотрите Эллиптические уравнения. Как правило, Fc является вывод assempde.
M Большая матрицаБольшая матрица. заданный как разреженная матрица или полная матрица. Смотрите Эллиптические уравнения.
Получить входные матрицы для pdeeig, hyperbolic или parabolic, выполнения и assema и assempde:
[Kc,Fc,B,ud] = assempde(model,c,a,f); [~,M,~] = assema(model,0,d,f);
Создайте матрицу M использование assema с d, не a, в качестве аргумента перед f.
Типы данных: double
Поддержка комплексного числа: Да
rtol — Относительный допуск к решателю ОДУ1e-3 (значение по умолчанию) | положительный действительныйОтносительный допуск к решателю ОДУ, заданному как положительное действительное.
Пример: 2e-4
Типы данных: double
atol — Абсолютный допуск к решателю ОДУ1e-6 (значение по умолчанию) | положительный действительныйАбсолютный допуск к решателю ОДУ, заданному как положительное действительное.
Пример: 2e-7
Типы данных: double
D Затухание матрицыЗатухание матрицы, заданной как матрица. D имеет тот же размер как матрица жесткости Kc или большая матрица M. Когда вы включаете D, hyperbolic решает следующий ОДУ для переменной v:
с начальным условием u0 и начальным производным ut0. Затем hyperbolic возвращает решение u = B*v + ud.
Для примера с помощью D смотрите Динамику Ослабленного Консольного Луча.
Пример: alpha*M + beta*K
Типы данных: double
Поддержка комплексного числа: Да
u Решение для УЧПРешение для УЧП, возвращенное как матрица. Матрицей является Np *N-by-T, где Np является количеством узлов в mesh, N является количеством уравнений в УЧП (N = 1 для скалярного УЧП), и T является номером времен решения, означая длину tlist. Матрица решения имеет следующую структуру.
Первые элементы Np каждого столбца в u представляют решение уравнения 1, затем следующие элементы Np представляют решение уравнения 2 и т.д. Решение u является значением в соответствующем узле в mesh.
Столбец i u представляет решение во время tlist (i).
Чтобы получить решение в произвольной точке в геометрии, используйте pdeInterpolant.
Чтобы построить решение, используйте pdeplot для 2D геометрии или см. График 3-D Решения и Их Градиенты.
Partial Differential Equation Toolbox™ решает уравнения формы
Когда коэффициент d 0, но m не, документация вызывает это уравнение hyperbolic, имеет ли это математически гиперболическую форму.
Используя те же идеи что касается параболического уравнения, hyperbolic реализует числовое решение
для x в Ω, где x представляет 2D или 3-D точку с начальными условиями
для всего x в Ω и обычных граничных условий. В частности, решения уравнения utt - c Δu = 0 являются волнами, перемещающимися со скоростью .
Используя данную сетку Ω, метод строк приводит к системе ОДУ второго порядка
с начальными условиями
после того, как мы устраняем неизвестные, зафиксированные граничными условиями Дирихле. Как прежде, матрица жесткости K и большая матрица M собраны при помощи функционального assempde от проблем
| – ∇ · (c ∇u) + au = f и – ∇ · (0∇u) + mu = 0. | (1) |
hyperbolic внутренне вызывает assema, assemb и assempde, чтобы создать матрицы конечного элемента, соответствующие проблеме. Это вызывает ode15s, чтобы решить получившуюся систему обыкновенных дифференциальных уравнений.
Метод конечных элементов для 3-D геометрии подобен 2D методу, описанному в Эллиптических уравнениях. Основное различие - то, что элементы в 3-D геометрии являются тетраэдрами, что означает, что основные функции отличаются от тех в 2D геометрии.
Удобно сопоставить четырехгранник с каноническим четырехгранником с системой локальной координаты (r, s, t).
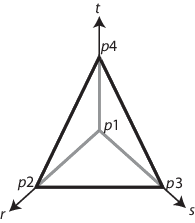
В локальных координатах точка p 1 в (0,0,0), p 2 в (1,0,0), p 3 в (0,1,0), и p 4 в (0,0,1).
Для линейного четырехгранника основные функции
Для квадратичного четырехгранника существуют дополнительные узлы в средних точках ребра.
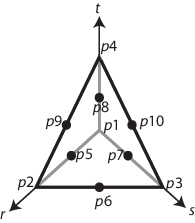
Соответствующие основные функции
Как в 2D случае, 3-D основная функция ϕi принимает значение 0 во всех узлах j, за исключением узла i, где это принимает значение 1.
Программное обеспечение Partial Differential Equation Toolbox может также обработать системы дифференциальных уравнений с частными производными N по области Ω. У нас есть эллиптическая система
параболическая система
гиперболическая система
и система собственного значения
где c является N-by-N-by-D-by-D тензор, и D является размерностями геометрии, 2 или 3.
Для 2D систем, обозначения представляет N-by-1 матрица с (i, 1) - компонент
Для 3-D систем, обозначения представляет N-by-1 матрица с (i, 1) - компонент
Символы a и d обозначают N-by-N матрицы, и f обозначает вектор-столбец длины N.
Элементы cijkl, aij, dij и fi c, a, d, и f хранятся построчные в матрицах MATLAB® c, a, d и f. Случай идентичности, диагонали и симметричных матриц обработан как особые случаи. Для тензора cijkl это применяет и к индексам i и к j, и к индексам k и l.
Программное обеспечение Partial Differential Equation Toolbox не проверяет эллиптичность проблемы, и довольно возможно задать систему, которая не является эллиптической в математическом смысле. Предыдущая процедура, которая описывает скалярный случай, применяется к каждому компоненту системы, приводя к симметричной положительной определенной системе уравнений каждый раз, когда дифференциальная система обладает этими характеристиками.
Граничные условия теперь в целом смешаны, т.е. для каждой точки на контуре комбинация Дирихле и обобщили Неймановы условия,
Для 2D систем, обозначения представляет N-by-1 матрица с (i, 1) - компонент
где исходящий вектор нормали контура .
Для 3-D систем, обозначения представляет N-by-1 матрица с (i, 1) - компонент
где исходящее нормальное к контуру
Существует M, условиями Дирихле и h-матрицей является M-by-N, M ≥ 0. Обобщенное Нейманово условие содержит источник , где множители Лагранжа, μ вычисляется таким образом, что условия Дирихле становятся удовлетворенными. В структурной проблеме механики этот термин является точно силой реакции, необходимой, чтобы удовлетворить кинематические ограничения, описанные условиями Дирихле.
Остальная часть этого раздела детализирует обработку условий Дирихле и может быть пропущена на первом чтении.
Программное обеспечение Partial Differential Equation Toolbox поддерживает две реализации условий Дирихле. Самой простой является модель “Stiff Spring”, таким образом названная по имени ее интерпретации в механике твердого тела. Смотрите Эллиптические уравнения для скалярного случая, который эквивалентен диагональной h-матрице. Для общего случая, условий Дирихле
| hu = r | (2) |
аппроксимированы путем добавления термина
к уравнениям KU = F, где L является большим количеством такой как 104 раза представительный размер элементов K.
Когда это число будет увеличено, hu = r будет более точно удовлетворен, но потенциальное плохо создание условий измененных уравнений станет более серьезным.
Второй метод также применим к общим смешанным условиям с недиагональным h, и свободен от плохо создания условий, но более включен в вычислительном отношении. Примите, что существуют узлы Np в mesh. Затем количеством неизвестных является Np N = Nu. Когда граничные условия Дирихле фиксируют некоторые неизвестные, линейная система может соответственно уменьшаться. Это легко сделано путем удаления строк и столбцов, когда значения u даны, но здесь мы должны обработать случай, когда некоторые линейные комбинации компонентов u даны, hu = r. Они собраны в HU = R, где H является M-by-Nu матрица, и R является M - вектор.
С реакцией сила называет систему, становится
| KU +H´ µ = F | (3) |
| HU = R. | (4) |
Ограничения могут быть решены для M U - переменных, остающегося названного V, Nu – вектор M. Пустой пробел H заполнен столбцами B и U = BV +, ud заставляет U удовлетворить условия Дирихле. Перестановка к диагональной блоком форме использует разреженность H, чтобы ускорить следующее вычисление, чтобы найти B численно стабильным способом. µ может быть устранен путем предварительного умножения B´ с тех пор, конструкцией, HB = 0 или B ´H´ = 0. Уменьшаемая система становится
| B´ KBV = B´ F – B ´Kud | (5) |
который симметричен и положительный определенный, если K.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.