Exponenta Banner

полоса пропускания

Сигналы полосового фильтра

свернуть все на странице

Синтаксис

y = bandpass(x,wpass)
y = bandpass(x,fpass,fs)
y = bandpass(xt,fpass)
y = bandpass(___,Name,Value)
[y,d] = bandpass(___)
bandpass(___)

Описание

y = bandpass(x,wpass) фильтрует входной сигнал x с помощью полосового фильтра с частотным диапазоном полосы пропускания, заданным двухэлементным векторным wpass, и выразил в нормированных единицах рада/выборки π. bandpass использует фильтр минимального заказа с затуханием полосы задерживания 60 дБ и компенсирует задержку, введенную фильтром. Если x является матрицей, функция фильтрует каждый столбец независимо.

пример

y = bandpass(x,fpass,fs) указывает, что x выбирается на уровне герц fs. Двухэлементный векторный fpass задает частотный диапазон полосы пропускания фильтра в герц.

y = bandpass(xt,fpass) полосовые фильтры данные в расписании xt с помощью фильтра с частотным диапазоном полосы пропускания, заданным в герц двухэлементным векторным fpass. Функция независимо фильтрует все переменные в расписании и все столбцы в каждой переменной.

пример

y = bandpass(___,Name,Value) задает дополнительные опции для любого из предыдущих аргументов пары "имя-значение" использования синтаксисов. Можно изменить затухание полосы задерживания, крутизну полосы перехода и тип импульсного ответа фильтра.

пример

[y,d] = bandpass(___) также возвращает объект digitalFilter, d раньше фильтровал вход.

bandpass(___) без выходных аргументов строит входной сигнал и накладывает отфильтрованный сигнал.

Примеры

свернуть все

Скрипт Open Live Script

Создайте сигнал, выбранный на уровне 1 кГц в течение 1 секунды. Сигнал содержит три тона, один на уровне 50 Гц, другого на уровне 150 Гц и одну треть на уровне 250 Гц. Высокочастотные и низкочастотные тоны оба имеют дважды амплитуду промежуточного тона. Сигнал встраивается в Гауссов белый шум отклонения 1/100.

fs = 1e3;
t = 0:1/fs:1;
x = [2 1 2]*sin(2*pi*[50 150 250]'.*t) + randn(size(t))/10;

Полосовой фильтр сигнал удалить низкочастотные и высокочастотные тоны. Задайте частоты полосы пропускания 100 Гц и 200 Гц. Отобразите исходные и отфильтрованные сигналы, и также их спектры.

bandpass(x,[100 200],fs)

Скрипт Open Live Script

Реализуйте основной синтезатор цифровой музыки и используйте его, чтобы проигрывать традиционную песню. Задайте частоту дискретизации 2 кГц. Постройте спектрограмму песни.

fs = 2e3;
t = 0:1/fs:0.3-1/fs;

l = [0 130.81 146.83 164.81 174.61 196.00 220 246.94];
m = [0 261.63 293.66 329.63 349.23 392.00 440 493.88];
h = [0 523.25 587.33 659.25 698.46 783.99 880 987.77];
note = @(f,g) [1 1 1]*sin(2*pi*[l(g) m(g) h(f)]'.*t);

mel = [3 2 1 2 3 3 3 0 2 2 2 0 3 5 5 0 3 2 1 2 3 3 3 3 2 2 3 2 1]+1;
acc = [3 0 5 0 3 0 3 3 2 0 2 2 3 0 5 5 3 0 5 0 3 3 3 0 2 2 3 0 1]+1;

song = [];
for kj = 1:length(mel)
    song = [song note(mel(kj),acc(kj)) zeros(1,0.01*fs)];
end
song = song/(max(abs(song))+0.1);

% To hear, type sound(song,fs)

pspectrum(song,fs,'spectrogram','TimeResolution',0.31, ...
    'OverlapPercent',0,'MinThreshold',-60)

Полосовой фильтр сигнал разделить средний регистр от других двух. Задайте частоты полосы пропускания 230 Гц и 450 Гц. Постройте исходные и отфильтрованные сигналы во временном и частотном диапазоне.

pong = bandpass(song,[230 450],fs);

% To hear, type sound(pong,fs)

bandpass(song,[230 450],fs)

Постройте спектрограмму среднего регистра.

figure
pspectrum(pong,fs,'spectrogram','TimeResolution',0.31, ...
    'OverlapPercent',0,'MinThreshold',-60)

Скрипт Open Live Script

Отфильтруйте белый шум, выбранный на уровне 1 кГц с помощью бесконечного импульсного полосового фильтра ответа с шириной полосы пропускания 100 Гц. Используйте различные значения крутизны. Постройте спектры отфильтрованных сигналов.

fs = 1000;
x = randn(20000,1);

[y1,d1] = bandpass(x,[ 50 150],fs,'ImpulseResponse','iir','Steepness',0.5);
[y2,d2] = bandpass(x,[200 300],fs,'ImpulseResponse','iir','Steepness',0.8);
[y3,d3] = bandpass(x,[350 450],fs,'ImpulseResponse','iir','Steepness',0.95);

pspectrum([y1 y2 y3],fs)
legend('Steepness = 0.5','Steepness = 0.8','Steepness = 0.95', ...
    'Location','south')

Вычислите и постройте частотные характеристики фильтров.

[h1,f] = freqz(d1,1024,fs);
[h2,~] = freqz(d2,1024,fs);
[h3,~] = freqz(d3,1024,fs);

plot(f,mag2db(abs([h1 h2 h3])))
legend('Steepness = 0.5','Steepness = 0.8','Steepness = 0.95', ...
    'Location','south')
ylim([-100 10])

Сделайте фильтры асимметричными путем определения различных значений крутизны в ниже и более высокие частоты полосы пропускания.

[y1,d1] = bandpass(x,[ 50 150],fs,'ImpulseResponse','iir','Steepness',[0.5 0.8]);
[y2,d2] = bandpass(x,[200 300],fs,'ImpulseResponse','iir','Steepness',[0.5 0.8]);
[y3,d3] = bandpass(x,[350 450],fs,'ImpulseResponse','iir','Steepness',[0.5 0.8]);

pspectrum([y1 y2 y3],fs)

Вычислите и постройте частотные характеристики фильтров.

[h1,f] = freqz(d1,1024,fs);
[h2,~] = freqz(d2,1024,fs);
[h3,~] = freqz(d3,1024,fs);

plot(f,mag2db(abs([h1 h2 h3])))
ylim([-100 10])

Входные параметры

свернуть все

Входной сигнал, заданный как вектор или матрица.

Пример: sin(2*pi*(0:127)/16)+randn(1,128)/100 задает шумную синусоиду

Пример: [2 1].*sin(2*pi*(0:127)'./[16 64]) задает двухканальную синусоиду.

Типы данных: single | double
Поддержка комплексного числа: Да

Нормированный частотный диапазон полосы пропускания, заданный как двухэлементный вектор с элементами в интервале (0, 1).

Частотный диапазон полосы пропускания, заданный как двухэлементный вектор с элементами в интервале (0, fs/2).

Частота дискретизации, заданная как положительный действительный скаляр.

Введите расписание. xt должен содержать увеличение, конечные, и равномерно распределенные времена строки типа duration в секундах.

Если расписание имеет пропавших без вести или дублирующиеся моменты времени, можно зафиксировать его с помощью советов в Чистом Расписании с Пропавшими без вести, Копией, или Неоднородные Времена (MATLAB).

Пример: timetable(seconds(0:4)',randn(5,1),randn(5,2)) содержит одноканальный случайный сигнал и двухканальный случайный сигнал, выбранный на уровне 1 Гц в течение 4 секунд.

Аргументы в виде пар имя-значение

Укажите необязательные аргументы в виде пар ""имя, значение"", разделенных запятыми. Имя (Name) — это имя аргумента, а значение (Value) — соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: 'ImpulseResponse','iir','StopbandAttenuation',30 фильтрует вход с помощью БИХ-фильтра минимального заказа, который ослабляет на 30 дБ частоты, меньшие, чем fpass(1) и частоты, больше, чем fpass(2).

Тип импульсного ответа фильтра, заданного как пара, разделенная запятой, состоящая из 'ImpulseResponse' и 'fir', 'iir' или 'auto'.

  • 'fir' — Функция разрабатывает минимальный заказ, линейную фазу, фильтр конечного импульсного ответа (FIR). Чтобы компенсировать задержку, функция добавляет к входному сигналу N/2 нули, где N является порядком фильтра. Функция затем фильтрует сигнал и удаляет первый N/2 выборки вывода.

    В этом случае входной сигнал должен быть, по крайней мере, в два раза длиннее, чем фильтром, который соответствует спецификациям.

  • 'iir' — Функция разрабатывает фильтр бесконечного импульсного ответа (IIR) минимального заказа и использует функцию filtfilt, чтобы выполнить фильтрацию нулевой фазы и компенсировать задержку фильтра.

    Если сигнал не по крайней мере в три раза более длинен, чем фильтр, который соответствует спецификациям, функция разрабатывает фильтр с меньшим порядком и таким образом меньшей крутизной.

  • 'auto' Функция разрабатывает КИХ-фильтр минимального заказа, если входной сигнал достаточно длинен, и БИХ-фильтр минимального заказа в противном случае. А именно, функция выполняет эти шаги:

    • Вычислите минимальный заказ, что КИХ-фильтру, должно быть, придется соответствовать спецификациям. Если сигнал является, по крайней мере, в два раза длиннее, чем необходимым порядком фильтра, проектом, и используйте тот фильтр.

    • Если сигнал не достаточно длинен, вычислите минимальный заказ, что БИХ-фильтру, должно быть, придется соответствовать спецификациям. Если сигнал по крайней мере в три раза более длинен, чем необходимый порядок фильтра, проект, и используйте тот фильтр.

    • Если сигнал не достаточно длинен, обрежьте порядок до одной трети длина сигнала и разработайте БИХ-фильтр того порядка. Сокращение по порядку происходит за счет крутизны полосы перехода.

    • Отфильтруйте сигнал и компенсируйте задержку.

Крутизна полосы перехода, заданная как пара, разделенная запятой, состоящая из 'Steepness' и скалярного или двухэлементного вектора с элементами в интервале [0.5, 1). Когда крутизна увеличивается, ответ фильтра приближается к идеальному полосовому ответу, но получившаяся длина фильтра и вычислительная стоимость операции фильтрации также увеличиваются. Смотрите Крутизну Полосового фильтра для получения дополнительной информации.

Отфильтруйте затухание полосы задерживания, заданное как пара, разделенная запятой, состоящая из 'StopbandAttenuation' и положительной скалярной величины в дБ.

Выходные аргументы

свернуть все

Фильтрованный сигнал, возвращенный как вектор, матрица или расписание с теми же размерностями как вход.

Полосовой фильтр используется в операции фильтрации, возвращенной как объект digitalFilter.

  • Используйте filter (d,x), чтобы отфильтровать x сигнала с помощью d.

  • Используйте fvtool (d), чтобы визуализировать ответ фильтра.

  • Используйте designfilt, чтобы отредактировать или сгенерировать цифровой фильтр на основе спецификаций частотной характеристики.

Больше о

свернуть все

Крутизна полосового фильтра

Аргумент 'Steepness' управляет шириной областей перехода фильтра. Чем ниже крутизна, тем шире область перехода. Чем выше крутизна, тем более узкий область перехода.

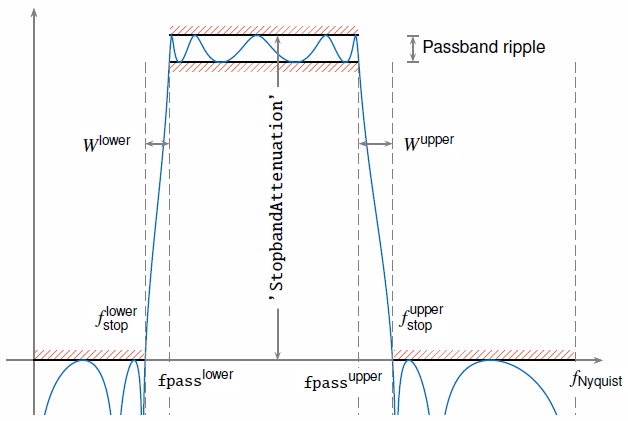
Чтобы интерпретировать крутизну фильтра, рассмотрите следующие определения:

  • Частота Найквиста, f Найквист, является самой высокой частотной составляющей сигнала, который может быть выбран на данном уровне без искажения. Найквисту f 1 год (×π рад/выборка), когда у входного сигнала нет времени информация и fs/2 герц, когда входной сигнал является расписанием или когда вы задаете частоту дискретизации.

  • Более низкие и верхние частоты полосы задерживания фильтра, f stoplower и f stopupper, являются частотами, ниже которых и выше который затухание равно или больше, чем значение, заданное с помощью 'StopbandAttenuation'.

  • Более низкой шириной перехода фильтра, W ниже, является fpass ниже – f stoplower, где fpass ниже является первым элементом fpass.

  • Верхней шириной перехода фильтра, верхний W, является f stopupper – верхний fpass, где верхний fpass является вторым элементом fpass.

  • Большинство неидеальных фильтров также ослабляет входной сигнал через полосу пропускания. Максимальное значение этого зависимого частотой затухания называется пульсацией полосы пропускания. Каждый фильтр, используемый bandpass, имеет пульсацию полосы пропускания 0,1 дБ.

Чтобы управлять шириной полос перехода, можно задать 'Steepness' как любой двухэлементный вектор, [s ниже, s, верхний], или скаляр. Когда вы задаете 'Steepness' как вектор, функцию:

  • Вычисляет более низкую ширину перехода как

    W ниже = (1 – s ниже) × fpass ниже.

    • Когда первый элемент 'Steepness' равен 0,5, ширина перехода составляет 50% fpass ниже.

    • Когда первый элемент 'Steepness' приближается 1, ширина перехода прогрессивно становится более узкой, пока это не достигает минимального значения 1% fpass ниже.

  • Вычисляет верхнюю ширину перехода как

    W, верхний = (1 – верхний s) × (f Найквист – верхний fpass).

    • Когда второй элемент 'Steepness' равен 0,5, ширина перехода составляет 50% (f Найквист – верхний fpass).

    • Когда второй элемент 'Steepness' приближается 1, ширина перехода прогрессивно становится более узкой, пока это не достигает минимального значения 1% (f Найквист – верхний fpass).

Когда вы задаете 'Steepness' как скаляр, функция разрабатывает фильтр с равными более низкими и верхними ширинами перехода. Значение по умолчанию 'Steepness' 0.85.

Смотрите также

Приложения

Функции

Введенный в R2018a

Документация Signal Processing Toolbox
Поддержка