Exponenta Banner

firpm

Паркует-McClellan оптимальный КИХ-проект фильтра

свернуть все на странице

Синтаксис

b = firpm(n,f,a)
b = firpm(n,f,a,w)
b = firpm(n,f,a,ftype)
b = firpm(n,f,a,lgrid)
[b,err] = firpm(___)
[b,err,res] = firpm(___)
b = firpm(n,f,fresp,w)
b = firpm(n,f,fresp,w,ftype)

Описание

пример

b = firpm(n,f,a) возвращает вектор - строку b, содержащий коэффициенты n+1 КИХ-фильтра порядка-n. Частота и амплитудные характеристики получившегося фильтра совпадают с данными векторами f и a.

пример

b = firpm(n,f,a,w) использование w, чтобы взвесить интервалы частоты.

b = firpm(n,f,a,ftype) использует тип фильтра, заданный 'ftype'.

b = firpm(n,f,a,lgrid) использует целочисленный lgrid, чтобы управлять плотностью сетки частоты.

[b,err] = firpm(___) возвращает максимальную высоту пульсации в err. Можно использовать это с любым из предыдущих входных синтаксисов.

[b,err,res] = firpm(___) возвращает характеристики частотной характеристики как структуру res.

b = firpm(n,f,fresp,w) возвращает КИХ-фильтр, амплитудные частотой характеристики которого лучше всего аппроксимируют ответ, возвращенный указателем на функцию fresp.

b = firpm(n,f,fresp,w,ftype) разрабатывает антисимметричные (нечетные) фильтры, где ftype задает фильтр как дифференциатор или Гильбертов преобразователь. Если вы не задаете ftype, вызов выполняется к fresp, чтобы определить свойство симметрии по умолчанию.

Примеры

свернуть все

Скрипт Open Live Script

Используйте алгоритм Парков-McClellan, чтобы разработать КИХ-полосовой фильтр порядка 17. Задайте нормированные частоты полосы задерживания 0.3π и 0.7π рад/выборка и нормированные частоты полосы пропускания 0.4π и 0.6π рад/выборка. Постройте идеальные и фактические ответы значения.

f = [0 0.3 0.4 0.6 0.7 1];
a = [0 0 1 1 0 0];
b = firpm(17,f,a);

[h,w] = freqz(b,1,512);
plot(f,a,w/pi,abs(h))
legend('Ideal','firpm Design')
xlabel 'Radian Frequency (\omega/\pi)', ylabel 'Magnitude'

Скрипт Open Live Script

Разработайте фильтр lowpass с частотой среза полосы пропускания на 1 500 Гц и частотой среза полосы задерживания на 2 000 Гц. Задайте частоту дискретизации 8 000 Гц. Потребуйте максимальной амплитуды полосы задерживания 0,01 и максимальной ошибки полосы пропускания (пульсация) 0,001. Получите необходимый порядок фильтра, нормированные ребра диапазона частот, амплитуды диапазона частот и веса с помощью firpmord.

[n,fo,ao,w] = firpmord([1500 2000],[1 0],[0.001 0.01],8000);
b = firpm(n,fo,ao,w);
fvtool(b,1)

Скрипт Open Live Script

Используйте алгоритм Парков-McClellan, чтобы создать 50-й порядок equiripple КИХ-полосовой фильтр, который будет использоваться с сигналами, выбранными на уровне 1 кГц.

N = 50;
Fs = 1e3;

Укажите, что полоса пропускания охватывает частоты между 200 Гц и 300 Гц и что область перехода по обе стороны от полосы пропускания имеет ширину 50 Гц.

Fstop1 = 150;
Fpass1 = 200;
Fpass2 = 300;
Fstop2 = 350;

Разработайте фильтр так, чтобы подгонка оптимизации взвесила низкочастотную полосу задерживания с весом 3, полоса пропускания с весом 1, и высокочастотную полосу задерживания с весом 100. Отобразите ответ значения фильтра.

Wstop1 = 3;
Wpass = 1;
Wstop2 = 100;

b = firpm(N,[0 Fstop1 Fpass1 Fpass2 Fstop2 Fs/2]/(Fs/2), ...
    [0 0 1 1 0 0],[Wstop1 Wpass Wstop2]);

fvtool(b,1)

Скрипт Open Live Script

Разработайте фильтр lowpass с частотой среза полосы пропускания на 1 500 Гц и частотой среза полосы задерживания на 2 000 Гц. Задайте частоту дискретизации 8 000 Гц. Потребуйте максимальной амплитуды полосы задерживания 0,01 и максимальной ошибки полосы пропускания (пульсация) 0,001. Получите необходимый порядок фильтра, нормированные ребра диапазона частот, амплитуды диапазона частот и веса с помощью firpmord.

[n,fo,ao,w] = firpmord([1500 2000],[1 0],[0.001 0.01],8000);
b = firpm(n,fo,ao,w);
fvtool(b,1)

Входные параметры

свернуть все

Отфильтруйте порядок, заданный как действительная положительная скалярная величина.

Нормированные точки частоты, заданные как вектор с действительным знаком. Аргумент должен быть в области значений [0, 1], где 1 соответствует частоте Найквиста. Число элементов в векторе всегда является кратным 2. Частоты должны быть в увеличивающемся порядке.

Желаемые амплитуды в точках, заданных в f, заданном как вектор. f и a должны быть той же длиной. Длина должна быть четным числом.

  • Желаемая амплитуда на частотах между парами точек (f (k), f (k +1)) для нечетного k является линейным сегментом, соединяющим точки (f (k), a (k)) и (f (k +1), a (k +1)).

  • Желаемая амплитуда на частотах между парами точек (f (k), f (k +1)) для k даже не задана. Областями между такими точками являются области перехода или области, которые не важны для конкретного приложения.

Веса раньше настраивали подгонку в каждом диапазоне частот, заданном как вектор с действительным знаком. Длина w является половиной длины f и a, таким образом, существует точно один вес на полосу.

Отфильтруйте тип, заданный или как 'hilbert' или как 'differentiator':

  • 'hilbert' — Поскольку линейная фаза фильтрует с нечетной симметрией (тип III и IV типа)

    Выходные коэффициенты в b повинуются отношению b (k) = –b (n + 2 – k), k = 1 ..., n + 1. Этот класс фильтров включает Гильбертов преобразователь, который имеет желаемую амплитуду 1 через целую полосу.

    Например, 

    h = firpm(30,[0.1 0.9],[1 1],'hilbert');

    разрабатывает аппроксимированного КИХ преобразователь Гильберта длины 31.

  • 'differentiator' — Для типа III и фильтров IV типа, с помощью специального метода взвешивания

    Для ненулевых амплитудных полос фильтр взвешивает ошибку фактором 1/f так, чтобы ошибка в низких частотах была намного меньше, чем в высоких частотах. Для КИХ-дифференциаторов, которые имеют амплитудную характеристику, пропорциональную частоте, эти фильтры минимизируют максимальную относительную погрешность (максимум отношения ошибки к желаемой амплитуде).

Управляйте плотностью сетки частоты, которая имеет примерно точки частоты (lgrid*n)/(2*bw), где bw является частью общего интервала диапазона частот [0,1] покрытый f. Увеличение lgrid часто приводит к фильтрам, которые более точно совпадают с фильтром equiripple, но которые занимают больше времени, чтобы вычислить. Значение по умолчанию 16 является минимальным значением, которое должно быть задано для lgrid.

Частотная характеристика, заданная как указатель на функцию. Функция вызвана из firpm с этим синтаксисом:

[dh,dw] = fresp(n,f,gf,w)

Аргументы подобны тем для firpm:

  • n является порядком фильтра.

  • f является вектором нормированных ребер диапазона частот, которые появляются монотонно между 0 и 1, где 1 частота Найквиста.

  • gf является вектором узлов решетки, которые были линейно интерполированы по каждому заданному диапазону частот firpm. gf определяет сетку частоты, в которой функция отклика должна быть оценена и содержит те же данные, возвращенные cfirpm в поле fgrid структуры opt.

  • w является вектором действительных, положительных весов, один на полосу, используемую во время оптимизации. w является дополнительным в вызове firpm; если не заданный, это установлено в единицу, взвешивающую прежде чем быть переданным fresp.

  • dh и dw являются желаемой комплексной частотной характеристикой и векторами веса полосы, соответственно, оцененный на каждой частоте в сетке gf.

Выходные аргументы

свернуть все

Отфильтруйте коэффициенты, возвращенные как вектор - строка из длины n + 1. Коэффициенты находятся в увеличивающемся порядке.

Максимальная высота пульсации, возвращенная как скаляр.

Характеристики частотной характеристики, возвращенные как структура. Структура res имеет следующие поля:

res.fgrid

Вектор сетки частоты, используемый для фильтра, разрабатывает оптимизацию

res.des

Желаемая частотная характеристика для каждой точки в res.fgrid

res.wt

Взвешивание для каждой точки в opt.fgrid

res.H

Фактическая частотная характеристика для каждой точки в res.fgrid

res.error

Ошибка в каждой точке в res.fgrid (res.des-res.H)

res.iextr

Вектор индексов в res.fgrid для экстремальных частот

res.fextr

Вектор экстремальных частот

Советы

Если вашему проекту фильтра не удается сходиться, проект фильтра не может быть правильным. Проверьте проект путем проверки частотной характеристики.

Если вашему проекту фильтра не удается сходиться, и получившийся проект фильтра не правилен, делайте попытку одного или нескольких из следующего:

  • Увеличьте порядок фильтра.

  • Ослабьте проект фильтра путем сокращения затухания в полосах задерживания и/или расширения областей перехода.

Алгоритмы

firpm разрабатывает КИХ-фильтр линейной фазы с помощью алгоритма Парков-McClellan [1]. Алгоритм Парков-McClellan использует алгоритм обмена Remez и Чебышевскую теорию приближения разработать фильтры с оптимальной подгонкой между желаемыми и фактическими частотными характеристиками. Фильтры оптимальны в том смысле, что максимальная погрешность между желаемой частотной характеристикой и фактической частотной характеристикой минимизирована. Фильтры разработали этот путь выставка equiripple поведение в их частотных характеристиках и иногда называются фильтрами equiripple. firpm показывает разрывы в голове и хвосте его импульсного ответа из-за этой equiripple природы.

Отношение между f и векторами a в определении желаемой частотной характеристики показывают на рисунке ниже.

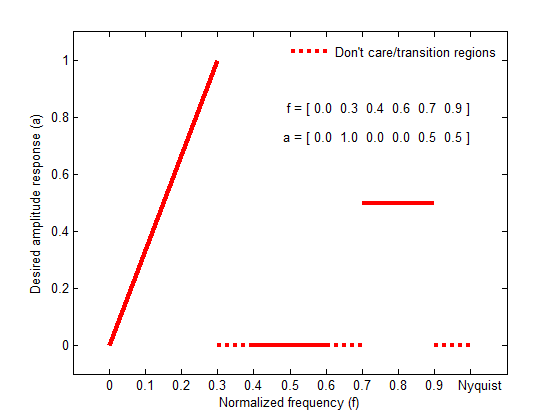
firpm всегда использует даже порядок фильтра для настроек с даже симметрией и ненулевой полосой пропускания на частоте Найквиста. Причина даже порядок фильтра состоит в том, что для импульсных ответов, показывающих даже симметрию и нечетные порядки, частотная характеристика на частоте Найквиста обязательно 0. Если вы задаете n с нечетным знаком, firpm постепенно увеличивает его 1.

firpm разрабатывает тип I, II, III и фильтры линейной фазы IV. Тип I и тип II являются значениями по умолчанию для n даже и нечетного n, соответственно, в то время как тип III (n даже) и вводит IV ( нечетный n) заданы с 'hilbert' или 'differentiator', соответственно, с помощью аргумента ftype.. Различные типы фильтров имеют различные симметрии и определенные ограничения на их частотные характеристики. (См. [5] для получения дополнительной информации.)

Линейный тип фильтра фазыОтфильтруйте порядокСимметрия коэффициентовОтвет H(f), f  = 0Response H(f), f  = 1 (Найквист)

Тип I

Даже

даже:

b(k)=b(n+2−k), k=1,...,n+1

Никакое ограничение

Никакое ограничение

Тип II

Нечетный

даже:

b(k)=b(n+2−k), k=1,...,n+1

Никакое ограничение

H (1)  = 0

firpm постепенно увеличивает порядок фильтра 1, при попытке создать фильтр типа II с ненулевой полосой пропускания на частоте Найквиста.

Тип III

Даже

нечетный:

b(k)=−b(n+2−k), k=1,...,n+1

H (0)  = 0

H (1)  = 0

Введите IVНечетный

нечетный:

b(k)=−b(n+2−k), k=1,...,n+1

H (0)  = 0

Никакое ограничение

Можно также использовать firpm, чтобы записать функцию, которая задает желаемую частотную характеристику. Предопределенным указателем на функцию частотной характеристики для firpm является @firpmfrf, который разрабатывает КИХ-фильтр линейной фазы.

Примечание

b = firpm(n,f,a,w) эквивалентен b = firpm(n,f,{@firpmfrf,a},w), где, @firpmfrf является предопределенным указателем на функцию частотной характеристики для firpm. При желании можно записать собственную функцию отклика. Используйте help private/firpmfrf и см. Создание указателя на функцию (MATLAB) для получения дополнительной информации.

Ссылки

[1] Комитет по Цифровой обработке сигналов Акустики IEEE, Речи, и Общества Обработки сигналов, программ редакторов для Цифровой обработки сигналов. Нью-Йорк: Нажатие IEEE, 1979, алгоритм 5.1.

[2] Комитет по Цифровой обработке сигналов Акустики IEEE, Речи и Общества Обработки сигналов, редакторы Выбрали Papers in Digital Signal Processing. Издание II. Нью-Йорк: Нажатие IEEE, 1976.

[3] Парки, Томас В. и К. Сидни Беррус. Создание цифровых фильтров. Нью-Йорк: John Wiley & Sons, 1987, p. 83.

[4] Rabiner, Лоуренс Р., Джеймс Х. Макклеллан и Томас В. Парки. “КИХ-Методы Создания цифровых фильтров Используя Взвешенное Чебышевское Приближение”. Продолжения IEEE®. Издание 63, Номер 4, 1975, стр 595–610.

[5] Оппенхейм, Алан V, Рональд В. Шафер и Джон Р. Бак. Обработка сигналов дискретного времени. Верхний Сэддл-Ривер, NJ: Prentice Hall, 1999, p. 486.

Расширенные возможности

Смотрите также

| | | | | | | | | | | |

Представлено до R2006a

Документация Signal Processing Toolbox
Поддержка