discontРазрывы функции
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
discont(f,x) discont(f,x, <Undefined>) discont(f,x, <Real>) discont(f,x = a .. b) discont(f,x = a .. b, <Undefined>) discont(f,x = a .. b, <Real>)
discont(f, x) вычисляет набор всех разрывов функционального f (x).
discont(f, x = a..b) вычисляет набор всех разрывов f (x), лежащий в интервале [a, b].
discont(f, x) возвращает набор чисел, содержащих все разрывы f, когда f рассматривается как функция x на съемочной площадке всех комплексных чисел, которые могут быть достигнуты x как значения, как задано предположениями на x. Обратите внимание на то, что вещественное число, которое является разрывом комплексной функции, не должно быть разрывом ограничения этой функции к набору вещественных чисел: рассмотрите, например, функцию, которая имеет ее разрез на вещественной оси, как в Примере 2 ниже.
Разрывы включают точки, где функция не задана, а также указывает, где функция задана, но не непрерывная. Если опция, Undefined используется, только точки, где функция не задана, возвращена.
Если опция, Real используется, он принят, что f и все его подвыражения представляют вещественные числа.
Если область значений, которую дан a..b, он принят, что x может взять значения только в интервале [a, b].
Набор, возвращенный discont, может содержать числа, которые не являются разрывами f. Смотрите Пример 7.
Если discont не может вычислить разрывы, то на символьный звонок discont отвечают; смотрите Пример 8.
discont может быть расширен к пользовательским математическим функциям через перегрузку. С этой целью встройте математическую функцию в функциональную среду и присвойте набор действительных разрывов к его слоту "realDiscont", набор его комплексных разрывов к его слоту "complexDiscont" и набор точек, где функция не задана к его слоту "undefined". Смотрите solve для обзора различных типов наборов. См. также Пример 8 ниже.
discont реагирует на свойства свободных параметров и в f, а также в a и в b. discont иногда реагирует на свойства x.
Функция gamma имеет полюса во всех целых числах меньше или равный нулю. Следовательно x -> gamma(x/2) имеет полюса во всех ровных целых числах меньше или равный нулю:
discont(gamma(x/2), x)
![]()
Логарифм имеет разрез на отрицательной вещественной оси; следовательно, это не непрерывно там. Однако его ограничение на вещественные числа непрерывно в каждой точке кроме нуля:
discont(ln(x), x), discont(ln(x), x, Real)
![]()
Функциональный sign задан везде; это не непрерывно в нуле:
discont(sign(x), x), discont(sign(x), x, Undefined)
![]()
Если область значений дана, только разрывы в той области значений возвращены.
discont(1/x/(x - 1), x = 0..1/2)
![]()
Область значений может иметь произвольные арифметические выражения как контуры. discont неявно принимает, что правильный контур больше или равен левому контуру:
discont(1/x, x = a..b)
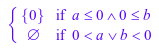
Как видно из предыдущего примера discont реагирует на свойства свободных параметров (потому что piecewise делает). Результат также зависит от свойств x: это может не использовать значения, которые x не может взять так или иначе из-за его свойств.
assume(x > 0): discont(1/x, x)
![]()
delete x:
Иногда, discont возвращает соответствующее надмножество набора разрывов:
discont(piecewise([x<>0, x*sin(1/x)], [x=0, 0]), x)
![]()
Если discont не может определить разрывы заданной функции, то discont принимает, что функция непрерывна и возвращает пустое множество:
delete f: discont(f(x), x)
![]()
Можно предоставить необходимую информацию путем добавления слотов в f. Например, примите, что f еще не непрерывен в 1, но везде; и это также его ограничение на вещественные числа остается прерывистым в 1. После добавления соответствующих слотов discont заботится, чтобы обработать f правильно также, если это появляется в более сложном выражении:
f:= funcenv(x->procname(x)):
f::realDiscont:= {1}:
f::complexDiscont:= {1}:
discont(f(sin(x)), x=-4..34)![]()
Мы задаем функцию, которая реализует логарифм, чтобы базироваться 2. Для простоты мы позволяем ему всегда возвратить неоцененный вызов функции. Логарифм имеет разрез на отрицательной вещественной оси; его ограничение на реалы непрерывно везде кроме в нуле:
binlog := funcenv(x -> procname(x)):
binlog::realDiscont := {0}:
binlog::undefined := {0}:
binlog::complexDiscont := Dom::Interval(-infinity, [0]):
discont(binlog(x), x);
discont(binlog(x), x=-2..2, Real);
discont(binlog(x), x=-2..2, Undefined)![]()
![]()
![]()
|
Арифметическое выражение, представляющее функцию в |
| |
|
Контуры интервала: арифметические выражения |
|
Возвратите только те точки, где |
|
Примите, что все подвыражения |
Установите — смотрите страницу справки для solve для обзора всех типов наборов — или символьный вызов discont.
f