gammaГамма функция
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
gamma(x) gamma(iv)
gamma(x) представляет гамма функцию![]() .
.
Гамма функция задана для всех сложных аргументов кроме особых точек 0, - 1, - 2, ….
Гамма функция связана с функцией факториала: gamma(x) = fact(x - 1) = (x - 1)! для всех положительных целых чисел x.
Если x является значением с плавающей точкой, то gamma возвращает значение с плавающей точкой. Если x является интервалом с плавающей точкой, gamma возвращает интервал с плавающей точкой. Если x является положительным целым числом, не больше, чем значение, данное Pref::autoExpansionLimit(), то целое число возвращено. (Используйте expand(gamma(x)), чтобы получить целочисленное значение для больших целых чисел x.), Если x является рациональным числом доменного типа DOM_RAT, не больше, чем значение, данное Pref::autoExpansionLimit(), то функциональное отношение Γ (x + 1) = x Γ (x) применяется, чтобы “нормировать” результат. (Снова, используйте expand(gamma(x)), чтобы осуществить эту нормализацию для больших рациональных чисел x.) Функциональное отношение
![]()
применяется, если![]() рациональное число доменного типа
рациональное число доменного типа DOM_RAT, который является целочисленным кратным![]() или
или![]() . Вызов
. Вызов gamma(1/2) приводит к sqrt(PI). Вызов gamma(infinity) приводит к infinity. Для всех других аргументов возвращен символьный вызов функции.
Атрибут с плавающей точкой gamma является функцией ядра, то есть, оценка с плавающей точкой быстра.
Атрибут expand переписывает gamma(x) при помощи функционального уравнения Γ (x + 1) = x Γ (x), отражательная формула
![]() ,
,
и формула умножения Гаусса для Γ (k x), когда k является положительным целым числом. Смотрите Пример 3. Для числового x функциональное уравнение используется, чтобы переключить аргумент к области значений 0 < x < 1.
Функциональные уравнения для gamma приводят к различным тождествам для lngamma, который может быть применен через expand. Смотрите Пример 3.
Логарифмическая производная gamma реализована дигамма-функцией psi.
Когда названо аргументом с плавающей точкой, функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Вызовите gamma с точными и символьными входными данными:
gamma(15), gamma(3/2), gamma(-3/2), gamma(sqrt(2)), gamma(x + 1)
![]()
Вызовите gamma с аргументами с плавающей точкой:
gamma(11.5), gamma(2.0 + 10.0*I)
![]()
gamma сингулярен для неположительных целых чисел:
gamma(0)
Error: Singularity. [gamma]
diff, expand, float, limit и series обрабатывают выражения, включающие gamma:
diff(gamma(x^2 + 1), x)
![]()
float(ln(3 + gamma(sqrt(PI))))
![]()
expand(gamma(x + 2))
![]()
expand(gamma(2*x))
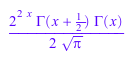
expand(gamma(2*x - 1))
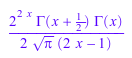
limit(1/gamma(x), x = infinity)
![]()
limit(gamma(x - 4)/gamma(x - 10), x = 0)
![]()
series(gamma(x), x = 0, 3)

Стерлингская формула получена как асимптотический ряд:
series(gamma(x), x = infinity, 4)
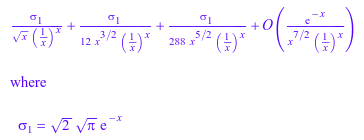
ln функции логарифма имеет разрез вдоль отрицательной действительной полу оси, где значения переходят на 2 π i при пересечении сокращения. В следующем графике мнимой части логарифма гаммы функционируют строки в комплексной плоскости z с![]() и
и![]() явно видимы как разрывы:
явно видимы как разрывы:
plotfunc3d(Im(ln(gamma(x + I*y))), x = -10 .. 10, y = -10 .. 10,
Submesh = [2, 2], CameraDirection = [0, -1, 1000]):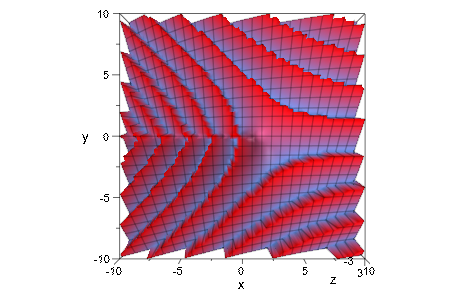
Функциональный lngamma(z), однако, добавляет подходящие целочисленные множители 2 π i к ln(gamma(z)), делающему функцию, аналитичную в комплексной плоскости с разрезом вдоль отрицательной действительной полу оси:
plotfunc3d(Im(lngamma(x + I*y)), x = -10 .. 10, y = -10 .. 10,
Submesh = [2, 2], CameraDirection = [0, -1, 1000]):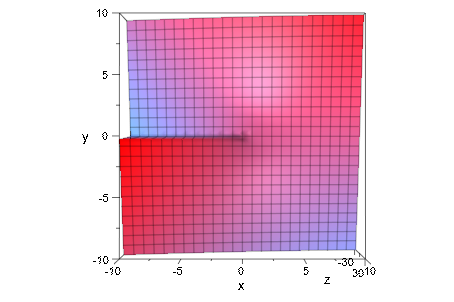
| |
|
Арифметическое выражение или интервал с плавающей точкой.
x