piecewiseОбласть условно заданных объектов
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
piecewise([cond1,value1], [cond2,value2], …, <[Otherwise,valueN]>, <ExclusiveConditions>)
piecewise([cond1, value1], [cond2, value2], ...) задает условный объект, который равняется value1, если cond1 доказуемо верен, value2, если cond2 доказуемо верен и так далее. Как правило, такие объекты задают кусочные функции или выражают решения на основе анализа случая свободных параметров математической проблемы. Смотрите Пример 1.
Парный [condition, value] называется ответвлением. Если condition является доказуемо ложным, то piecewise отбрасывает целое ответвление. Если condition доказуемо верен, то piecewise возвращает соответствующий value. Если никакое условие в кусочном объекте не доказуемо верно, piecewise возвращает объект типа piecewise, который содержит все ответвления, за исключением ответвлений с доказуемо ложными условиями.
Если все условия являются доказуемо ложными, или если вы вызываете piecewise без каких-либо ответвлений, то piecewise возвращает undefined. Смотрите Пример 1.
Условия не должны быть исчерпывающими или исключительными. Если условия содержат параметры, и вы заменяете значениями параметры, все условия могут стать ложными. Кроме того, несколько условий могут стать верными.
Если несколько условий одновременно верны, piecewise возвращает значение от первого ответвления, которое содержит условие, распознанное верным. Гарантируйте, что все значения, соответствующие истинным условиям, имеют то же математическое значение. Не полагайтесь на систему, чтобы распознать первое математически истинное условие верным. Также можно использовать опцию ExclusiveConditions, чтобы зафиксировать порядок ответвлений.
piecewise([cond1, value1], [cond2, value2], ..., [Otherwise, valueN]) проверяет условия, и, если они не удовлетворены, отбрасывания их, и возвращает valueN. Условие Otherwise происходит в последнем ответвлении. Это может произойти только однажды. Это остается неизменным пока существуют другие ответвления, но это обработано как верное, когда все другие ответвления отбрасываются, потому что их условия ложные. Смотрите Пример 2.
Система проверяет истину условий для текущих значений и свойств всех включенных идентификаторов каждый раз, когда это оценивает объект типа piecewise. Таким образом это упрощает кусочные выражения под всевозможными предположениями.
Объекты piecewise могут быть вложены: и условия и значения могут быть самими объектами piecewise. piecewise автоматически “сглаживает” такие объекты. Например, piecewise([conditionA, piecewise([conditionB, valueC])]) становится piecewise([conditionA and conditionB, valueC]). Смотрите Пример 3.
Арифметические и относящиеся к теории множеств операции работают на объекты piecewise, если эти операции заданы для всех значений, содержавшихся в ответвлениях. Если f является такой операцией, и p1, p2, ... объекты piecewise, то f(p1, p2, ...) является объектом piecewise, состоящим из всех ответвлений формы [cond1 and cond2 and ..., f(value1, value2, ...)], где [cond1, value1] является ответвлением p1, [cond2, value2] является ответвлением p2 и так далее. Другими словами, применение f коммутируется с любым присвоением на свободные параметры в условиях. Смотрите Пример 4.
Объекты piecewise могут также быть смешаны с другими объектами в таких операциях. В таких случаях, если p1 не является объектом piecewise, система обрабатывает его как объект piecewise с единственным ответвлением [TRUE, p1]. Смотрите Пример 5.
diff, float, limit, int и подобные функции обрабатывают выражения, включающие piecewise. Когда вы используете аргумент piecewise в унарных операторах и функциях с одним аргументом, система сопоставляет оператор или функцию к значениям в каждом ответвлении. Смотрите Пример 6, Пример 7 и Пример 8.
piecewise отличается от if и операторов ветвления case. Во-первых, piecewise использует механизм свойства при решении истины условий. Поэтому результат зависит от свойств идентификаторов, которые появляются в условиях. Во-вторых, piecewise обрабатывает условия математически, в то время как if и case оценивают их синтаксически. В-третьих, piecewise внутренне сортирует ответвления. Если условия в нескольких ответвлениях верны, piecewise может возвратить любое из этих ответвлений. Смотрите Пример 9.
Опция ExclusiveConditions фиксирует порядок ответвлений в кусочном выражении. Если условие в первом ответвлении возвращает TRUE, то piecewise возвращает значение от первого ответвления. Если истинное условие появляется в дальнейшем ответвлении, то piecewise возвращает значение от того ответвления и удаляет все последующие ответвления. Таким образом piecewise с ExclusiveConditions очень похож на оператор if-elif-end_if. Тем не менее, piecewise с ExclusiveConditions все еще учитывает предположения на идентификаторах и обрабатывает условия математически, в то время как if-elif-end_if обрабатывает их синтаксически. Смотрите Пример 10.
piecewise учитывает свойства идентификаторов.
Задайте этот прямоугольный функциональный f. Без дополнительной информации о переменной x система не может оценить условия к TRUE или FALSE. Поэтому это возвращает объект piecewise.
f := x -> piecewise([x < 0 or x > 1, 0], [x >= 0 and x <= 1, 1])

Вызовите функциональный f со следующими аргументами. Каждый раз, когда вы вызываете эту кусочную функцию, система проверяет условия в свои ответвления и выполняет функцию.
f(0), f(2), f(I)
![]()
Создайте эту кусочную функцию с помощью синтаксиса, который включает Otherwise:
pw:= piecewise([x > 0 and x < 1, 1], [Otherwise, 0])

Оцените pw для этих трех значений:
pw | x = 1/2; pw | x = 2; pw | x = I;
![]()
![]()
![]()
Для дальнейших вычислений удалите идентификатор pw:
delete pw:
Создайте это вложенное кусочное выражение. MuPAD® сглаживается, вложил объекты piecewise.
p1 := piecewise([a > 0, a^2], [a <= 0, -a^2]): piecewise([b > 0, a + b], [b = 0, p1 + b], [b < 0, a + b])
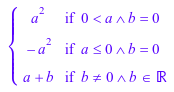
Найдите сумму этих кусочных функций. Можно выполнить большинство операций на кусочных функциях тот же путь, как вы были бы по обычным арифметическим выражениям. Результат арифметической операции только задан в точках, где все аргументы заданы:
piecewise([x > 0, 1], [x < -3, x^2]) + piecewise([x < 2, x])

Решите это уравнение. Решатель возвращает результат как кусочный набор:
S := solve(a*x = 0, x)

Можно использовать относящиеся к теории множеств операции, работают на такие наборы. Например, найдите пересечение этого набора и интервала (3, 5):
S intersect Dom::Interval(3, 5)
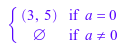
Много унарных функций перегружаются для piecewise путем отображения их с объектами во всех ответвлениях входа:
f := piecewise([x >= 0, arcsin(x)], [x < 0, arccos(x)]): sin(f)

Найдите предел этой кусочной функции:
limit(piecewise([a > 0, x],[a < 0 and x > 1, 1/x],
[a < 0 and x <= 1, -x]), x = infinity)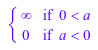
Найдите интеграл этой кусочной функции:
int(piecewise([x < 0, x^2], [x > 0, x^3]), x = -1..1)
![]()
Создайте эту кусочную функцию. Здесь, piecewise не может определить, является ли какое-либо ответвление TRUE или FALSE. Чтобы сделать это, piecewise нужна дополнительная информация об идентификаторе a.
p1 := piecewise([a = 0, 0], [a <> 0, 1/a])
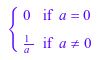
Создайте подобную структуру при помощи if-then-else. Структура if-then-else оценивает условия синтаксически. Здесь, a = 0 является технически ложным, потому что идентификатор a и целочисленный 0 является различными объектами.
p2 := (if a = 0 then 0 else 1/a end)
![]()
piecewise принимает свойства во внимание идентификаторов:
p1 := piecewise([a + b = 0, 0], [Otherwise, 1/a]) assuming a + b = 0
![]()
if-then-else не делает:
p2 := (if a + b = 0 then 0 else 1/a end) assuming a + b = 0
![]()
Для дальнейших вычислений удалите идентификаторы a, b, p1 и p2:
delete a, b, p1, p2:
Создайте это кусочное выражение:
p := piecewise([x > 0, 1], [y > 0, 2])
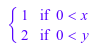
Выполните выражение в y = 1:
p | y = 1
![]()
Теперь, создайте кусочное выражение с теми же ответвлениями, но на этот раз используйте ExclusiveConditions, чтобы зафиксировать порядок ответвлений. Когда вы используете эту опцию, любое ответвление может быть верным, только если предыдущие ответвления являются ложными.
pE := piecewise([x > 0, x], [y > 0, y], ExclusiveConditions)

Выполните выражение в y = 1:
pE | y = 1

Когда вы используете ExclusiveConditions, piecewise действует одинаково как оператор if-then-else, но не игнорирует свойства идентификаторов. Например, установите предположение что x = 0:
assume(x = 0)
Вызов функции piecewise возвращается 0, потому что он использует предположение на идентификаторе x:
p := piecewise([x = 0, x], [Otherwise, 1/x^2])
![]()
Соответствующий оператор if-then-else игнорирует предположение, и, поэтому, возвращает 1/x^2:
pIf := (if x = 0 then x else 1/x^2 end)
![]()
Для дальнейших вычислений удалите идентификаторы p, pE, x и pIf:
delete p, pE, x, pIf:
Найдите набор предельных точек этой кусочной функции путем вызова limit с опцией Intervals:
limit(piecewise([a > 0, sin(x)], [a < 0 and x > 1, 1/x],
[a < 0 and x <= 1, -x]), x = infinity, Intervals)
Перепишите функцию sign с точки зрения объекта piecewise:
f := rewrite(sign(x), piecewise)

Создайте этот объект piecewise:
f := piecewise([x > 0, 1], [x < -3, x^2])

Извлеките конкретное условие или объект:
piecewise::condition(f, 1), piecewise::expression(f, 2)
![]()
Индексный оператор имеет то же значение как piecewise::expression и может быть введен быстрее:
f[2]
![]()
Функция piecewise::branch извлекает целые ответвления:
piecewise::branch(f, 1)
![]()
Можно сформировать другой объект piecewise из ответвлений, для которых условие удовлетворяет данный критерий выбора или разделило вход в два объекта piecewise как системные функции, select и split делают это для списков:
piecewise::selectConditions(f, has, 0)
![]()
piecewise::splitConditions(f, has, 0)
![]()
Можно также создать копию f с некоторыми ответвлениями, добавленными или удаленными:
piecewise::remove(f, 1)
![]()
piecewise::insert(f, [x > -3 and x < 0, sin(x)])
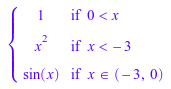
|
Булевы константы или выражения, представляющие логические формулы |
|
Произвольные объекты |
|
Идентификатор, который задает последнее условие. Это условие всегда обрабатывается как истинное условие. |
|
Опция |
Операнды объекта piecewise (ответвления) являются парами, состоящими из условия и значения, допустимого при том условии.
Методы, перегружающие системные функции всегда, принимают, что были названы через перегрузку, и что существует некоторый условно заданный объект среди их аргументов. Все другие методы не принимают, что один из их аргументов имеет тип piecewise. Это упрощает использование piecewise: всегда позволяется ввести p:=piecewise(...) и вызвать некоторый метод piecewise с p в качестве аргумента. Вы не должны заботиться об особом случае, где p не имеет типа piecewise, потому что некоторое условие в его определении верно, или все условия являются ложными.