`limit`

Вычислите предел

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

limit(f, x, <Left | Right | Real>, <Intervals>, <NoWarning>)
limit(f, x = x₀, <Left | Right | Real>, <Intervals>, <NoWarning>)

Описание

_{limit(f, x = x0, Real)} вычисляет двунаправленный предел.

_{limit(f, x = x0, Left | Right)} вычисляет односторонний предел, соответственно.

_{limit(f, x = x0, Intervals)} вычисляет набор, содержащий все предельные точки.

limit(f, x = x0, <Real>) вычисляет двунаправленный предел f, когда x склоняется к x0 на вещественной оси. Предельная точка x0 может быть не использован, в этом случае limit, принимает x0 = 0.

Если предельная точка, x0 является infinity или - ∞, то предел взят слева к infinity или справа к - ∞, соответственно.

Если доказуемо никакой предел не существует, то undefined возвращен. Смотрите Пример 2.

limit(f, x = x0, Left) возвращает предел, когда x склоняется к x0 слева. limit(f, x = x0, Right) возвращает предел, когда x склоняется к x0 справа. Смотрите Пример 2.

Если нельзя определить, существует ли предел или не может определить свое значение, то символьное limit возвращено. Смотрите Пример 3. То же самое содержит, в случае, если опция, которую дан Intervals, если никакая информация на съемочной площадке предельных точек не могла бы быть получена.

Если f содержит параметры, то limit реагирует на свойства тех параметров, установленных assume. Смотрите Пример 5. Это может также возвратить анализ случая (piecewise) в зависимости от этих параметров.

Можно вычислить предел кусочной функции. Условия, которые вы используете, чтобы задать кусочную функцию, могут зависеть от предельной переменной. Смотрите Пример 6.

Внутренне, limit пытается определить предел от последовательного расширения f вокруг x = x0, вычисленного через series. Может быть необходимо увеличить значение переменной окружения ORDER в порядке найти предел.

Примечание

limit работает на символьном уровне и не должен быть вызван аргументами, содержащими аргументы с плавающей точкой.

Взаимодействия среды

Функция чувствительна к переменной окружения ORDER, который определяет количество по умолчанию условий в последовательных вычислениях (см. series).

Учтены свойства идентификаторов, установленных assume.

Примеры

Пример 1

Следующая команда вычисляет:

limit((1 - cos(x))/x^2, x)

Возможное определение e дано пределом последовательности для:

limit((1 + 1/n)^n, n = infinity)

Вот более комплексный пример:

limit(
  (exp(x*exp(-x)/(exp(-x) + exp(-2*x^2/(x+1)))) - exp(x))/x,
  x = infinity
)

Пример 2

Двунаправленный предел для не существует:

limit(1/x, x = 0)

Можно вычислить односторонние пределы слева и справа путем передачи опций Left и Right, соответственно:

limit(1/x, x = 0, Left), 
limit(1/x, x = 0, Right)

Пример 3

Если limit не может вычислить предел, то на символьный звонок limit отвечают:

delete f: limit(f(x), x = infinity)

Пример 4

Функциональный sin (x) колеблется для между - 1 и 1; никакие предельные точки вне того интервала не существуют:

limit(sin(x), x = infinity, Intervals)

На самом деле все элементы возвращенного интервала являются предельными точками. Это не должно иметь место в целом. В следующем примере нижний предел и выше предел на самом деле и, соответственно:

limit(sin(1/x) + cos(1/x), x = 0, Intervals)

Пример 5

limit не может вычислить предел x ⁿ для без дополнительной информации о параметре n:

assume(n in R_): 
limit(x^n, x = infinity)

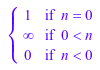
Мы сразу можем также assume, что n> 0 и не получает анализа случая затем:

assume(n > 0): limit(x^n, x = infinity)

Точно так же мы можем принять что n <0:

assume(n < 0): limit(x^n, x = infinity)

delete n:

Пример 6

Вычислите предел кусочной функции:

limit(piecewise([x^3 > 10000*x, 1/x],
                [x^3 <= 10000*x, 10]),
                            x = infinity)

Пример 7

Вычислите пределы неполной Гамма функции:

limit(igamma(z, t), t = infinity);
limit(igamma(z, t), t = 0)

Параметры

`f`	Арифметическое выражение, представляющее функцию в `x`
`x`	Идентификатор
`_x0`	Предельная точка: арифметическое выражение, возможно `infinity` или `-infinity`

Опции

`Left`, `Real`, `Right`	Это управляет направлением предельного вычисления. Опция `Real` является случаем по умолчанию и означает двунаправленный предел (т.е. нет никакой потребности задать эту опцию).
`Intervals`	Или `TRUE` или `FALSE`, `FALSE` по умолчанию. Если эта опция установлена в `TRUE`, то надмножество набора всех предельных точек возвращено. Если результат содержит только один элемент, тот элемент является пределом; с другой стороны, если это содержит больше элементов, не все они - обязательно предельные точки, такие, что предел может, тем не менее, существовать.
`NoWarning`	Если эта опция установлена в `TRUE`, никакие предупреждающие сообщения не распечатаны на экране. Значением по умолчанию является `FALSE`.

Возвращаемые значения

арифметическое выражение. Если опция, которую Intervals был дан, результат, (конечна или бесконечна) набор.

Перегруженный

f

Алгоритмы

limit использует алгоритм на основе тезиса Доминика Грунца: “При Вычислении Пределов в Символьной Системе Манипуляции”, Швейцарская высшая техническая школа, Цюрих, Швейцария, 1995. Если это перестало работать, это пытается продолжить рекурсивно; наконец, это делает попытку последовательного расширения.

Документация