solveРешите уравнения и неравенства
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Для функции solve в MATLAB® смотрите solve.
solve(eq,x,options) solve(eq,x = a .. b,options) solve(eq,vars,options) solve(eq,options) solve(eqs,x,options) solve(eqs,vars,options) solve(eqs,options) solve(ODE) solve(REC)
solve(eq, x) возвращает набор всех сложных решений уравнения или неравенства eq относительно x.
solve(eq, x = a..b) возвращает набор всех решений в закрытом интервале Dom::Interval([a, b]).
solve(eq, vars) решает уравнение для переменных vars.
solve(eqs, x) решает систему eqs для переменной x.
solve(eqs, vars) решает систему eqs уравнений для переменных vars.
Функция solve обеспечивает объединенный интерфейс ко множеству специализированных решателей. Смотрите Выбор Решателя.
Если вы не задаете indeterminates, для которого вы хотите решить уравнение, неравенство или систему, решатель использует набор всего indeterminates. Indeterminates должен быть идентификаторами или индексированными идентификаторами. Вы не можете использовать математические константы, такие как PI, ЭЙЛЕР, и так далее, как indeterminates. Решатель отбрасывает indeterminates, которые появляются только в именах функций или индексах. Смотрите Пример 12.
Если вы задаете список indeterminates, для которого вы хотите решить уравнение, неравенство или систему, решатель сортирует компоненты получившихся векторов решения согласно порядку indeterminates, который вы использовали. Если вы задаете indeterminates как набор, MuPAD® может изменить порядок indeterminates.
solve(eq, vars) эквивалентен solve([eq], vars).
Решатель может возвратить следующие типы наборов:
Конечные множества (вводят DOM_SET).
Символьные вызовы solve.
Нулевые наборы полиномов (вводят RootOf). Решатель возвращает набор этого типа, если это не может решить уравнение явным образом с точки зрения радикалов. Решатель также может возвратить этот тип набора, когда вы используете опцию MaxDegree.
Относящиеся к теории множеств выражения, такие как "_union", "_intersect" и "_minus".
Символьные вызовы solvelib::Union. Эти вызовы представляют объединения по параметрическим системам наборов.
ℂ, ℝ, ℚ и ℤ (вводят solvelib::BasicSet), наборы.
Интервалы (вводят Dom::Interval).
Отобразите наборы функций (введите Dom::ImageSet).
Кусочные объекты, в которых каждое ответвление задает набор одного из допустимых типов (вводят piecewise).
MuPAD может использовать наборы этих типов, исключая интервалы и основные наборы, чтобы представлять наборы векторов (для решений систем). При решении системы MuPAD также может возвратить решение в форме S n (n - сворачивают декартову степень набора S скаляров). Здесь S является набором любого типа, возвращенного solve.
Для возвращенных наборов решения можно использовать относящиеся к теории множеств операции, такие как intersect, union и minus. Кроме того, можно использовать pointwise-заданные арифметические операции, такие как +, *, и так далее. Чтобы извлечь элементы набора, используйте функцию solvelib::getElement. Чтобы протестировать, конечен ли набор решения, возвращенный solve, используйте функциональный solvelib::isFinite. Смотрите Пример 2
Для систем решатель возвращает набор векторов или набор списков уравнений. Чтобы указать, что решатель должен возвратить набор векторов, используйте опцию VectorFormat. Смотрите Пример 10.
По умолчанию solve(eq, x) возвращает только решения, сопоставимые со свойствами x. Чтобы проигнорировать свойства x, используйте опцию IgnoreProperties. Эта опция полезна, когда вы решаете систему уравнений больше чем для одной переменной. Смотрите Пример 13.
a <= b неравенства или a < b содержат только, когда обе стороны представляют вещественные числа. В частности, a = b не подразумевает тот a <= b для комплексных чисел.
Можно записать пользовательские области для уравнений специальных типов, и затем перегрузки solve для этих областей. MuPAD использует эту функцию для уравнений повторения и дифференциала. Смотрите ode, ode::solve и страницы справки rec.
Функция solve является символьным решателем. Если вы хотите использовать числовые методы, смотрите страницу справки numeric::solve для доступных параметров и примеров.
Если вход содержит числа с плавающей запятой, решатель заменяет их аппроксимированными рациональными значениями. Точность этих приближенных значений зависит от переменной окружения DIGITS. Если solve находит решение, MuPAD внутренне вызывает функцию float для того решения, и затем возвращает результат. Если символьный решатель возвращает unevaluated, MuPAD вызывает numeric::solve. Смотрите Пример 16.
Если числитель содержит учтенный полином с кратностью, больше, чем 1, решатель не проверяет, что несколько поддерживают нули в знаменателе. Смотрите Пример 17.
solve реагирует на свойства идентификаторов.
Решите следующее уравнение. Как правило, для уравнений с конечным числом решений, решатель возвращает набор типа DOM_SET:
S := solve(x^4 - 5*x^2 + 6*x = 2, x)
![]()
Присвойте отдельные решения переменных путем индексации в S:
sol1 := S[1]
![]()
Решатель может также возвратить бесконечный дискретный набор решений:
S := solve(sin(x*PI/7) = 0, x)
![]()
Чтобы выбрать решения в конкретном конечном интервале, найдите пересечение набора решения с интервалом:
S intersect Dom::Interval(-22, 22)
![]()
Также задайте интервал при вызове решателя. Например, вычислите решения в интервале [-22, 22]:
solve(sin(x*PI/7) = 0, x = -22..22)
![]()
delete S:
Используйте функцию solve, чтобы решить неравенства. Как правило, набор решения неравенства является интервалом или объединением интервалов:
solve(x^2 > 5, x)
![]()
Решите следующее неравенство. Решение включает набор всех комплексных чисел, исключая![]() и
и![]() :
:
solve(x^2 <> 7, x)
![]()
Решатель может возвратить решение как объединение бесконечного семейства наборов. Функция solvelib::Union представляет такие бесконечные объединения в MuPAD:
solve(sin(x)*cos(x) > 1/4, x, Real)
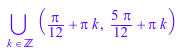
Если уравнение содержит символьные параметры, решатель возвращает кусочное решение. Например, решите квадратное уравнение ax 2 + bx + c = 0:
S := solve(a*x^2 + b*x + c, x)
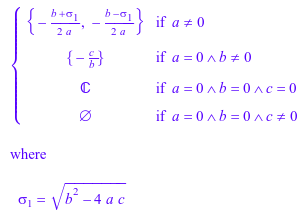
Теперь, оцените решение, принимающее, что a не равен 0:
assume(a <> 0): S
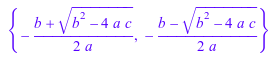
delete S: unassume(a):
По умолчанию решатель пытается найти все возможные решения. Следующее неравенство имеет и действительные и сложные решения. Например,![]() одно из решений. Решатель не может найти представление закрытой формы всех возможных решений:
одно из решений. Решатель не может найти представление закрытой формы всех возможных решений:
solve(x + 1/x > 0, x)
![]()
С опцией Real решатель вычисляет только действительные решения. Представление закрытой формы всех действительных решений того уравнения является интервалом всех вещественных чисел от 0 до бесконечности:
solve(x + 1/x > 0, x, Real)
![]()
Решите это уравнение. По умолчанию решатель возвращает полное, а скорее долго и сложное решение:
solve(x^(7/2) + 1/x^(7/2) = 1, x)
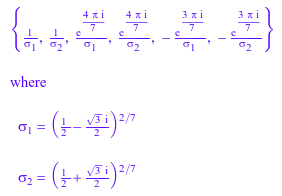
Используя IgnoreAnalyticConstraints, часто можно получать более простые результаты:
solve(x^(7/2) + 1/x^(7/2) = 1, x, IgnoreAnalyticConstraints)
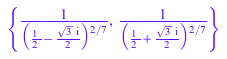
Используя эту опцию, также можно получить неправильные результаты:
solve(arcsin(x) = C, x, IgnoreAnalyticConstraints) assuming C > 10
![]()
Всегда проверяйте результаты, полученные с этой опцией:
testeq(arcsin(sin(C)), C)
![]()
Опция IgnoreAnalyticConstraints также может привести к неполным результатам:
solve(x^(5/2) = 1, x)
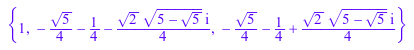
solve(x^(5/2) = 1, x, IgnoreAnalyticConstraints)
![]()
С опцией IgnoreAnalyticConstraints решатель может умножить обе стороны уравнения по любому выражению, кроме 0. В следующем примере решатель умножает обе стороны уравнения![]() . Решатель не считает особый случай
. Решатель не считает особый случай x = y = 0:
solve(1/sqrt(x) = 1/sqrt(y), IgnoreAnalyticConstraints)
![]()
Результат не допустим для x = y = 0.
Когда вы решаете систему уравнений, MuPAD пытается представлять решения как набор списков замен:
solve([x^2 + y = 1, x + y^2 = 1], [x, y])

Если вы используете опцию VectorFormat, MuPAD возвращает решение как набор векторов:
solve([x^2 + y = 1, x + y^2 = 1], [x, y], VectorFormat)
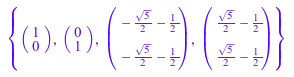
Правые стороны возвращенных замен могут содержать сгенерированные идентификаторы. В этом случае замена каждым из этих идентификаторов с комплексным числом дает решение системы. Можно получить все решения путем замены сгенерированными идентификаторами со всеми комплексными числами:
sys:= [x + y + z = 2, x + y^2 + z^2 = 4]: solve(sys, [x, y, z])

Если вы используете опцию VectorFormat, решатель возвращает решение как бесконечное множество векторов в обычном математическом обозначении:
solve(sys, [x, y, z], VectorFormat); delete sys:
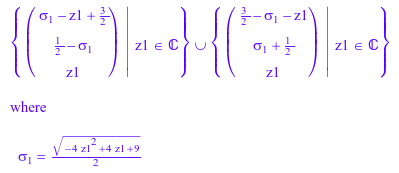
Можно задать переменную, для которой вы хотите решить уравнение как список одной записи. В этом случае решатель возвращает решение с помощью выходного формата, обычно используемого для систем:
solve(x = x, x), solve(x = x, [x])
![]()
Если вы не задаете indeterminates (переменные, для которых вы хотите решить уравнение), решатель использует набор всего indeterminates, который это может найти в том уравнении:
solve(x^2 = 3)
![]()
Решатель не расценивает операторы и индексы как indeterminates. Поэтому решатель не обрабатывает f и y как indeterminates в следующем уравнении:
solve(f(x[y]) = 7)
![]()
Если вы устанавливаете предположение на переменной, для которой вы хотите решить уравнение, решатель возвращает только результаты, совместимые с тем предположением. Например, примите, что x представляет действительное положительное число. Затем решите следующее уравнение:
assume(x, Type::Positive): solve(x^4 = 1, x)
![]()
Без того предположения решатель возвращает все сложные решения:
unassume(x): solve(x^4 = 1, x)
![]()
Чтобы получить кратность корней полинома, используйте опцию Multiple. Например, полиномиальный x 3 + 2 x2 + x имеет два корня. Кратность x = - 1 равняется 2. Кратность x = 0 равняется 1:
solve(x^3 + 2*x^2 + x, x, Multiple)
![]()
Предположим, вы хотите решить следующую систему уравнений для двух переменных, x и y. Предположим, вы хотите избежать обратных подстановок при решении этой системы. Чтобы отключить обратные подстановки, используйте опцию BackSubstitution = FALSE. Задайте список переменных так, чтобы x появился справа от y. Теперь, решение для переменной y может содержать переменную x:
solve({x^2 + y = 1, x - y = 2}, [y, x], BackSubstitution = FALSE)![]()
solve({x^2 + y = 1, x - y = 2}, {x, y})![]()
Если MuPAD не может выразить результата как набора списков, то BackSubstitution не имеет никакого эффекта:
solve({x^2 + y = 1, x - y = 2}, [y, x],
BackSubstitution = FALSE, MaxDegree = 1)![]()
Если вход содержит числа с плавающей запятой, MuPAD использует символьный решатель solve, и затем вызывает функцию float для полученного решения:
solve(x^3 + 3.0*x + 1, x)
![]()
Если символьному решателю не удается решить такое уравнение или систему, MuPAD вызывает числовой решатель numeric::solve:
solve({sin(x) + 1/2*cos(sqrt(2)*y) = 1, cos(x) + sin(y) = 0.1}, {x, y})![]()
Числовой решатель может возвратить неполный набор решений. Для получения дополнительной информации смотрите страницу справки numeric::solve.
Если числитель содержит учтенный полином с кратностью, больше, чем 1, решения могут дать нули в знаменателе:
solve((x - 1)^2/(x - 1) = 0, x)
![]()
Чтобы устранить эти решения, расширьте числитель:
f := expand((x - 1)^2): solve(f/(x - 1) = 0, x)
![]()
Можно использовать функцию solve, чтобы решить диофантовые уравнения. Например, решите следующее линейное диофантовое уравнение:
S := solve(30*x + 56*y = 2, [x, y], Domain = Z_)
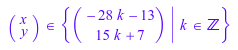
Можно использовать функцию solve, чтобы решить уравнение, данное в форме членств. Например, решите следующее уравнение:
solve(x^2 in Z_, x)
![]()
Можно решить уравнение с символьными параметрами, таким образом найдя его общее решение. Затем можно оценить решение для каких-то конкретных значений параметров или построить решение относительно значений параметров.
Решите это уравнение:
S := solve(x^5 + a = 1, x, Real)
![]()
Постройте результат для значений -10 < a < 10:
plot(S, a = -10..10)
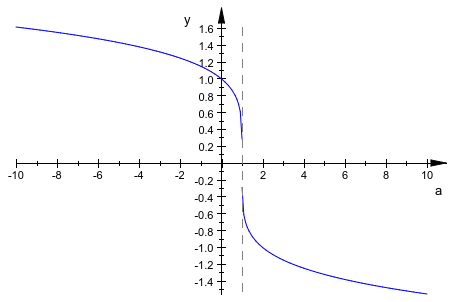
Оцените результат для a = 5 с помощью оператора | или его функциональная форма evalAt:
S | a = 5
![]()
Аппроксимируйте результат со значением с плавающей точкой с помощью float:
float(%)
![]()
|
Одно уравнение или неравенство типа |
|
Неопределенное, для которого вы решаете уравнение, неравенство системы: идентификатор или индексируемый идентификатор |
| |
|
Непустой набор или список indeterminates, для которого вы решаете уравнение, неравенство или систему |
|
Набор, список, массив или таблица уравнений, неравенств, арифметических выражений или любой комбинации этих объектов. Решатель рассматривает выражения как уравнения без правой стороны. (Внутренне, решатель принимает, что правая сторона равна 0.) |
|
Обыкновенное дифференциальное уравнение: объект типа |
|
Уравнение повторения: объект типа |
|
Опция, заданная как Не используйте явные формулы, которые вовлекают радикалов при решении полиномиальных уравнений степени, больше, чем Эта опция включает и отключает использование явных формул для корней полиномов. Эта опция не влияет на другие методы, такие как факторизация. Для полиномиальных уравнений данная максимальная степень Когда вы решаете пятую часть - или полиномиальное уравнение высшего порядка, решатель может не мочь возвратить решение явным образом. В целом нет никаких явных выражений для корней полиномов степеней выше, чем 4. Установка опции |
|
Опция, заданная как Включите или отключите обратные подстановки при решении алгебраических систем. Значением
|
|
При использовании этой опции Решатель игнорирует эту опцию, если вход не является многочленным выражением или уравнением, или если решение имеет тип |
|
Возвратите набор векторов при решении системы уравнений для списка переменных. |
|
При использовании этой опции решатель возвращает только одно решение. Решатель возвращает это решение как набор с одним элементом. Если уравнение не имеет решения, решатель возвращает пустое множество. Если решатель не может найти решение и не может доказать, что решения не существуют, это отвечает на неразрешенный символьный звонок к Также можно использовать эту опцию, чтобы решить уравнения больше чем для одной переменной. В этом случае решатель возвращает набор, который содержит один список. Эта вложенная структура представляет вектор решения. |
|
Опция, заданная как Возвратите набор всех решений, которые являются элементами Можно решить уравнение или систему по следующим областям:
Подмножество Можно перегрузить решатель для пользовательских областей путем добавления метода Синтаксисом вызова для Вы не можете решить уравнения и системы больше чем в одной переменной по областям. |
|
Включайте решения, которые не сопоставимы со свойствами переменной |
|
Возвратите только решения, для которых каждое подвыражение При использовании этой опции решатель принимает, что каждое подвыражение, независимое от Когда вы используете эту опцию, MuPAD ограничивает область каждой функции к вещественным числам. Например, это не поддерживает логарифмы отрицательных чисел. Для всех возвращенных решений Эта опция особенно полезна для решения неравенств. Неравенства содержат только, когда обе стороны представляют действительные значения. Эта опция не влияет на некоторые системы. |
|
Если решение требует анализа случая, игнорируйте регистры, для которых один или несколько параметров в уравнении, как предполагается, являются элементом сравнительно маленького набора (например, с этой опцией, MuPAD может проигнорировать членство в фиксированном конечном множестве или наборе целых чисел При использовании этой опции решатель пытается сократить количество ответвлений в кусочных объектах. MuPAD находит уравнения и членства в сравнительно маленьких наборах. Во-первых, MuPAD пытается доказать такие уравнения и членства при помощи механизма свойства. Если механизм свойства доказывает уравнение, или членство верно, MuPAD сохраняет тот оператор. В противном случае MuPAD может заменить тот оператор на значение |
|
Примените чисто алгебраические упрощения в выражениях и уравнениях. При использовании этой опции решатель применяет следующие правила к выражениям с обеих сторон уравнения:
Используя эту опцию, можно получить простые решения для уравнений, для которых прямой вызов решателя возвращает сложные результаты. Обратите внимание на то, что с этой опцией решатель не проверяет правильность и полноту результата. Смотрите Пример 8 и Пример 9. |
|
Не преобразовывайте уравнение к эквивалентной системе уравнений. Эта опция уменьшает время выполнения. При использовании этой опции решатель не может решить некоторые уравнения. Эта опция не позволяет решателю заменять уравнение на эквивалентную систему уравнений. Как правило, MuPAD заменяет уравнение эквивалентной системой уравнений при решении уравнений с вложенными корнями. Решение получившейся системы может быть медленным. Используйте эту опцию, чтобы улучшать производительность решателя. Когда вы используете |
|
Подавите все предупреждающие сообщения. |
Если x является идентификатором, solve(eq, x) возвращает объект, который представляет математический набор (см. раздел “Details”). Если x является набором или списком, или если вы не используете x, вызов solve возвращает набор списков. Каждый список состоит из уравнений. Левая сторона каждого уравнения является одной из переменных, для которых вы решаете уравнение, неравенство системы. В этом случае solve также может возвратить выражение формы x in S, где x является списком переменных, и S является набором векторов. Когда вы решаете систему, предоставляющую список переменных и опцию VectorFormat, решатель возвращает набор векторов.
eq