Dom:: FractionПоле частей интегральной области
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Dom::Fraction(R)Dom::Fraction(R)(r)Dom::Fraction(R) создает область, которая представляет поле частей
интегрального доменного R.
Элемент доменного Dom::Fraction(R) имеет два операнда, числитель и знаменатель.
Если Dom::Fraction(R) имеет аксиому Ax::canonicalRep (см. ниже), знаменатели имеют модульную нормальную форму и gcds отмены числителей и знаменателей.
Доменный Dom::Fraction(Dom::Integer) представляет поле рациональных чисел. Но созданной областью не является доменный Dom::Rational, потому что это использует различное представление своих элементов. Арифметика в Dom::Rational намного более эффективна, чем это находится в Dom::Fraction(Dom::Integer).
Если r является рациональным выражением, то элемент поля частей Dom::Fraction(R) создается путем прохождения через операндов r и преобразования каждого операнда в элемент R. Результатом этого процесса является r в форме
, где x и y являются элементами R. Если R имеет Cat::GcdDomain, то x и y являются взаимно-простыми.
Если один из операндов не может быть преобразован в доменный R, сообщение об ошибке выпущено.
Мы задаем поле рациональных функций по rationals:
F := Dom::Fraction(Dom::Polynomial(Dom::Rational))
и создайте элемент F:
a := F(y/(x - 1) + 1/(x + 1))
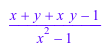
Чтобы вычислить с такими элементами используют стандартные арифметические операторы:
2*a, 1/a, a*a
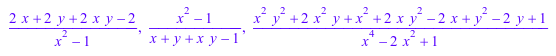
Некоторые системные функции перегружаются для элементов областей, сгенерированных Dom::Fraction, таких как diff, numer или denom (см. описание соответствующих методов "diff", "numer" и "denom" выше).
Например, чтобы дифференцировать дробный a относительно x войдите:
diff(a, x)
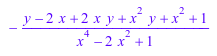
Если вы знаете переменные заранее, то использование доменного Dom::DistributedPolynomial приводит к более эффективной арифметике рациональных функций:
Fxy := Dom::Fraction( Dom::DistributedPolynomial([x, y], Dom::Rational) )
b := Fxy(y/(x - 1) + 1/(x + 1)): b^3
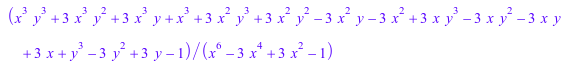
Мы создаем поле рациональных чисел как поле частей целых чисел, т.е.
:
Q := Dom::Fraction(Dom::Integer): Q(1/3)
domtype(%)
Другим представлением ℚ в MuPAD® является доменный Dom::Rational, где rationals имеют области ядра DOM_INT и DOM_RAT. Поэтому намного более эффективно работать с Dom::Rational, чем с Dom::Fraction(Dom::Integer).
|
Интегральная область, т.е. область категории |
|
Рациональное выражение или элемент |
| "характеристика" | характеристика |
| "coeffRing" | интегральный доменный |
| "один" | тот поля частей |
| "нуль" | нуль поля частей |
_divide — Разделите две части_divide(x, y)
Этот метод перегружает функциональный _divide для частей, т.е. можно использовать его в форме x / y или в функциональном обозначении: _divide(x, y).
_invert — Инвертируйте часть_invert(r)
Этот метод перегружает функциональный _invert для частей, т.е. можно использовать его в форме 1/r или r^(-1), или в функциональном обозначении: _invert(r).
_less — Меньше отношение_less(q, r)
Реализация обеспечивается, только если R является упорядоченным множеством, т.е. областью категории Cat::OrderedSet.
Этот метод перегружает функциональный _less для частей, т.е. можно использовать его в форме q < r, или в функциональном обозначении: _less(q, r).
_mult — Мультиплие фракционируется частями или рациональными выражениями_mult(q, r)
Если q не имеет доменного типа Dom::Fraction(R), это рассматривается как рациональное выражение, которое преобразовано в часть по R и умножено с q. Если преобразование перестало работать, FAIL возвращен.
То же самое применяется к r.
Этот метод также обрабатывает больше чем два аргумента. В этом случае список аргументов является splitted в две части той же длины, которая оба умножаются с функциональным _mult. Два результата умножаются снова с _mult, результат которого затем возвращен.
Этот метод перегружает функциональный _mult для частей, т.е. можно использовать его в форме q * r или в функциональном обозначении: _mult(q, r).
_negate — Инвертируйте часть_negate(r)
Этот метод перегружает функциональный _negate для частей, т.е. можно использовать его в форме -r или в функциональном обозначении: _negate(r).
_power — Целочисленная степень части_power(r, n)
Этот метод перегружает функциональный _power для частей, т.е. можно использовать его в форме r^n или в функциональном обозначении: _power(r, n).
плюс Добавьте части_plus(q, r, …)
Если один из аргументов не имеет доменного типа Dom::Fraction(R), то FAIL возвращен.
Этот метод перегружает функциональный _plus для частей, т.е. можно использовать его в форме q + r или в функциональном обозначении: _plus(q, r).
D Дифференциальный операторD(r)
Реализация обеспечивается, только если R является звонком частного дифференциала, т.е. областью категории Cat::PartialDifferentialRing.
Этот метод перегружает оператор D для частей, т.е. можно использовать его в форме D(r).
denom — Знаменатель частиdenom(r)
Этот метод перегружает функциональный denom для частей, т.е. можно использовать его в форме denom(r).
diff Дифференцирование частейdiff(r, u)
Этот метод перегружает функциональный diff для частей, т.е. можно использовать его в форме diff(r, u).
Реализация обеспечивается, только если R является звонком частного дифференциала, т.е. областью категории Cat::PartialDifferentialRing.
equal — Протестируйте на равенстве частейequal(q, r)
фактор Разложите на множители числитель и знаменатель частиfactor(r)
Факторы u, r 1, …, r n является частями типа Dom::Fraction(R), экспоненты e 1, …, e, n является целыми числами.
Системная функция factor используется, чтобы выполнить факторизацию числителя и знаменатель r.
Этот метод перегружает функциональный factor для частей, т.е. можно использовать его в форме factor(r).
intmult — Целочисленное кратное частьintmult(r, n)
iszero — Протестируйте на нульiszero(r)
Элемент поля Dom::Fraction(R) является нулем, если его числитель является нулевым элементом R. Обратите внимание на то, что может быть больше чем одно представление нулевого элемента, если R не имеет Ax::canonicalRep.
Этот метод перегружает функциональный iszero для частей, т.е. можно использовать его в форме iszero(r).
numer — Числитель частиnumer(r)
Этот метод перегружает функциональный numer для частей, т.е. можно использовать его в форме numer(r).
random — Случайная дробная генерацияrandom()
Возвращающаяся часть нормирована (см. методы "normalize" и "normalizePrime".
convert_to — Дробное преобразованиеconvert_to(r, T)
Если преобразование перестало работать, FAIL возвращен.
Преобразование успешно выполняется, если T является одной из следующих областей: Dom::Expression или Dom::ArithmeticalExpression.
Используйте функциональный expr, чтобы преобразовать r в объект области ядра (см. ниже).
retract — Сокращение, чтобы основывать областьretract(r)
normalize — Нормализация частейnormalize(x, y)
Нормализация означает удалять GCD x и y. Следовательно, R должен иметь категорию Cat::GcdDomain. В противном случае нормализация не может быть выполнена, и результатом этого метода является часть
.
normalizePrime — Нормализация частей по интегральным областям с GCDnormalizePrime(x, y)
В звонках категории Cat::GcdDomain элементы приняты, чтобы быть относительно главными. Следовательно, нет никакой потребности нормировать часть
.
В звонках не категории Cat::GcdDomain, не может быть выполнена нормализация элементов, и результатом этого метода является часть
.