laguerreLПолиномы Лагерра и функция L
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
laguerreL(n, x) laguerreL(n, a, x)
laguerreL(n, a, x) представляет функцию L Лагерра. Когда n является неотрицательным целым числом, это - классический полином Лагерра степени n.
Функция L Лагерра задана с точки зрения гипергеометрических функций
![]() .
.
Для неотрицательных целочисленных значений n функция возвращает классические (обобщенные) полиномы, которые являются ортогональными относительно скалярного произведения![]() . В частности:
. В частности:
 .
.
Функция L Лагерра не четко определена для всех значений параметров n и a, потому что определенные ограничения на параметры существуют в определении гипергеометрических функций. Если функция L Лагерра не задана для конкретного парного n и a, вызов laguerreL(n, a, x) возвращается 0 или выдает ошибку сообщение.
Вызовы laguerre(n, x) и laguerre(n, 0, x) эквивалентны.
Если n является неотрицательным целым числом, функциональный laguerreL возвращает явную форму соответствующего полинома Лагерра. Специальные значения![]() реализованы для произвольных значений n и a. Если n является отрицательным целым числом, и a является числовым значением нецелого числа, удовлетворяющим a ≥ - n, то функциональный
реализованы для произвольных значений n и a. Если n является отрицательным целым числом, и a является числовым значением нецелого числа, удовлетворяющим a ≥ - n, то функциональный laguerreL возвращается 0. Если n является отрицательным целым числом, и a является целым числом, удовлетворяющим a <-n, то функция возвращает явное выражение, заданное отражательным правилом
![]() .
.
Если все аргументы являются числовыми, и по крайней мере один из аргументов является числом с плавающей запятой, то laguerreL(x) возвращает число с плавающей запятой. Для всех других аргументов laguerreL(n, a, x) возвращает символьный вызов функции.
Когда названо аргументами с плавающей точкой, функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Можно вызвать функцию laguerreL с точными и символьными аргументами:
laguerreL(2, a, x), laguerreL(-2, -2, PI)
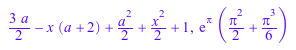
Если первый аргумент является неотрицательным целым числом, функция возвращает полином:
laguerreL(3, x)
![]()
laguerreL(3, a, x)
![]()
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
laguerreL(2, 3, 4.0), laguerreL(5.0, sqrt(2), PI)
![]()
laguerreL(1 + I, 1.0), laguerreL(-2.0, exp(I))
![]()
Функция Лагерра не задана для всех значений параметров:
laguerreL(-5/2, -3/2, x)
Error: Function 'laguerreL' not supported for parameter values '-5/2' and '-3/2'. [laguerreL]
Системные функции, такие как diff, float, limit и series обрабатывают выражения, включающие laguerreL:
diff(laguerreL(n, a, x), x, x, x), float(laguerreL(2, 3, sqrt(PI)))
![]()
limit(laguerreL(3, 4, x^2/(1+x)), x = infinity)
![]()
limit(laguerreL(4, 3, x^2/(1+x)), x = infinity)
![]()
series(laguerreL(n, a, x), x = 0, 3)

series(laguerreL(3/2, x), x = infinity, 3)

|
Арифметическое выражение.
x