orthpoly:: jacobiПолиномы Якоби
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
orthpoly::jacobi(n, a, b, x)
orthpoly::jacobi(n,a,b,x) вычисляет значение n-th степень полином Якоби с параметрами a и b в точке x.
Оценка для действительных значений с плавающей точкой x от интервала [-1.0, 1.0] численно стабилен. Смотрите Пример 2.
Многочленные выражения возвращены, если идентификаторы или индексируемые идентификаторы заданы:
orthpoly::jacobi(2, a, b, x)
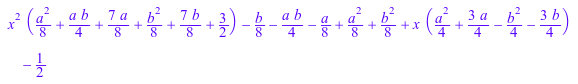
orthpoly::jacobi(3, 4, 5, x[1])
![]()
Используя арифметические выражения, как введено, возвращены “значения” этих полиномов:
orthpoly::jacobi(2, 4, 1, 3+2*I)
![]()
orthpoly::jacobi(2, 0, I, exp(x[1] + 2))
![]()
“Арифметические выражения” включают числа:
orthpoly::jacobi(2, 1/2, -1/2, sqrt(2)), orthpoly::jacobi(3, 2, 5, 8 + I), orthpoly::jacobi(1000, 1, 2, 0.3);
![]()
Если степень полинома является переменной или выражением, то orthpoly::jacobi возвращает себя символически:
orthpoly::jacobi(n, a, b, x)
![]()
Если значение с плавающей точкой желаемо, то прямой вызов такой как
orthpoly::jacobi(100, 1/2, 3/2, 0.9)
![]()
является соответствующим и приводит к правильному результату. Не нужно оценивать символьный полином в значении с плавающей точкой, потому что это может быть численно нестабильно:
P100 := orthpoly::jacobi(100, 1/2, 3/2, x):
evalp(P100, x = 0.9)
![]()
Этот результат вызывается числовым округлением. Также с увеличенным DIGITS только несколько ведущих цифр правильны:
DIGITS := 30: evalp(P100, x = 0.9)
![]()
delete P100, DIGITS:
|
Неотрицательное целое число или арифметическое выражение, представляющее неотрицательное целое число: степень полинома. |
|
Арифметические выражения. |
|
Неопределенное или арифметическое выражение. Неопределенным является любой идентификатор (доменного типа |
Значение полинома Якоби в точке x возвращено как арифметическое выражение. Если n является арифметическим выражением, то orthpoly::jacobi возвращает себя символически.
Полиномы Якоби даны формулой рекурсии

с c i = i + a + b и
![]() .
.
Для фиксированного действительного a> - 1, b> - 1 полиномы Якоби являются ортогональными на интервале [-1, 1] относительно функции веса w (x) = (1 - x) a (1 + x) b.
Для специальных значений параметров a b полиномы Якоби связаны с Полиномами лежандра
![]() ,
,
к Полиномам Чебышева первого вида
![]() ,
,
к Полиномам Чебышева второго вида
![]() ,
,
и к полиномам Gegenbauer, соответственно:
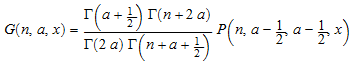 .
.