`график::`

Круговые и эллиптические дуги в 2D

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

plot::Arc2d(r, <[c_x, c_y]>, <α .. β>, <a = a_min .. a_max>, options)
plot::Arc2d([r₁, r₂], <[c_x, c_y]>, <α .. β>, <a = a_min .. a_max>, options)

Описание

plot::Arc2d(r, [x, y], α .. β ) создает круговую дугу с радиусом r и центр (x, y) с углом в полярных координатах между α и β.

_{plot::Arc2d([r1, r2], [x, y], α .. β )} создает соответствующую эллиптическую дугу с полуосями _r1, _r2.

Угол точки на дуге является обычным углом в полярных координатах к положительному x - ось, известная от полярных координат. Это измеряется в радианах.

Если вы не задаете область значений для угла в полярных координатах, plot::Arc3d создает полный круг/эллипс.

Если вы не задаете центральную точку, plot::Arc3d создает дугу с центром [0,0].

Атрибуты

Атрибут	Цель	Значение по умолчанию
`AffectViewingBox`	влияние объектов на `ViewingBox` сцены	`TRUE`
`Angle`	угол поворота	0
`AngleEnd`	конец угловой области значений	`PI/2`
`AngleBegin`	начните угловой области значений	0
`AngleRange`	угловая область значений	`0`.. `PI/2`
`AntiAliased`	сглаженные строки и точки?	`TRUE`
`Center`	центр объектов, центр вращения	[0, 0]
`CenterX`	центр объектов, центр вращения, x-компонент	0
`CenterY`	центр объектов, центр вращения, y-компонент	0
`Closed`	откройтесь или закрытые полигоны	`FALSE`
`Filled`	заполненные или прозрачные области и поверхности	`FALSE`
`FillColor`	цвет областей и поверхностей	`RGB::Red`
`FillPattern`	тип заполнения области	`DiagonalLines`
`Frames`	количество кадров в анимации	50
`Legend`	делает запись легенды
`LegendText`	короткий объяснительный текст для легенды
`LegendEntry`	добавить этот объект в легенду?	`FALSE`
`LineColor`	цвет строк	`RGB::Blue`
`LineWidth`	ширина строк	0.35
`LineStyle`	тело, подчеркнутые штриховой линией или пунктирные линии?	`Solid`
`LinesVisible`	видимость строк	`TRUE`
`Name`	имя объекта графика (для браузера и легенды)
`ParameterEnd`	закончите значение параметра анимации
`ParameterName`	имя параметра анимации
`ParameterBegin`	начальное значение параметра анимации
`ParameterRange`	область значений параметра анимации
`SemiAxes`	полу оси замещающих знаков и ellipsods	[1, 1]
`SemiAxisX`	сначала полу ось замещающих знаков и ellipsods	1
`SemiAxisY`	вторая полу ось замещающих знаков и ellipsods	1
`TimeEnd`	время окончания анимации	10.0
`TimeBegin`	время начала анимации	0.0
`TimeRange`	оперативный промежуток анимации	0.0 .. 10.0
`Title`	объектный заголовок
`TitleFont`	шрифт объектных заголовков	[`" sans-serif "`, `11`]
`TitlePosition`	положение объектных заголовков
`TitleAlignment`	выравнивание по горизонтали заголовков w.r.t. их координаты	`Center`
`TitlePositionX`	положение объектных заголовков, x компонент
`TitlePositionY`	положение объектных заголовков, y компонент
`Visible`	видимость	`TRUE`
`VisibleAfter`	объект, видимый после этой временной стоимости
`VisibleBefore`	объект, видимый до этой временной стоимости
`VisibleFromTo`	объект, видимый в это время, располагается
`VisibleAfterEnd`	объект, видимый после его законченного времени анимации?	`TRUE`
`VisibleBeforeBegin`	объект, видимый перед его временем анимации, запускается?	`TRUE`

Примеры

Пример 1

Дуга является сегментом круга:

circle := plot::Circle2d(3, [0, 0]):
arc := plot::Arc2d(3, [0, 0], 0 .. PI/4, LineColor = RGB::Red,
                   LineWidth = 1.5*unit::mm):
plot(circle, arc)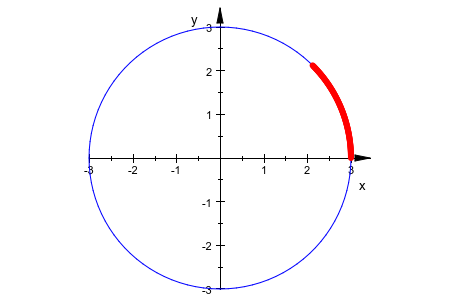

delete circle, arc:

Пример 2

Центру дуги можно дать как второй аргумент к plot::Arc2d:

arc1 := plot::Arc2d(3, [1, 3], 0..PI/2, Closed = TRUE):
arc2 := plot::Arc2d(3, [3, 1], -PI ..0, Closed = TRUE):
plot(arc1, arc2)

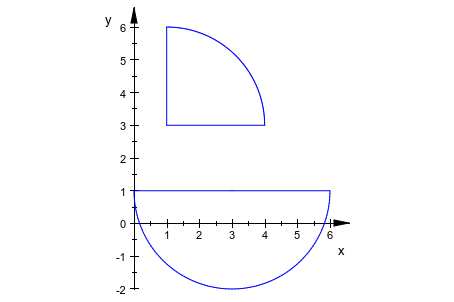
Центр доступен как атрибут Center объекта дуги. Измените центр второй дуги:

arc2::Center := [1, 3]:
plot(arc1, arc2)

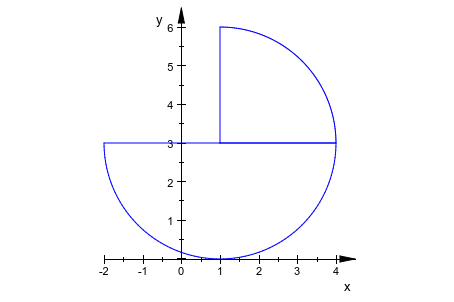
delete arc1, arc2:

Пример 3

Заполненная дуга является сегментом круга, как часть круга:

plot(plot::Arc2d(1, -PI/4..PI/4, Filled = TRUE))

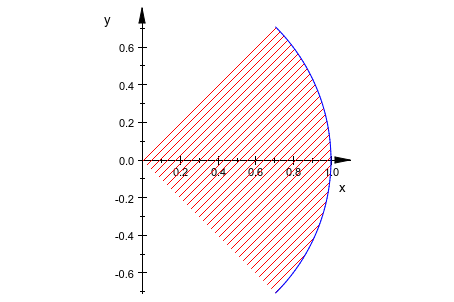
plot(plot::Arc2d(1, -PI/4..PI/4, Filled = TRUE, Closed = TRUE))

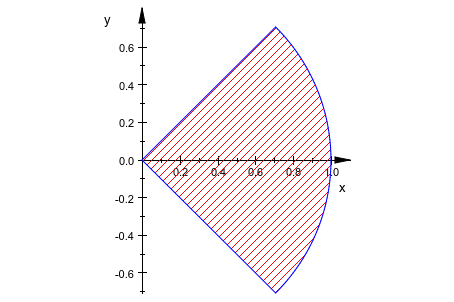
plot(plot::Arc2d(1, -PI/4..PI/4, Filled = TRUE,
                 FillPattern = Solid, LinesVisible = FALSE),
                 AxesInFront = TRUE)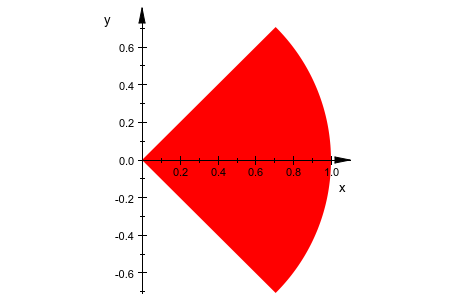

Пример 4

Когда дали список двух радиусов, plot::Arc2d чертит сегмент эллипса с соответствующими полуосями:

arc1 := plot::Arc2d([2, 1], 0 .. PI, Color = RGB::Blue):
arc2 := plot::Arc2d([2, 1], -PI .. 0, Color = RGB::Red):
plot(arc1, arc2)

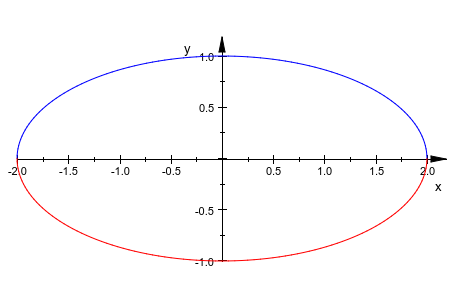
delete arc1, arc2:

Пример 5

Чтобы построить или анимировать сегменты наклоненного эллипса, используйте атрибут Angle:

arc:= [1, 1], [0, 0], PI/4..PI/2, Filled, Closed, FillPattern=Solid:
plot(plot::Arc2d(arc, Angle=a+0,      a=0..2*PI, FillColor=RGB::Red),
     plot::Arc2d(arc, Angle=a+1/2*PI, a=0..2*PI, FillColor=RGB::Green),
     plot::Arc2d(arc, Angle=a+PI,     a=0..2*PI, FillColor=RGB::Yellow),
     plot::Arc2d(arc, Angle=a+3/2*PI, a=0..2*PI, FillColor=RGB::Blue))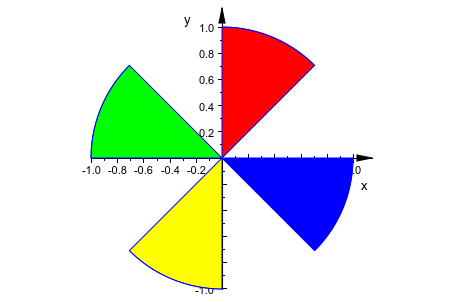

delete arc:

Пример 6

Создайте следующие анимированные 2D дуги:

plot(plot::Arc2d(1, a .. PI, a = 0..PI))

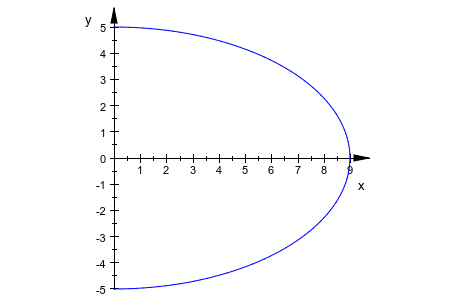
plot(plot::Arc2d([1 + a^2/2, 1 + a], -PI/2 .. PI/2, a = 0..4))

Параметры

`r`	Радиус круга. Это должно быть действительным численным значением или арифметическим выражением параметра анимации `a`. `r` эквивалентен атрибутам `SemiAxisX`, `SemiAxisY`.
`_r1`, `_r2`	Полуоси эллиптической дуги. Они должны быть действительными численными значениями или арифметическими выражениями параметра анимации `a`. `_r1`, `_r2` эквивалентен атрибутам `SemiAxisX`, `SemiAxisY`.
`_cx`, `_cy`	Центральная точка. Координаты `_cx`, `_cy` должен быть действительными численными значениями или арифметическими выражениями параметра анимации `a`. Если никакой центр не задан, дуга, сосредоточенная в начале координат, создается. `_cx`, `_cy` эквивалентен атрибуту `Center`.
α .. β	Угловая область значений в радианах: `α` и `β` должны быть действительными численными значениями или арифметическими выражениями параметра анимации `a`. Областью значений по умолчанию является `0 .. 2*PI`. `α`.. `β` эквивалентен атрибуту `AngleRange`.
`a`	Параметр анимации, заданный как `a` `_{= amin..amax}`, где `_amin` является начальным значением параметров и `_amax`, является итоговым значением параметров.

Документация