`Angle`

Угол поворота

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.

Сводные данные значения

Дополнительный

Выражение MuPAD^®

Графические примитивы

Объекты	Угловые значения по умолчанию
`plot::Arc2d`, `plot::Arc3d`, `plot::Prism`, `plot::Pyramid`, `plot::Rotate2d`, `plot::Rotate3d`	0

Описание

Angle определяет угол поворота в объектах преобразования типа plot::Rotate2d и plot::Rotate3d, соответственно, и другие графические объекты. Угол должен быть задан в радианах.

В 2D направление вращения является встречными мудрыми часами. Используйте отрицательные углы, чтобы вращать мудрые часы.

В 3D вращение реализовано после “правила правой руки”: Расширьте ползунок правой руки и изогните пальцы. Когда точки ползунка в направление оси вращения, ваши кончики пальцев указывают на направление вращения. Используйте отрицательные углы, чтобы вращаться в противоположном направлении.

Примеры

Пример 1

Прямоугольники типа plot::Rectangle всегда параллельны осям координат. Чтобы иметь один с различной ориентацией, мы должны вращать его:

r0 := plot::Rectangle(0..2, 1..3):
r1 := plot::Rotate2d(r0, Center = [1, 2], Angle = PI/6)

Как вы видите в выводе выше, вращать объект содержит вращаемый объект и действует как группирующееся построение. Это означает, что мы только должны построить r1, чтобы видеть вращаемый объект:

plot(r1)

Графический вывод и r0 и r1 приводит к графику, показывающему вращаемый прямоугольник вместе с невращаемым:

plot(r0, r1)

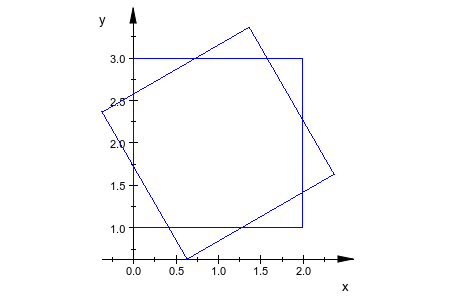
delete r0, r1:

Пример 2

Используя plot::Rotate2d, мы строим несколько копий графика функций, вращаемого под различными углами:

f := plot::Function2d(sin(x^3)/(x^2+1), x = -5..5, Mesh = 300):
plot(plot::Rotate2d(f, Angle = PI/11*a) $ a = 0..10):

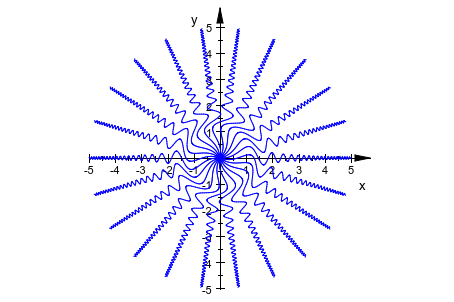
delete f:

Пример 3

Угол поворота может быть анимирован. Мы используем анимированный объект plot::Rotate2d вращать квадрат вокруг центра, который проходит круг вокруг источника:

p := plot::Point2d([cos(a), sin(a)], a = 0..2*PI,
                   Frames = 100):
r := plot::Rotate2d(plot::Rectangle(0..2, -1..1), Angle = a,
                    Center = [0, 0], a = 0..2*PI):
q := plot::Rotate2d(r, Angle = 4*a, Center = [cos(a), sin(a)],
                    a = 0..2*PI, Frames = 200):
plot(p, q)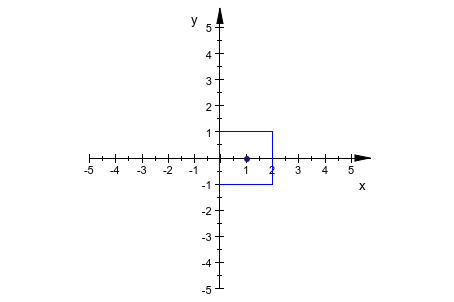

delete p, r, q:

Пример 4

Это - 3D аналог Примера 1. Поля типа plot::Box всегда параллельны осям координат. Чтобы иметь один с различной ориентацией, мы должны вращать его:

b0 := plot::Box(0..2, 1..3, 2..3):
b1 := plot::Rotate3d(b0, Center = [1, 2, 2.5],
                     Axis = [1, 1, 1], Angle = PI/5)

plot(b0, b1)

delete b0, b1:

Пример 5

Некоторые графические объекты, например, plot::Arc2d и plot::Pyramid, также принимают угол поворота:

arc:= [3, 1], [0, 0], -PI/4..PI/4, Filled:
plot(
  plot::Arc2d(arc, Angle=0,      FillColor=RGB::Red),
  plot::Arc2d(arc, Angle=1/2*PI, FillColor=RGB::Green),
  plot::Arc2d(arc, Angle=PI,     FillColor=RGB::Yellow),
  plot::Arc2d(arc, Angle=3/2*PI, FillColor=RGB::Blue)
)

plot(plot::Pyramid(1/2, Angle=0),
     plot::Pyramid(1/2, Angle=PI/4, FillColor2=RGB::Yellow))

delete arc:

Документация