график::3D параллелограммы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
plot::Parallelogram3d([cx, cy, cz], [ux, uy, uz], [vx, vy, vz], <a = amin .. amax>, options)
plot::Parallelogram3d(c, u, v) задает 3D параллелограмм
с центром
и векторами
,
охватывая плоскость параллелограмма. Это - прямоугольник со сторонами длины
,
если векторы
и
являются ортогональными.
plot::Parallelogram3d создает 3D параллелограмм с центром
= [cx, cy, cz] и стороны, данные векторами
= [2 ux, 2 uy, 2 uz] и
= [2 vx, 2 vy, 2 vz]. Углами параллелограмма дают
, 
и
:
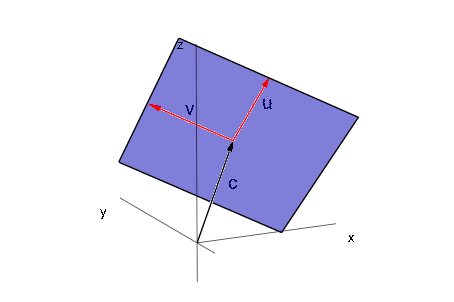
По умолчанию область параллелограмма заполнена цветом, заданным атрибутом Color или, эквивалентно, FillColor. С Filled = FALSE, только границы параллелограмма видимы. Их цвет выбран атрибутом LineColor.
Также центру и векторам охвата можно дать как векторы.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox сцены | TRUE |
Center | центр объектов, центр вращения | [0, 0, 0] |
CenterX | центр объектов, центр вращения, x-компонент | 0 |
CenterY | центр объектов, центр вращения, y-компонент | 0 |
CenterZ | центр объектов, центр вращения, z-компонент | 0 |
Color | основной цвет | RGB::LightBlue |
Filled | заполненные или прозрачные области и поверхности | TRUE |
FillColor | цвет областей и поверхностей | RGB::LightBlue |
FillColor2 | второй цвет областей и поверхностей для цветных смешений | RGB::CornflowerBlue |
FillColorType | типы заполнения поверхности | Flat |
FillColorDirection | направление цветовых переходов на поверхностях | [0, 0, 1] |
FillColorDirectionX | x-компонент направления цветовых переходов на поверхностях | 0 |
FillColorDirectionY | y-компонент направления цветовых переходов на поверхностях | 0 |
FillColorDirectionZ | z-компонент направления цветовых переходов на поверхностях | 1 |
Frames | количество кадров в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет строк | RGB::Black.[0.25] |
LineWidth | ширина строк | 0.35 |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость строк | TRUE |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
Tangent1 | первые параллелограммы охвата вектора | [0, 1, 0] |
Tangent2 | вторые параллелограммы охвата вектора | [1, 0, 0] |
Tangent1X | первые параллелограммы охвата вектора, x компонент | 0 |
Tangent1Y | первые параллелограммы охвата вектора, y компонент | 1 |
Tangent2X | вторые параллелограммы охвата вектора, x компонент | 1 |
Tangent1Z | первые параллелограммы охвата вектора, z компонент | 0 |
Tangent2Y | вторые параллелограммы охвата вектора, y компонент | 0 |
Tangent2Z | вторые параллелограммы охвата вектора, z компонент | 0 |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 .. 10.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11] |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
TitlePositionZ | положение объектных заголовков, z компонент | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
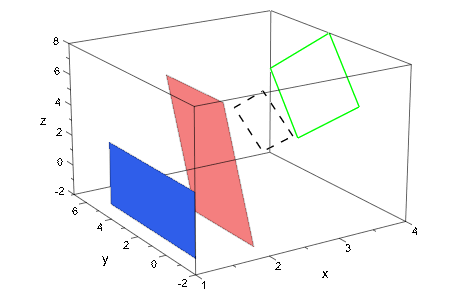
Постройте несколько прямоугольников и параллелограммов с помощью различных стилей презентации:
plot(plot::Parallelogram3d([1, 1, 1], [0, 0, 2], [0, 3, 0]),
plot::Parallelogram3d([2, 2, 2], [0, 1, 4], [0, 2, 0],
FillColor = RGB::Red.[0.5]),
plot::Parallelogram3d([3, 3, 3], [0, 1, 1], [0, 1, -1],
Filled = FALSE, LineStyle = Dashed,
LineColor = RGB::Black),
plot::Parallelogram3d([4, 4, 4], [0, 1, 2], [0, 2, -2],
Filled = FALSE, LineColor = RGB::Green)
):
Используйте plot::Parallelogram3d, чтобы визуализировать плоскости касательной поверхности. Первая поверхность является графиком функционального f (x, y) = x 2 + y 2. В точке (x, y, f (x, y)) на графике, векторы касательной в x и направлении y даны (1, 0, 2 x) и (0, 1, 2 y), соответственно. После нормализации к длине 0.4, они приводят к векторам касательной u, v, используемый в конструкции плоскостей касательной:
f := (x, y) -> x^2 + y^2:
c:= (x, y) -> [x, y, f(x, y)]:
u := (x, y) -> [0.4/sqrt(1+4*x^2), 0, 0.8*x/sqrt(1+4*x^2)]:
v := (x, y) -> [0, 0.4/sqrt(1+4*y^2), 0.8*y/sqrt(1+4*y^2)]:
plot(plot::Function3d(f(x, y), x = -1..1, y = -1..1),
plot::Parallelogram3d(c(0, 0), u(0, 0), v(0, 0),
Color = RGB::Grey.[0.5]),
plot::Parallelogram3d(c(0, -1), u(0, -1), v(0, -1),
Color = RGB::Grey.[0.5]),
plot::Parallelogram3d(c(-1, 0), u(-1, 0), v(-1, 0),
Color = RGB::Grey.[0.5]),
plot::Parallelogram3d(c(-1/2, -1/2), u(-1/2, -1/2),
v(-1/2, -1/2),
Color = RGB::Grey.[0.5])):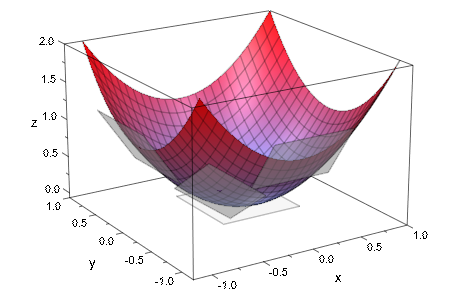
Вторая поверхность является сферой, параметризованной сферическими координатами p и t (полярный и угол азимута). В точке (x (p, t), y (p, t), z (p, t)) на сфере, векторы касательной в p и направлении t даны дифференцированием x, y, z относительно p и t, соответственно. После нормализации к длине 0.5, они приводят к векторам касательной u, v, используемый в конструкции плоскостей касательной:
x := (p, t) -> cos(p)*sin(t):
y := (p, t) -> sin(p)*sin(t):
z := (p, t) -> cos(t):
c := (p, t) -> [x(p, t), y(p, t), z(p, t)]:
u := (p, t) -> [-0.5*sin(p), 0.5*cos(p), 0]:
v := (p, t) -> [0.5*cos(p)*cos(t), 0.5*sin(p)*cos(t),
-0.5*sin(t)]:
plot(plot::Surface(c(p, t), p = 0..2*PI, t = 0..PI),
plot::Point3d(c(0, 0), Color = RGB::Black),
plot::Parallelogram3d(c(0, 0), u(0, 0), v(0, 0),
Color = RGB::Grey.[0.5]),
plot::Point3d(c(-3*PI/4, PI/4), Color = RGB::Black),
plot::Parallelogram3d(c(-3*PI/4, PI/4),
u(-3*PI/4, PI/4),
v(-3*PI/4, PI/4),
Color = RGB::Grey.[0.5]),
plot::Point3d(c(-PI/2, PI/3), Color = RGB::Black),
plot::Parallelogram3d(c(-PI/2, PI/3),
u(-PI/2, PI/3),
v(-PI/2, PI/3),
Color = RGB::Grey.[0.5]),
plot::Point3d(c(PI, PI/2), Color = RGB::Black),
plot::Parallelogram3d(c(PI, PI/2),
u(PI, PI/2),
v(PI, PI/2),
Color = RGB::Grey.[0.5]),
Scaling = Constrained):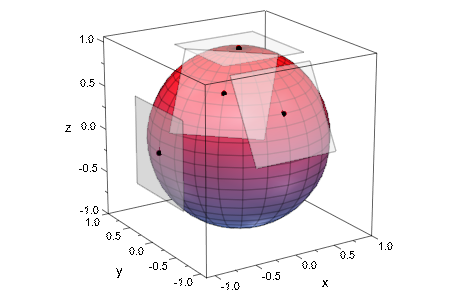
delete f, c, u, v, x, y, z:
|
Координаты центра: действительные численные значения или выражения параметра анимации
|
|
Компоненты первого вектора, охватывающего параллелограмм: действительные численные значения или выражения параметра анимации
|
|
Компоненты второго вектора, охватывающего параллелограмм: действительные численные значения или выражения параметра анимации
|
|
Параметр анимации, заданный как |