график::График плотности
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
plot::Density(f,x = xmin .. xmax,y = ymin .. ymax, <a = amin .. amax>,options) plot::Density(A, <x = xmin .. xmax, y = ymin .. ymax>, <a = amin .. amax>,options) plot::Density(L, <x = xmin .. xmax, y = ymin .. ymax>, <a = amin .. amax>,options)
plot::Density(f(x, y), x = `x_{min}`..`x_{max}` , y = `y_{min}`..`y_{max}` ) генерирует регулярную 2D сетку прямоугольного расширения от левого нижнего угла (xmin, ymin) к правому верхнему углу (xmax, ymax). Прямоугольник со средней точкой (x, y) окрашен согласно цветовой схеме на основе значения “плотности” f (x, y).
plot::Density служит для визуализации 3D данных (x, y, f (x, y)) 2D графиком. Примерно разговор, это соответствует цветному 3D функциональному графику функции плотности f (x, y) просматриваемый сверху. Однако в отличие от 3D функционального графика, plot::Density не использует сглаженную интерполяцию (“штриховка”) цвета между смежными прямоугольниками.
Если данные о плотности обеспечиваются массивом или матричным A или списком L, количество прямоугольников в графике плотности дано автоматически форматом A или L, соответственно.
Если данные о плотности даны выражением или функциональным f, атрибут Mesh = подачи [m, n] для уведомления plot::Density создать сетку m ×n прямоугольники. Также можно установить XMesh = m, YMesh = n.
С FillColorType по умолчанию = Dichromatic, прямоугольник со значением плотности f (x, y) в средней точке (x, y) окрашен с цветом
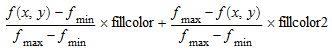 ,
,
где![]() минимальные/максимальные значения плотности в графике и
минимальные/максимальные значения плотности в графике и fillcolor, fillcolor2, значения RGB атрибутов FillColor и FillColor2, соответственно. Таким образом fillcolor указывает на значения высокой плотности, тогда как fillcolor2 указывает на низкие значения плотности.
Если f min = f max, плоская окраска с fillcolor используется.
С FillColorType = Monochrome, прямоугольник со значением плотности f (x, y) в средней точке (x, y) окрашен с цветом
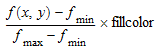 .
.
Пользователь может задать функцию цвета заливки через FillColorFunction = mycolorfunction, чтобы заменить окраску плотности, описанную выше. Процедура mycolorfunction будет вызвана аргументами
mycolorfunction(x, y, f(x, y, a ) a ),
где (x, y) средние точки прямоугольников, и a является параметром анимации. Функция управления цветом должна возвратить значение цвета RGBa или RGB.
Когда значения плотности заданы массивом или матричным A, низкие индексы соответствуют левому нижнему углу графики. Высокие индексы соответствуют правому верхнему углу.
Массивы/матрицы не должны быть индексированы от 1. Например,
A = array( `i_{min}` .. `i_{max}` , `j_{min}` .. `j_{max}` , [..density values..])
приводит к графическому массиву с
XMesh = jmax - jmin + 1, YMesh = imax - imin + 1.
Если никакая область значений графика `x_{min}` .. `x_{max}`, `y_{min}` .. `y_{max}` задан,
xmin = jmin - 1, xmax = jmax, ymin = imin - 1, ymax = imax
используется.
Когда значения плотности заданы списком списков L, первые записи в списке соответствуют левому нижнему углу графики. Последние записи соответствуют правому верхнему углу.
Если никакая область значений графика `x_{min}` .. `x_{max}`, `y_{min}` .. `y_{max}` задан,
xmin = 0, xmax = m, ymin = 0, ymax = n
используется, где n является длиной L, и m является (общей) длиной подсписков в L. Все подсписки (“строки”) должны иметь ту же длину.
Анимации инициированы путем определения области значений a = `a_{min}` .. `a_{max}` для параметра a, который отличается от переменных x, y. Таким образом, в анимациях, оба области значений x = `x_{min}` .. `x_{max}`, y = `y_{min}` .. `y_{max}`, а также область значений анимации a = `a_{min}` .. `a_{max}` должен быть задан.
Связанная стандартная программа графика plot::Raster обеспечивает схожую функциональность. Однако plot::Raster не использует автоматическую цветовую схему на основе значений плотности. Пользователь должен обеспечить RGB или значения RGBa вместо этого.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox сцены | TRUE |
AntiAliased | сглаженные строки и точки? | FALSE |
Color | основной цвет | RGB::Red |
DensityData | значения плотности для графика плотности | |
DensityFunction | функция плотности для графика плотности | |
FillColor | цвет областей и поверхностей | RGB::Red |
FillColor2 | второй цвет областей и поверхностей для цветных смешений | RGB::CornflowerBlue |
FillColorType | типы заполнения поверхности | Dichromatic |
FillColorFunction | функциональная область / поверхностная окраска | |
Frames | количество кадров в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет строк | RGB::Blue |
LineWidth | ширина строк | 0.35 |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость строк | FALSE |
Mesh | количество точек выборки | [25, 25] |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 .. 10.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11] |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
XMax | окончательное значение параметра “x” | |
XMesh | количество точек выборки для параметра “x” | 25 |
XMin | начальное значение параметра “x” | |
XName | имя параметра “x” | |
XRange | область значений параметра “x” | |
YMax | окончательное значение параметра “y” | |
YMesh | количество точек выборки для параметра “y” | 25 |
YMin | начальное значение параметра “y” | |
YName | имя параметра “y” | |
YRange | область значений параметра “y” |
Мы генерируем график плотности:
p := plot::Density(cos(x^2 + y^2), x = -3..3, y = -2..2,
Mesh = [60, 40]):Объект графика представляется:
plot(p, Axes = Frame):
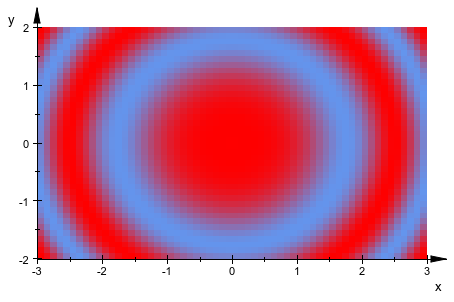
Это превращается в черно-белую графику, когда подходящие цвета заданы:
plot(plot::Scene2d(p, FillColor = RGB::White,
FillColor2 = RGB::Black),
plot::Scene2d(p, FillColor = RGB::Black,
FillColor2 = RGB::White),
Width = 120*unit::mm, Height = 45*unit::mm,
Layout = Horizontal, Axes = Frame):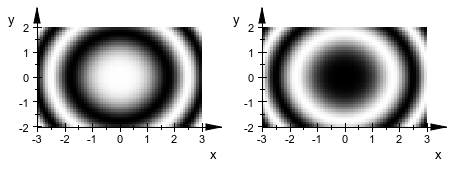
delete p:
Мы демонстрируем использование пользовательской функции управления цветом:
mycolor := proc(x, y, f)
begin
if f >= 2/3 then RGB::Red
elif f >= 1/3 then RGB::Orange;
elif f >= 0 then RGB::Yellow;
elif f >= -1/3 then RGB::BlueLight;
elif f >= -2/3 then RGB::Blue;
else RGB::SlateBlueDark;
end_if;
end_proc:
plot(plot::Density(cos(x^2 + y^2), x = -3..3, y = -2..2,
Mesh = [60, 40],
FillColorFunction = mycolor),
Axes = Frame):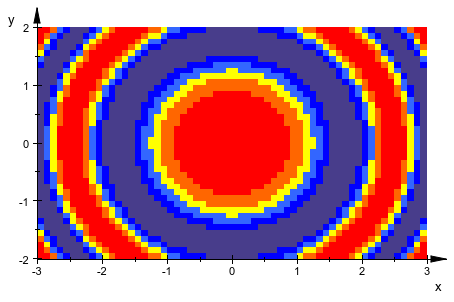
delete mycolor:
В этом примере мы демонстрируем, как plot::Density может использоваться, чтобы отобразить серые данные на графике из внешнего источника. Примите, существует внешний текстовый файл PortableGrayMap Norton.pgm, содержащий данные такой как
P2
240 180
255
249 237 228 231 245 218 229 195 ...
P2, указывающий, что это - текстовый файл PGM. Вторая строка содержит пиксельную ширину и пиксельную высоту изображения. Номер 255 в третьей строке является шкалой следующих уровней яркости.
Остающиеся данные состоят из целых чисел между 0 (черными цветами) и 255 (белыми) цветами, каждый представляющий уровень яркости пикселя (строка строкой).
Мы импортируем текстовые данные через import::readdata:
graydata := import::readdata("Norton.pgm", NonNested):Это - длинный список всех элементов данных в файле. Мы извлекаем эти 4 элемента в первых трех строках:
[magicvalue, xmesh, ymesh, maxgray] := graydata[1..4]
![]()
Мы удаляем заголовок из пиксельных данных. (Если существуют комментарии в файле PGM, они должны быть удалены, также).
for i from 1 to 4 do delete graydata[1]; end_for:
Мы преобразовываем простой список данных к вложенному списку, содержащему серые данные строк как подсписки. (Вызов level не действительно необходим, но это значительно ускоряет преобразование на интерактивном уровне.)
L := level([graydata[(i - 1)*xmesh + 1 .. i*xmesh] $ i=1..ymesh], 1):
Этот список может быть передан plot::Density:
plot(plot::Density(L, FillColor = RGB::White,
FillColor2 = RGB::Black),
Width = 80*unit::mm, Height = 60*unit::mm):
Изображение перевернуто, потому что файлы PGM хранят строку пиксельных данных строкой в обычном порядке чтения начиная с левого верхнего угла изображения. Стандартная программа MuPAD® plot::Density, однако, следует за математической ориентацией осей координат, т.е. первым пиксельным значением, интерпретирована как левый нижний угол изображения. Мы должны переупорядочить строки в списке graydata через revert:
plot(plot::Density(revert(L), FillColor = RGB::White,
FillColor2= RGB::Black),
Width = 80*unit::mm, Height = 60*unit::mm):
Стандартные программы import::readbitmap и plot::Raster обеспечивают альтернативный способ импортировать и отобразить растровое изображение. Смотрите страницу справки графика:: Растр для примеров. Это, однако, берет больше памяти, потому что растровые данные импортированы как значения цвета RGB, тогда как только значения плотности (серые данные) необходимы для plot::Density.
delete graydata, magicvalue, xmesh, ymesh, maxgray, i, L:
Множество Мандельброта является одним из самых известных фракталов. Это возникает при считании итерации z n + 1 = z n 2 + c, z 0 = 0 в комплексной плоскости. Для достаточно больших значений |c | комплексного параметра c, последовательность z n отличается к бесконечности; это сходится для достаточно маленьких значений |c |. Контур области тех значений c, которые приводят к расхождению z n, особенно интересен: эта граница является высоко сложной и фрактальной природы.
В частности, известно, что серия z n отличается к бесконечности, каждый раз, когда одно из выполнения итерации удовлетворяет |zn |> 2. Этот факт используется следующей процедурой f как останавливающийся критерий. Возвращаемое значение предоставляет информацию, сколько выполняет итерации z 0, …, z n, который это берет, чтобы сбежать из области |z | ≤ 2 из (потенциальной) сходимости. Эти данные должны использоваться, чтобы окрасить комплексную плоскость c (т.е. (x, y) плоскостью) графиком плотности:
f := proc(x, y)
local c, z, n;
begin
c := x + I*y:
z := 0.0:
for n from 0 to 100 do
z := z^2 + c:
if abs(z) > 2 then
break;
end_if;
end_for:
if n < 70 then
n mod 5;
else n - 70;
end_if;
end_proc:В зависимости от вашего компьютера могут занять время следующие вычисления. На очень быстрой машине можно увеличить следующие значения xmesh, ymesh. Это израсходует более вычислительное время, но приведет к лучшим графическим результатам:
xmesh := 100: ymesh := 100:
Следующая область в x-y плоскость должна быть рассмотрена:
xmin[1] := -2.0: xmax[1] := 0.5: ymin[1] := -1.2: ymax[1] := 1.2:
Область xmin 1 ≤ x ≤ xmax 1, ymin 1 ≤ y ≤ ymax 1 разделен на xmesh ×ymesh прямоугольники. Каждый прямоугольник окрашен графиком плотности согласно “временам Escape”, вычисленным процедурой f. Эта процедура может быть передана непосредственно plot::Density:
p1 := plot::Density(f, x = xmin[1].. xmax[1],
y = ymin[1] .. ymax[1],
Mesh = [xmesh, ymesh],
FillColor = RGB::Black,
FillColor2 = RGB::Red):Кроме того, прямоугольник производится, который указывает на область, которая должна быть увеличена в следующем:
xmin[2] := -0.24: xmax[2] := -0.01:
ymin[2] := 0.63: ymax[2] := 0.92:
r1 := plot::Rectangle(xmin[2] .. xmax[2], ymin[2] .. ymax[2],
LineColor = RGB::White):plot(p1, r1):

Значения плотности взрыва не вычисляются непосредственно plot::Density. Они вычисляются отдельно и хранятся в массиве A:
dx := (xmax[2] - xmin[2])/xmesh:
dy := (ymax[2] - ymin[2])/ymesh:
A := array(1..ymesh, 1..xmesh,
[[f(xmin[2]+ (j - 1/2)*dx, ymin[2] + (i - 1/2)*dy)
$ j = 1..xmesh] $ i = 1..ymesh]):
p2 := plot::Density(A, x = xmin[2] .. xmax[2], y = ymin[2] .. ymax[2],
FillColor = RGB::Black, FillColor2 = RGB::Red):Кроме того, дальнейший прямоугольник производится, чтобы указать на видимую область, которая будет аварийно завершена lateron:
xmin[3] := -0.045: xmax[3] := -0.015:
ymin[3] := 0.773: ymax[3] := 0.815:
r2 := plot::Rectangle(xmin[3] .. xmax[3], ymin[3] .. ymax[3],
LineColor = RGB::White):plot(p2, r2):
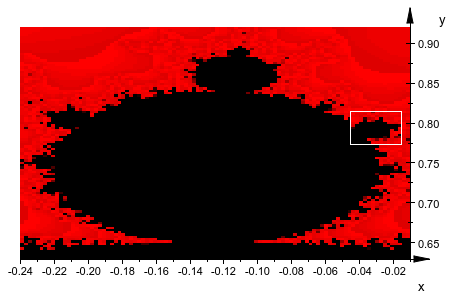
Значения плотности следующего взрыва снова вычисляются отдельно и хранятся во вложенном списке L:
dx := (xmax[3] - xmin[3])/xmesh:
dy := (ymax[3] - ymin[3])/ymesh:
L := [[f(xmin[3] + (j - 1/2)*dx, ymin[3] + (i - 1/2)*dy)
$ j= 1..xmesh] $ i = 1..ymesh]:
p3 := plot::Density(L, x = xmin[3] .. xmax[3], y = ymin[3] .. ymax[3],
FillColor = RGB::Black, FillColor2 = RGB::Red):plot(p3):
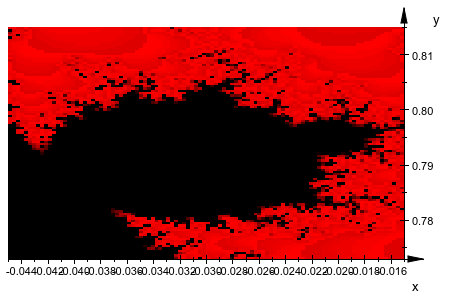
Объекты плотности состоят в том, чтобы быть помещены в одну графику. Это состоит из Множества Мандельброта, p1, как вычислено выше и из модификаций плотности строит p2 и p3. Переопределяя атрибуты XRange, YRange, мы перемещаем p2, p3 к местам в x-y плоскость, где они не перекрываются p1. Обратите внимание на то, что это не изменяет графическое содержимое p2, p3, потому что это дано по условию A и L, соответственно, которые остаются неизменными. (Если бы области значений были изменены в p1, другой вызов plot p1 вызвал бы процедуру f в различных точках плоскости, приводящей к различной графике.)
p2::XRange := 0.60 .. 1.60: p2::YRange := 0.05 .. 1.15: p3::XRange := 0.60 .. 1.60: p3::YRange := -1.15 .. -0.05:
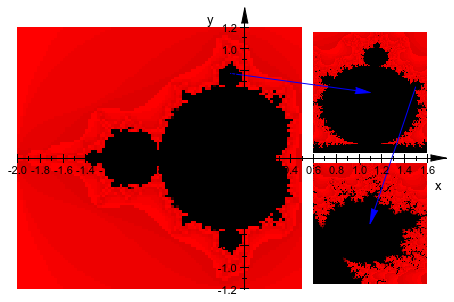
Множество Мандельброта и эти два взрыва помещаются в одну сцену. Кроме того, некоторые стрелки добавляются, чтобы указать на источник взрывов. Обратите внимание на то, что довольно важно здесь, чтобы стрелки были переданы команде plot после графиков плотности. В противном случае они были бы скрыты графиками плотности: графические объекты нарисованы в упорядоченном расположении, в котором они передаются plot:
plot(p1, p2, p3,
plot::Arrow2d([(xmin[2] + xmax[2])/2,
(ymin[2] + ymax[2])/2],
[(p2::XMin + p2::XMax)/2,
(p2::YMin + p2::YMax)/2],
LineColor = RGB::Blue),
plot::Arrow2d([1.50, 0.65],
[(p3::XMin + p3::XMax)/2,
(p3::YMin + p3::YMax)/2],
LineColor = RGB::Blue)
):
delete f, xmesh, ymesh, xmin, xmax, ymin, ymax,
dx, dy, p1, p2, p3, r1, r2, A, L:
|
Значения плотности: арифметическое выражение в 2 переменных x, y и параметре анимации a. Также процедура, которая принимает 2 входных параметра x, y или 3 входных параметра x, y, a и возвращает действительное значение плотности.
|
|
Имя горизонтальной переменной: идентификатор или индексируемый идентификатор.
|
|
Область значений горизонтальной переменной: |
|
Имя вертикальной переменной: идентификатор или индексируемый идентификатор.
|
|
Область значений вертикальной переменной: |
|
Массив доменного типа
|
|
Список списков числовых значений плотности или выражений параметра анимации a. Каждый подсписок L представляет строку графического массива. Количество подсписков в L приводит к значению атрибута
|
|
Параметр анимации, заданный как |