Документация

Интегрируйте пользовательские функции в MuPAD

MuPAD^® обеспечивает множество инструментов для обработки встроенных математических функций, таких как sin, cos, exp, и так далее. Эти инструменты реализуют математические свойства этих функций. Типичными примерами является подпрограмма преобразования float, функция дифференцирования diff или функция expand, которую вы используете, чтобы управлять выражениями:

float(sin(1));
diff(sin(x), x, x, x);
expand(sin(x + 1))

Можно сказать, что математическое знание о встроенных функциях распределяется по нескольким системным функциям: float знает, как вычислить числовые приближения синусоидальной функции, diff знает производную синусоидальной функции, и expand знает теоремы сложения тригонометрических функций.

Когда вы реализуете свою собственную функцию, можно интегрировать ее в систему MuPAD, информируя другие функции, как работать с этой новой функцией правильно. Если новая функция состоит только из встроенных функций MuPAD, то вы не должны делать дополнительные шаги. Все функции MuPAD взаимодействуют правильно с новой функцией:

f := x -> (x*sin(x)):
diff(f(x), x)

Однако, если вы реализуете функцию, которая не состоит из стандартных объектов MuPAD (например, новая специальная функция), необходимо распределить знание о математическом значении новой функции к стандартным функциям MuPAD, таким как diff, expand, float, и так далее. Эта дополнительная задача необходима для интеграции новой функции с остальной частью системы. Например, вы можете хотеть дифференцировать выражение, которое содержит и новую функцию и некоторые встроенные функции, и такое дифференцирование только возможно через стандартную программу дифференцирования MuPAD. Поэтому эта стандартная программа должна знать, как обработать новый символ.

Функциональные среды использования MuPAD (область вводят DOM_FUNC_ENV) интегрировать функции в систему. Функциональная среда хранит специальные функциональные атрибуты (slots) во внутренней таблице. Каждый раз, когда сверхзагружаемая системная функция, такая как diff, expand, или float, сталкивается с объектом типа DOM_FUNC_ENV, это ищет функциональную среду соответствующий слот. Если системная функция находит соответствующий слот, она вызывает тот слот и возвращает значение, произведенное слотом. Все встроенные функции MuPAD реализованы как функциональные среды:

domtype(sin), domtype(exp)

Можно вызвать функциональную среду, когда вы вызвали бы любую функцию MuPAD или процедуру:

sin(1.7), exp(1.0)

Предположим, что вы реализуете полные функции эллиптического интеграла первого и второго вида, K(z) и E(z). Эти функции появляются в различных контекстах, таких как вычисление периметра замещающего знака, гравитационного или электростатического потенциала универсального звонка и вероятности, что случайный обход в трех измерениях когда-либо проходит источник. Эллиптические интегралы имеют следующие специальные значения:

, E (1) = 1.

MuPAD предоставляет встроенным функциям ellipticE и ellipticK для вычисления этих эллиптических интегралов. Однако можно реализовать собственные функции для той же задачи. Например, запишите процедурам ellipE и ellipK. Эти процедуры задают значения эллиптических интегралов для специальных значений x. Для всех других значений аргументов значения эллиптических интегралов неизвестны, и процедуры возвращают символьные выражения ellipE(x) и ellipK(x). Используйте procname, чтобы возвратить символьные выражения:

ellipE :=
proc(x) begin
  if x = 0 then PI/2
  elif x = 1 then 1
  else procname(x) end_if
end_proc:

ellipK :=
proc(x) begin
  if x = 0 then PI/2
  elif x = 1/2 then 8*PI^(3/2)/gamma(-1/4)^2
  elif x = -1 then gamma(1/4)^2/4/sqrt(2*PI)
  else procname(x) end_if
end_proc:

ellipE и ellipK возвращают специальные значения для конкретных аргументов. Для всех других аргументов они возвращают символьные выражения:

ellipE(0), ellipE(1/2),
ellipK(12/17), ellipK(x^2 + 1)

Первые производные этих эллиптических интегралов следующие:

, .

Стандартная функция дифференцирования MuPAD diff не знает об этих правилах. Поэтому попытка дифференцировать ellipE и ellipK просто возвращает символьные обозначения производных:

diff(ellipE(x), x),
diff(ellipK(x), x)

Чтобы заставить diff работать с новыми функциями, создайте функциональные среды из процедур ellipE и ellipK. Кроме того, функциональные среды позволяют вам управлять внешним видом символьных вызовов функции в выходных параметрах.

Функциональная среда состоит из трех операндов.

Чтобы создать функциональные среды, используйте funcenv. Например, создайте функциональные среды ellipE и ellipK. Используйте второй аргумент, чтобы указать, что символьные вызовы ellipE и ellipK должны появиться как E и K выходные параметры:

output_E := f -> hold(E)(op(f)):
ellipE := funcenv(ellipE, output_E):

output_K := f -> hold(K)(op(f)):
ellipK := funcenv(ellipK, output_K):

Несмотря на то, что ellipE и ellipK являются теперь функциональными средами, можно вызвать их, когда вы вызвали бы любую другую функцию MuPAD:

ellipE(0), ellipE(1/2),
ellipK(12/17), ellipK(x^2+1)

Третий аргумент funcenv является таблицей функциональных атрибутов. Это говорит системные функции (такие как float, diff, expand, и так далее), как обработать символьные вызовы формы ellipE(x) и ellipK(x). Можно обновить эту таблицу, задающую правила для новой функции. Например, задайте новые правила дифференцирования путем присвоения соответствующих процедур слоту diff функциональных сред:

ellipE::diff :=
proc(f,x)
local z;
begin
z := op(f);
(ellipE(z) - ellipK(z))/(2*z) * diff(z, x)
end_proc:

ellipK::diff :=
proc(f,x)
local z;
begin
z := op(f);
(ellipE(z) - (1-z)*ellipK(z))/
(2*(1-z)*z) * diff(z, x)
end_proc:

Теперь, каждый раз, когда f = ellipE(z) и z зависят от x, вызов, diff(f, x) использует процедуру, присвоенную ellipE::diff:

diff(ellipE(z), z);
diff(ellipE(y(x)), x);
diff(ellipE(x*sin(x)), x)

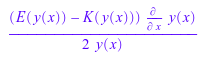
Новая стандартная программа дифференцирования также находит производные высшего порядка:

diff(ellipE(x), x, x)

Поскольку функция taylor внутренне вызывает diff, новая стандартная программа дифференцирования также позволяет вам вычислить Разложения Тейлора эллиптических интегралов:

taylor(ellipK(x), x = 0, 6)

Если производная функции содержит саму функцию, стандартная программа интегрирования имеет хороший шанс нахождения символьных интегралов после того, как вы реализуете атрибуты diff. Например, int теперь вычисляет следующие интегралы:

int(ellipE(x), x)

int(ellipK(x), x)