taylorВычислите расширение Ряда Тейлора
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
taylor(f,x, <order>, <mode>) taylor(f,x = x0, <order>, <mode>) taylor(f,x, <AbsoluteOrder = order>) taylor(f,x = x0, <AbsoluteOrder = order>) taylor(f,x, <RelativeOrder = order>) taylor(f,x = x0, <RelativeOrder = order>)
taylor(f, x = x0) вычисляет первые сроки Ряда Тейлора f относительно переменной x вокруг точки x0.
Если taylor находит соответствующий Ряд Тейлора, результатом является последовательное расширение доменного типа Series::Puiseux. Используйте expr, чтобы преобразовать его в арифметическое выражение доменного типа DOM_EXPR. Смотрите Пример 1.
Если Ряд Тейлора не существует или если taylor не может найти его, то taylor выдает ошибку. Смотрите Пример 2 и Пример 3.
Математически, расширение, вычисленное taylor, допустимо в некотором открытом диске вокруг точки расширения в комплексной плоскости.
Если x0 является complexInfinity, то расширение вокруг комплексной бесконечности, т.е. Северный полюс Римановой сферы, вычисляется. Если x0 является infinity или -infinity, направленное последовательное расширение, допустимое вдоль вещественной оси, вычисляется.
Такое расширение вычисляется можно следующим образом: серийная переменная x в f заменяется
. Затем направленное последовательное расширение в u = 0 справа вычисляется. Если x0 = complexInfinity, то неориентированное расширение вокруг u = 0 вычисляется. Наконец,
заменен в результате.
Математически, результатом расширения вокруг complexInfinity или ± infinity является степенной ряд в
. Смотрите Пример 4.
С режимом по умолчанию RelativeOrder количеством требуемых условий для расширения является order, если задано. Если никакой order не задан, значение переменной окружения используемый ORDER. Можно изменить значение по умолчанию 6 путем присвоения нового значения ORDER.
Количество условий считается от самого низкого термина степени на для конечных точек расширения, и от самого высокого термина степени на для расширений вокруг бесконечности, т.е. “order” должен рассматриваться как “относительный порядок усечения”.
Если AbsoluteOrder задан, order представляет порядок усечения ряда (т.е. степень x в Большом О сроке).
taylor использует более общую серийную функцию series, чтобы вычислить Разложение Тейлора. Смотрите соответствующую страницу справки для series для получения дополнительной информации о параметрах и структуре данных расширения Ряда Тейлора.
Функция чувствительна к переменной окружения ORDER, который определяет количество по умолчанию условий в последовательных вычислениях.
Вычислите Ряд Тейлора вокруг точки 0 по умолчанию:
s := taylor(exp(x^2), x)
Результат taylor имеет следующий доменный тип:
domtype(s)
Если вы применяете функциональный expr к ряду, результатом является арифметическое выражение без термина порядка:
expr(s)
domtype(%)
delete s:
Расширение Ряда Тейлора
приблизительно x = 1 не существует. Поэтому taylor выдает ошибку:
taylor(1/(x^2 - 1), x = 1)
Error: Unable to compute Taylor expansion of '1/(x^2 - 1)'. Try 'series' for a more general expansion. [taylor]
Вызовите series, чтобы вычислить более общее последовательное расширение. Расширение Лорана действительно существует:
series(1/(x^2 - 1), x = 1)
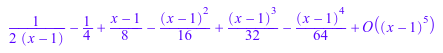
Если taylor не может найти расширение Ряда Тейлора, он также выдает ошибку.
taylor(psi(1/x), x = 0)
Error: Unable to compute Taylor expansion of 'psi(1/x)'. Try 'series' with the 'Left', 'Right', or 'Real' option for a more general expansion. [taylor]
Вызовите series с дополнительным аргументом. В этом случае series возвращает более общий тип расширения. В случаях, где series не может найти последовательное расширение, он возвращает символьный вызов функции.
series(psi(1/x), x = 0, Right)
Это - пример направленного Разложения Тейлора вдоль вещественной оси вокруг infinity:
taylor(exp(1/x), x = infinity)
На самом деле это - даже неориентированное расширение:
taylor(exp(1/x), x = complexInfinity)
|
Арифметическое выражение, представляющее функцию в |
| |
|
Точка расширения: арифметическое выражение. Также выражения, включающие Если не заданный, точка 0 расширения по умолчанию используется. |
|
Порядок усечения (в сочетании с |
|
Один из флагов |
|
С этим флагом целочисленное значение |
|
С этим флагом, экспонентами |
Объект доменного типа Series::Puiseux или символьное выражение типа "taylor".
f
O | Series::Puiseux | Type::Series | asympt | diff | limit | mtaylor | series