Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
При решении линейной системы символьных уравнений общий решатель возвращает набор решений:
S := solve([x + y = 1, 3*x - 2*y = 5], [x, y])
Присвойте отдельные решения переменных с помощью оператора evalAt или |:
xSol := x | S[1]; ySol := y | S[1];
Функциональный linsolve возвращает список решений:
linsolve([x + y = 1, 3*x - 2*y = 5], [x, y])
Если существует больше неизвестных, чем независимые уравнения в системе, linsolve решает систему для первых неизвестных:
linsolve([x + y = a, 3*x - 2*y = b], [x, y, a, b])
Обеспечение неизвестных в различном порядке влияет на решение:
linsolve([x + y = a, 3*x - 2*y = b], [a, b, x, y])
Чтобы утвердить проблему решения системы линейных уравнений в матричной форме, используйте следующие шаги:
Создайте матричный A, содержащий коэффициенты условий линейных уравнений. Каждое уравнение способствует строке в A.
Создайте вектор-столбец
, содержащий правые стороны уравнений.
Матричная форма линейной системы
. При решении системы в матричной форме вы обеспечиваете матричный A и вектор
. Решатель возвращает решения системы как вектор
.
Размерности m×n матрицы коэффициентов задают следующие типы линейных систем.
m = n | Квадратная система | Если детерминант A не является нулем, уникальное решение системы существует. В противном случае система имеет или бесконечно много решений или никакие решения. |
m > n | Сверхрешительная система | Система включает больше уравнений, чем переменные. Система может иметь одно решение, бесконечно много решений или никакие решения. |
m < n | Недоопределенная система | Система включает больше переменных, чем уравнения. Система имеет или бесконечно много решений или никакие решения. |
Чтобы решить линейную систему в матричной форме, используйте команду linalg::matlinsolve. Например, решите следующую систему линейных уравнений:
eqn1 := 2*x + 3*y = 4: eqn2 := 3*x - 2*y = 1:
Чтобы преобразовать систему в матричную форму, используйте команду matrix, чтобы создать матрицу коэффициентов и вектора, содержащего правые стороны уравнений:
A := matrix([[2, 3],[3, -2]]); b := matrix([4, 1])
Как ярлык для преобразования системы линейных уравнений к матричной форме, используйте linalg::expr2Matrix:
Ab := linalg::expr2Matrix([eqn1, eqn2], [x,y])
Теперь, используйте linalg::matlinsolve, чтобы решить систему:
linalg::matlinsolve(Ab)
Также разделите матричный Ab в матрицу коэффициентов A и векторный b, содержащий правые стороны уравнений. Используйте linalg::matlinsolve, чтобы решить систему:
A := Ab[1..2, 1..2]: b := Ab[1..2, 3..3]: linalg::matlinsolve(A, b)
Если ваша линейная система первоначально задана матричным уравнением, использование матричной формы, чтобы решить систему более интуитивно. Кроме того, матричная форма удобна для решения уравнений со многими переменными, потому что это старается не создавать символы для этих переменных. Например, следующие матрицы задают линейную систему:
A := linalg::hilbert(10); b := matrix([i^(-2) $ i = 1..10])
Чтобы решить эту систему, используйте linalg::matlinsolve:
linalg::matlinsolve(A, b)
Если ваша система линейных уравнений может быть представлена как специализированная матрица, можно решить систему путем вызова специального решателя. Прямые вызовы специальных решателей часто улучшают производительность вашего кода. MuPAD® предлагает специальные решатели для линейных систем, которые могут быть представлены матрицами следующих типов:
Матрица, данная
, где L является нижней треугольной матрицей и U, является верхней треугольной матрицей (разложение LU матрицы)
Матрица Теплица. Например, следующая матрица является матрицей Теплица:
.
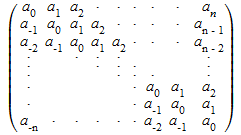Смотрите linalg::toeplitz для определения и деталей.
Матрица Вандермонда. Например, следующая матрица является матрицей Вандермонда::
.
Смотрите linalg::vandermonde для определения и деталей.
Предположим, что вы хотите решить следующую систему, данную матрицей Теплица. Используйте linalg::toeplitz, чтобы задать систему:
T := linalg::toeplitz(3, [0, 2, 5, 3, 0])
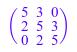
Векторный y задает правые стороны уравнений:
y := matrix([1, 2, 3])
Чтобы решить систему, данную матрицей Теплица, используйте linalg::toeplitzSolve специальный решатель. Этот специальный решатель более эффективен, чем linalg::matlinsolve. Этот решатель принимает вектор или список диагональных элементов t матрицы Теплица вместо самой матрицы Теплица:
t := [0, 2, 5, 3, 0]: x := linalg::toeplitzSolve(t, y)
Для списка специальных решателей, доступных в MuPAD, смотрите Solver Выбора. Для получения информации о функциях линейной алгебры смотрите Линейную алгебру.
Чтобы решить систему нелинейных уравнений символически, используйте общий решатель. Например, решите следующую систему тригонометрических уравнений:
solve({4*cos(x) + 2*cos(y) = 3, 2*sin(x) + sin(y) = 1}, [x, y])
Когда вы используете опцию VectorFormat, решатель возвращает решения как набор векторов. Если вы хотите, чтобы решатель возвратил одно решение в набор, используйте опцию PrincipalValue. Когда вы используете PrincipalValue, решатель все еще возвращает набор, несмотря на то, что тот набор содержит только одно решение:
solve({4*cos(x) + 2*cos(y) = 3, 2*sin(x) + sin(y) = 1},
[x, y], VectorFormat, PrincipalValue)
Можно также аппроксимировать точное символьное решение численно:
float(%)
Если solve не может вычислить явные решения для системы, используйте числовые методы, чтобы аппроксимировать решения. Для нелинейных систем MuPAD предлагает следующие специальные решатели:
Для системы полиномиальных уравнений используйте numeric::polysysroots.
Для произвольной системы уравнений используйте numeric::fsolve.
Предположим, что вы хотите решить следующую систему полиномиальных уравнений:
eqn1 := x^3 + x^2*y - 1: eqn2 := x^2 - y^2 = 1/2:
Общий символьный решатель приводит к результату с точки зрения объекта RootOf:
solve({eqn1, eqn2}, [x, y])
Чтобы аппроксимировать решения системы полиномиальных уравнений численно, используйте специальный решатель numeric::polysysroots:
numeric::polysysroots({eqn1, eqn2}, [x, y])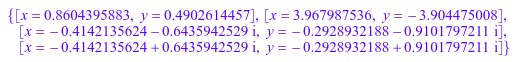
Предположим, что вы хотите решить следующую систему уравнений:
eqn1 := sin(a) - cos(b) + a*b: eqn2 := (sin(a) + cos(b))^3:
Общий решатель не может найти символьное решение:
solve({eqn1, eqn2}, [a, b])
Для числовых приближений решений нелинейной системы уравнений используйте numeric::fsolve. Числовой решатель возвращает только одно решение:
numeric::fsolve({eqn1, eqn2}, [a, b])
Когда numeric::fsolve находит одно решение, он прекращает искать другие решения.
Когда вы решаете произвольную нелинейную систему численно, нет никакого общего способа найти все решения. Для получения дополнительной информации смотрите уравнения Решения Численно.