числовой::Числовые корни системы полиномиальных уравнений
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
numeric::polysysroots(eqs, <NoWarning>) numeric::polysysroots(eqs,vars, <NoWarning>)
numeric::polysysroots(eqs, ...) возвращает числовые приближения всех действительных и комплексных корней полиномиальной системы уравнений eqs.
Коэффициенты полиномов могут содержать символьные параметры.
Если никакие неизвестные не заданы vars, thennumeric::indets(eqs) используется вместо vars.
В большинстве случаев решение возвращено как набор списков решенных уравнений формы
![]() ,
,
где x 1, x 2, … является неизвестными. Эти упрощенные уравнения должны рассматриваться как ограничения на неизвестные. Например, если неизвестный x 1, скажем, не поднимает в форме x 1 = … в решении, то нет никакого ограничения на это неизвестное, и это - произвольный параметр. Это сохраняется в целом для всех неизвестных, которые не поднимаются на левой стороне решенных уравнений. Cf. Пример 2.
Если никакие явные решения не могут быть вычислены, выражения формы может быть возвращен, где S является набором решения.
Упорядоченное расположение неизвестных в vars определяет упорядоченное расположение решенных уравнений. Если setvars используется, то внутреннее упорядоченное расположение используется.
Если набор решения eqs не конечен, то numeric::polysysroots может возвратить решения с некоторыми неизвестными, остающимися как свободные параметры. В этом случае представление решения зависит от упорядоченного расположения неизвестных! Cf. Пример 3. Далее, если более высокие полиномы степени включены, то numeric::polysysroots может не вычислить корни. Cf. Пример 5. То же самое может произойти, когда eqs содержит символьные параметры.
Можно попробовать numeric::fsolve, чтобы вычислить один числовой корень, если numeric::polysysroots не может вычислить все корни системы. Обратите внимание, однако, что numeric::fsolve не принимает символьные параметры в уравнениях.
Мы рекомендуем использовать numeric::polyroots, чтобы вычислить все корни одного одномерного полинома с числовыми коэффициентами.
numeric::polysysroots является гибридной стандартной программой: это вызывает символьный решатель solve(eqs, vars, BackSubstitution = FALSE) и обрабатывает его символьный результат численно. Cf. Пример 4.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Уравнения, выражения, а также объекты DOM_POLY могут использоваться, чтобы задать полиномы:
numeric::polysysroots(x^2 = PI^2, x)
![]()
numeric::polysysroots({x^2 + y^2 - 1, x^2 - y^2 = 1/2}, [x, y])![]()
numeric::polysysroots({poly(x^2 + y + 1), y^2 + x = 1}, [x, y])
Приняты символьные параметры:
numeric::polysysroots(x^2 + y + exp(z), [x, y])
![]()
Возвращенные решения могут содержать некоторые неизвестные, остающиеся как свободные параметры:
numeric::polysysroots({x^2 + y^2 = z}, [x, y, z])![]()
Упорядоченное расположение неизвестных определяет представление решения, если набор решения не конечен. Во-первых, следующее уравнение решено для x, оставив y как свободный параметр:
numeric::polysysroots({x^3 = y^2}, [x, y])
Переупорядочение неизвестных приводит к представлению с x как свободный параметр:
numeric::polysysroots({x^3 = y^2}, [y, x])![]()
Символьный решатель производит решение RootOf следующей системы:
eqs := {y^2 - y = x, x^3 = y^3 + x}:
solve(eqs, BackSubstitution = FALSE)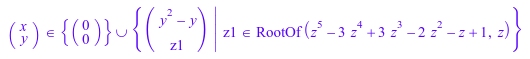
Внутренне, numeric::polysysroots вызывает solve и обрабатывает этот результат численно:
numeric::polysysroots(eqs, [x, y])

delete eqs:
Следующее уравнение решено для первых из заданных неизвестных:
eqs := y^5 - PI*y = x: solve(eqs, [x, y])
![]()
numeric::polysysroots обрабатывает этот вывод численно:
numeric::polysysroots(eqs, [x, y])
![]()
Уравнение решено для y, когда неизвестные переупорядочиваются. Однако никакое простое представление решения не существует, таким образом, объект RootOf возвращен:
solve(eqs, [y, x])
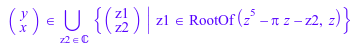
Корни, представленные выражением RootOf, не могут быть вычислены численно, потому что символьный параметр x включен:
numeric::polysysroots(eqs, [y, x])

delete eqs:
|
Полиномиальное уравнение или список, набор, |
|
Неизвестное или список или набор неизвестных. Неизвестные могут быть идентификаторами или индексированными идентификаторами. |
|
По умолчанию корни перепроверяются, автоматически. Предупреждения выданы, если решение, кажется, омрачено некоторой числовой нестабильностью. При использовании этой опции подавлена эта проверка, и никакие предупреждения не будут выданы. |
Набор списков уравнений или выражения формы , где x 1, x 2, … является неизвестными, и S является набором решения.
Набор {[]} содержащий пустой список возвращен, если никакие решения не могут быть вычислены.