Подъем метода для построения вейвлетов

Так называемые вейвлеты первого поколения и масштабирующиеся функции являются двухместными расширениями, и переводит одной функции. Методы Фурье играют ключевую роль в проекте этих вейвлетов. Однако требование, чтобы основание вейвлета состояло из, переводит и расширяет одной функции, налагает некоторые ограничения, которые ограничивают утилиту идеи мультиразрешения в ядре анализа вейвлета.

Утилита методов вейвлета расширена проектом вейвлетов второго поколения через подъем.

Типичные настройки, где перевод и расширение одной функции не могут использоваться, включают:

При разработке вейвлетов на ограниченных областях — Это включает конструкцию вейвлетов через определенный интервал или ограниченную область в более многомерном Евклидово пространстве.
Необходимы взвешенные вейвлеты — В определенных приложениях, таких как решение дифференциальных уравнений с частными производными, вейвлеты, биоортогональные относительно взвешенного скалярного произведения.
Нерегулярно распределенные данные — Во многих реальных приложениях, интервал выборки между выборками данных не равен.

Разработка новых вейвлетов первого поколения требует экспертных знаний в анализе Фурье. Поднимающийся метод, предложенный Sweldens (см. [Swe98] в Ссылках), удаляет необходимость экспертных знаний в анализе Фурье и позволяет вам генерировать бесконечное число дискретных биоортогональных вейвлетов, начинающих с начального. В дополнение к генерации вейвлетов первого поколения с подъемом поднимающийся метод также позволяет вам разработать вейвлеты второго поколения, которые не могут быть разработаны с помощью основанных на Фурье методов. С подъемом можно разработать вейвлеты, которые обращаются к недостаткам вейвлетов первого поколения.

Следующий раздел вводит теорию позади подъема, представляет поднимающиеся функции программного обеспечения Wavelet Toolbox™ и дает два коротких примера:

Для получения дополнительной информации о подъеме см. [Swe98], [Mal98], [StrN96] и [MisMOP03] в Ссылках.

Подъем фона

DWT, реализованный набором фильтров, задан четырьмя фильтрами, как описано в Алгоритме Быстрого преобразования вейвлета (FWT). Два основных свойства интереса

Совершенное свойство реконструкции
Ссылка с “истинными” вейвлетами (как сгенерировать, начинающий с фильтров, ортогональных или биоортогональных основ пробела функций конечной энергии),

Чтобы проиллюстрировать совершенное свойство реконструкции, следующий набор фильтров содержит два фильтра разложения и два фильтра синтеза. Фильтры разложения и синтеза могут составить пару биоортогональных основ или ортогонального основания. Прописные буквы обозначают Z-преобразования фильтров..

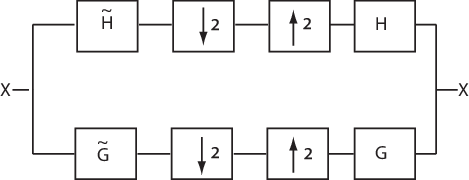
Это приводит к следующим двум условиям для набора фильтров совершенной реконструкции (PR):

$\tilde{H} (z) H (z) + \tilde{G} (z) G (z) = 2 z^{- L + 1}$

$\tilde{H} (- z) H (z) + \tilde{G} (- z) G (z) = 0$

Первое условие обычно (неправильно) называется совершенным условием реконструкции, и вторым является сглаживающееся условие.

Термин ^z–L+1 подразумевает, что совершенная реконструкция достигается до задержки одной выборки меньше, чем длина фильтра, L. Это заканчивается, если аналитические фильтры переключены, чтобы быть причинными.

При подъеме проектов совершенные наборы фильтров реконструкции путем начала с основного характера вейвлета преобразовывают. Вейвлет преобразовывает сборку разреженные представления путем использования корреляции, свойственной от большинства данных о реальном мире. Например, постройте пример потребления электричества за 3-дневный период.

load leleccum;
plot(leleccum)
grid on; axis tight;

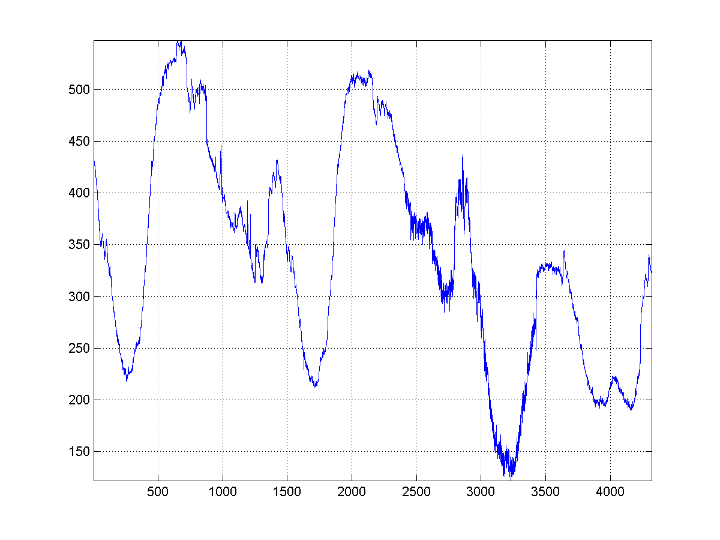
Данные не показывают произвольные изменения от выборки до выборки. Соседние выборки показывают корреляцию. Относительно низкое (высокое) значение в индексе (выборка) n сопоставлено с относительно низким (высоким) значением в индексе n-1 и n+1. Это подразумевает, что, если у вас есть только нечетное или даже выборки от данных, можно предсказать даже или нечетные выборки. Насколько точный ваш прогноз, очевидно, зависит от природы корреляции между смежными выборками и как тесно ваш предиктор аппроксимирует ту корреляцию.

Многофазное представление

Многофазное представление сигнала является важной концепцией в подъеме. Можно просмотреть каждый сигнал как состоящий из фаз, которые состоят из взятия каждого N-th выборка, начинающаяся с некоторого индекса. Например, если вы индексируете временные ряды от n =0 и берете любой демонстрационный запуск в n =0, вы извлекаете ровные выборки. Если вы берете любой демонстрационный запуск с n =1, вы извлекаете нечетные выборки. Это четные и нечетные многофазные компоненты данных. Поскольку ваш шаг между выборками равняется 2, существует только две фазы. Если вы увеличили свой шаг до 4, можно извлечь 4 фазы. Для подъема достаточно сконцентрироваться на четных и нечетных многофазных компонентах. Следующая схема иллюстрирует эту операцию для входного сигнала.

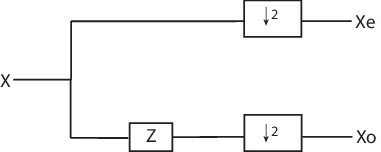
где Z обозначает модульный оператор усовершенствования, и направленная вниз стрелка с номером 2 представляет субдискретизацию два. На языке подъема операция разделения входного сигнала на четные и нечетные компоненты известна как операцию разделения или ленивый вейвлет.

Чтобы понять подъем математически, необходимо понять представление z-области четных и нечетных многофазных компонентов.

Z-преобразование ровного многофазного компонента

$X_{0} (z) = \sum_{n} x (2 n) z^{- n}$

Z-преобразование нечетного многофазного компонента

$X_{1} (z) = \sum_{n} x (2 n + 1) z^{- n}$

Можно записать z-преобразование входного сигнала как сумма расширенных версий z-преобразований многофазных компонентов.

$X (z) = \sum_{n} x (2 n) z^{- 2 n} + \sum_{n} x (2 n + 1) z^{- 2 n + 1} = X_{0} (z^{2}) + z^{- 1} X_{1} (z^{2})$

Разделите, предскажите, и обновление

Один поднимающийся шаг может быть описан следующими тремя основными операциями:

Разделите — сигнал на непересекающиеся компоненты. Распространенный способ сделать это должно извлечь четные и нечетные многофазные компоненты, объясненные в Многофазном Представлении. Это также известно как ленивый вейвлет.
Предскажите — нечетное многофазное компонентно-ориентированное на линейной комбинации выборок ровного многофазного компонента. Выборки нечетного многофазного компонента заменяются различием между нечетным многофазным компонентом и ожидаемым значением. Предсказать операция также упоминается как двойной поднимающийся шаг.
Обновление — даже многофазный компонентно-ориентированный на линейной комбинации выборок различия, полученных из предсказать шага. Шаг обновления также упоминается как основной поднимающийся шаг.

На практике нормализация включена и для основных и для двойных подъемов.

Следующая схема иллюстрирует один поднимающийся шаг.

Вейвлет Хаара через подъем

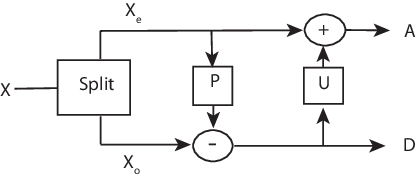
Используя операции, заданные в Разделении, Предскажите, и Обновление, можно реализовать вейвлет Хаара через подъем.

Разделите — Делят сигнал на четные и нечетные многофазные компоненты.
Предскажите — Замена x(2n+1) с d(n) =x(2n+1)–x(2n). Предсказать оператором является просто x(2n).
Обновление — Замена x(2n) с x(2n) +d(n)/2. Это равно (x(2n) +x(2n+1))/2.

Двойной подъем в z области может быть написан в следующей матричной форме

$(\begin{matrix} 10 \\ - P (z) & 1 \end{matrix}) (\begin{matrix} X_{0} (z) \\ X_{1} (z) \end{matrix})$

с P(z) =1.

Основной подъем может быть написан в z области в следующей матричной форме

$(\begin{matrix} 1 & S (z) \\ 01 \end{matrix}) (\begin{matrix} 10 \\ - P (z) & 1 \end{matrix}) (\begin{matrix} X_{0} (z) \\ X_{1} (z) \end{matrix})$

с S(z) =1/2.

Наконец, основная и двойная нормализация может быть включена можно следующим образом.

$(\begin{matrix} \sqrt{2} \\ 00 & \frac{1}{\sqrt{2}} \end{matrix}) (\begin{matrix} 1 & S (z) \\ 01 \end{matrix}) (\begin{matrix} 10 \\ - P (z) & 1 \end{matrix}) (\begin{matrix} X_{0} (z) \\ X_{1} (z) \end{matrix})$

Создать этот поднимающийся шаг в MATLAB^®, введите:

LiftHaar = liftwave('haar');
displs(LiftHaar)

Следующее отображено в окне команды MATLAB.

LiftHaar = {...                      
'd'             [ -1.00000000]  [0]  
'p'             [  0.50000000]  [0]  
[  1.41421356]  [  0.70710678]  []   
};

'd' обозначает двойной подъем. Обратите внимание на то, что для удобства, знак минус включен в двойной поднимающийся шаг в программном обеспечении Wavelet Toolbox. 'p' обозначает, что основной подъем и [ 1.41421356] [ 0.70710678] являются основными и двойными константами нормализации. LiftHaar{1,3} и LiftHaar{2,3} дают самую высокую степень полиномов Лорана, которые описывают двойные и основные подъемы. В этом случае оба - нуль, потому что двойные и основные подъемы оба описаны скалярами.

Вейвлет Bior2.2 через подъем

Этот пример представляет поднимающуюся схему bior2.2 биоортогональное масштабирование и фильтры вейвлета.

В Хааре, снимающем схему, двойной подъем (предсказывают оператор), differenced четные и нечетные выборки. В этом примере задайте новое, предсказывают оператор, который вычисляет среднее значение двух, соседних даже выборки. Вычтите среднее значение из прошедшей нечетной выборки.

$d (n) = x (2 n + 1) - \frac{}{12} [x (2 n) + x (2 n + 2)]$

В z-области можно записать двойной поднимающийся шаг как

$(\begin{matrix} 10 \\ - \frac{}{12} (1 + z) & 1 \end{matrix}) (\begin{matrix} X_{0} (z) \\ X_{1} (z) \end{matrix})$

Чтобы получить основной подъем или обновить, исследуют основной подъем в Вейвлете Хаара Через Подъем. Обновление задано таким способом, которым сумма коэффициентов приближения пропорциональна среднему значению вектора входных данных.

$\sum_{n} x (n) = \frac{}{12} \sum_{n} a (n)$

Чтобы получить тот же результат на этом поднимающемся шаге, задайте обновление как

$(\begin{matrix} 1 & \frac{}{14} (z^{- 1} + 1) \\ 01 \end{matrix}) (\begin{matrix} 10 \\ - \frac{}{12} (1 + z) & 1 \end{matrix}) (\begin{matrix} X_{0} (z) \\ X_{1} (z) \end{matrix})$

Получить эту поднимающуюся схему в командной строке, введите:

liftwave('bior2.2')

Подъем функций

Поднимающиеся функции тулбокса организованы в пять групп:

Подъем схем

FunctionName	Описание
`lsinfo`	Информация о подъеме схем
`displs`	Отобразите поднимающуюся схему
`addlift`	Добавьте основные или двойные элементарные поднимающиеся шаги в поднимающуюся схему
`wavenames`	Вейвлеты с подъемом схем

Биоортогональные квадруплетные фильтров и подъема схем

Эти схемы подъема подключения функций к биоортогональным квадруплетным фильтров и сопоставленного масштабирования и пар функции вейвлета.

FunctionName	Описание
`liftfilt`	Примените элементарные поднимающиеся шаги на квадруплет фильтров
`filt2ls`	Преобразуйте квадруплет фильтров к поднимающейся схеме
`ls2filt`	Преобразуйте поднимающуюся схему к квадруплету фильтров
`bswfun`	Вычислите и постройте биоортогональное “масштабирование и вейвлет” функции

Обычные биоортогональные квадруплетные

Эти функции предоставляют некоторым основным поднимающимся схемам, сопоставленным некоторые обычные ортогональные или биоортогональные (“истинные”) вейвлеты и “ленивый”. Эти схемы могут использоваться, чтобы инициализировать поднимающуюся процедуру.

FunctionName	Описание
`wavenames`	Обеспечивает обычные имена вейвлета, доступные для LWT
`liftwave`	Обеспечивает подъем схемы, сопоставленной с обычным вейвлетом
`wave2lp`	Предоставляет полиномам Лорана, сопоставленным обычный вейвлет

Подъем вейвлета преобразовывает (LWT)

Эти функции содержат прямые и обратные файлы подъема вейвлета преобразовывает (LWT) и для 1D и для 2D сигналов. LWT уменьшает до многофазной версии алгоритма DWT с дополняющим нуль дополнительным режимом и без дополнительных коэффициентов.

FunctionName	Описание
`lwt`	1D поднимающийся вейвлет преобразовывает
`ilwt`	Обратный 1D поднимающийся вейвлет преобразовывает
`lwtcoef`	Извлеките или восстановите 1D коэффициенты вейвлета LWT
`lwt2`	2D поднимающийся вейвлет преобразовывает
`ilwt2`	Обратный 2D поднимающийся вейвлет преобразовывает
`lwtcoef2`	Извлеките или восстановите 2D коэффициенты вейвлета LWT

Полиномы Лорана и матрицы

Эти функции разрешают запись в представление и исчисление полиномов Лорана и матриц.

FunctionName	Описание
`laurpoly`	Конструктор для класса полиномов Лорана
`laurmat`	Конструктор для класса матриц Лорана

Поднимающаяся папка и две объектных папки @laurpoly и @laurmat содержат много других файлов.

Основной подъем от Хаара

Эти два простых примера иллюстрируют основную поднимающуюся поддержку программного обеспечения Wavelet Toolbox.

Основной подъем, начинающий с вейвлета Хаара.

Запустите с вейвлета Хаара и получите соответствующую поднимающуюся схему.

lshaar = liftwave('haar');
displs(lshaar);

Добавьте основной ELS в поднимающуюся схему.

els = {'p',[-0.125 0.125],0};
lsnew = addlift(lshaar,els);
displs(lsnew);

Преобразуйте поднимающуюся схему к биоортогональному квадруплету фильтров и постройте получившуюся функцию масштабирования и вейвлет.

[LoD,HiD,LoR,HiR] = ls2filt(lsnew);
bswfun(LoD,HiD,LoR,HiR,'plot');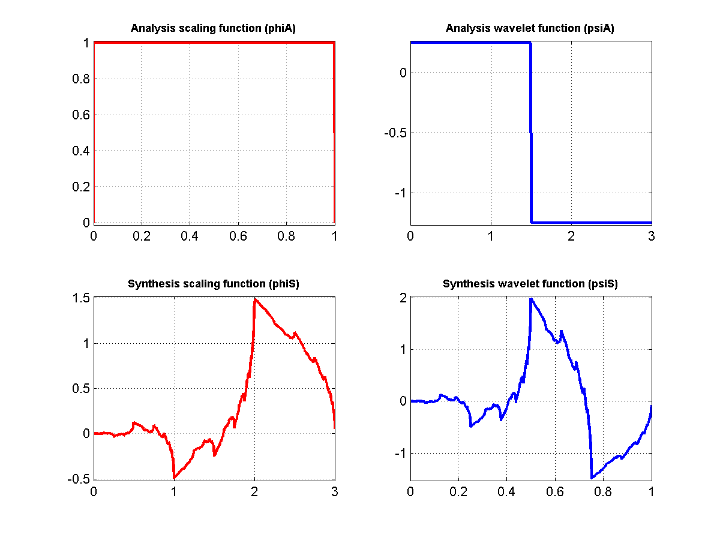

Вейвлет от целого числа к целому числу преобразовывает

В нескольких приложениях желательно иметь вейвлет, преобразовывают, который сопоставляет целочисленные входные параметры с целочисленным масштабированием и коэффициентами вейвлета. Можно выполнить легко подъем использования.

Запустите с Преобразования Хаара для целого числа к целочисленному вейвлету, преобразовывают и применяют основной поднимающийся шаг.

lshaar = liftwave('haar','int2int');
els = {'p',[-0.125 0.125],0};
lsnewint = addlift(lshaar,els);

Получите преобразование вейвлета от целого числа к целому числу 1D сигнала и инвертируйте преобразование, чтобы продемонстрировать совершенную реконструкцию.

x = 1:8;
[cA,cD] = lwt(x,lsnewint);
xnew = ilwt(cA,cD,lsnewint)

Документация