Объекты модели Econometrics Toolbox, свойства и Функции объекта

Объекты модели

После того, как у вас будет потенциальная модель для ваших данных, необходимо задать модель к MATLAB^®, чтобы возобновить анализ. Econometrics Toolbox™ имеет объекты модели для хранения эконометрических моделей дискретного времени.

Для одномерного ряда доступные объекты модели:

arima — для интегрированных, авторегрессивных моделей (ARIMA) скользящего среднего значения, опционально содержащих внешние переменные предикторы
garch — для обобщенного авторегрессивного условного выражения heteroscedasticity модели (GARCH)
egarch — для экспоненциальных моделей GARCH
gjr — для моделей Glosten-Jagannathan-Runkle
regARIMA — для моделей регрессии с ошибками ARIMA

Для многомерного ряда доступные объекты модели:

varm — для векторных моделей авторегрессии, опционально содержащих внешние переменные предикторы
vecm — для векторного исправления ошибок (cointegrated VARM) модели, опционально содержащие внешние переменные предикторы

Econometrics Toolbox поддерживает одномерный Байесов анализ линейной регрессии. Байесовы объекты модели линейной регрессии задают объединенное предшествующее распределение отклонения воздействия и коэффициентов регрессии. Доступные предшествующие объекты модели:

conjugateblm — поскольку нормальная обратная гамма спрягает предшествующую модель. Коэффициенты регрессии и отклонение воздействия являются зависимыми случайными переменными.
semiconjugateblm — поскольку нормальная обратная гамма полуспрягает предшествующую модель. Коэффициенты регрессии и отклонение воздействия являются независимыми случайными переменными.
diffuseblm — объединенное предшествующее распределение пропорционально инверсии отклонения воздействия.
empiricalblm — объединенное предшествующее распределение задано случайной выборкой от объединенного апостериорного распределения.
customblm — объединенное предшествующее распределение задано в пользовательской функции, которую вы объявляете.

Чтобы выполнить Байесов выбор переменной, доступные предшествующие объекты модели:

mixconjugateblm — для выполнения стохастического поискового выбора переменной (SSVS). Коэффициенты регрессии и отклонение воздействия являются зависимыми случайными переменными (предшествующие и апостериорные распределения сопряжены).
mixsemiconjugateblm — для выполнения SSVS. Коэффициенты регрессии и отклонение воздействия являются независимыми случайными переменными (предшествующие и апостериорные распределения полусопряжены).
lassoblm — для выполнения Байесовой регрессии лассо.

Моделирование поддержек Econometrics Toolbox и анализ дискретного или непрерывного состояния модели Маркова. Доступные объекты модели:

dtmc — для моделей дискретной цепи Маркова, охарактеризованных матрицами перехода.
ssm — для непрерывных, многомерных моделей в пространстве состояний, опционально содержащих внешние переменные предикторы
dssm — для непрерывных, многомерных моделей в пространстве состояний с рассеянными начальными состояниями, опционально содержащими внешние переменные предикторы

Чтобы создать объект модели, задайте форму своей модели к одной из функций модели (например, arima или garch). Функция создает объект модели соответствующего типа в рабочем пространстве MATLAB, как показано в фигуре.

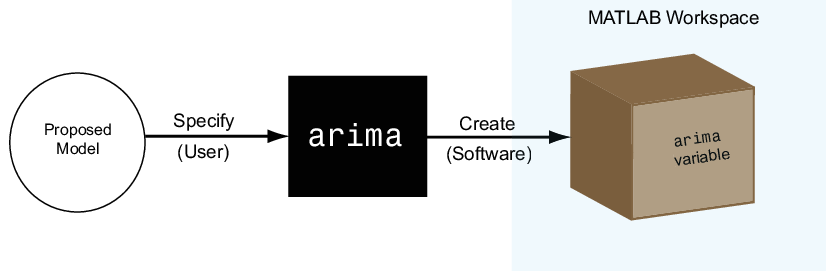
Можно работать с объектами модели, как вы были бы с любой другой переменной в MATLAB. Например, можно присвоить переменную объекта имя, просмотреть ее в рабочем пространстве MATLAB и отобразить его значение в Командном окне путем введения его имени.

Это изображение показывает рабочую область, содержащую arima модель под названием Mdl.

Свойства модели

Объект модели содержит всю информацию, необходимую для оценки, симулируйте и предскажите эконометрические модели. Эта информация включает:

Параметрическая форма модели
Количество параметров модели (например, степень модели)
Инновационное распределение (t гауссова или Студента)
Сумма преддемонстрационных данных должна была инициализировать модель

Такими данными является properties модели, которые хранятся как поля в объекте модели. Таким образом объект модели напоминает структуру данных MATLAB (struct массив.

Эти пять типов модели — arima, garch, egarch, gjr, и regARIMA— имейте свойства согласно эконометрическим моделям, которые они поддерживают. Каждое свойство имеет предопределенное имя, которое вы не можете поменять.

Например, arima условное выражение поддержек означает модели (мультипликативный и аддитивный AR, MA, ARMA, ARIMA и процессы ARIMAX). Каждый arima объект модели имеет эти свойства, показанные с их соответствующими именами.

PropertyName	Описание свойства
`Constant`	Константа модели
`AR`	Несезонные коэффициенты AR
`MA`	Несезонные коэффициенты MA
`SAR`	Сезонные коэффициенты AR (в мультипликативной модели)
`SMA`	Сезонные коэффициенты MA (в мультипликативной модели)
`D`	Степень несезонного дифференцирования
`Seasonality`	Степень сезонного дифференцирования
`Variance`	Отклонение инновационного распределения
`Distribution`	Параметрическое семейство инновационного распределения
`P`	Сумма преддемонстрационных данных должна была инициализировать компонент AR модели
`Q`	Сумма преддемонстрационных данных должна была инициализировать компонент MA модели

Когда объект модели будет существовать в рабочей области, дважды кликните ее имя в окне Workspace, чтобы открыть Редактора переменных. Редактор переменных показывает все свойства модели и их имена.

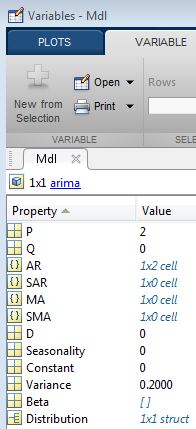
Заметьте, что в дополнение к имени, каждое свойство имеет значение.

Задайте модели

Задайте модель путем присвоения значений свойствам модели. Вам не нужно, и при этом вы не в состоянии, чтобы задать значение для каждого свойства. Функция конструктора присваивает значения по умолчанию любым свойствам, которые вы не делаете, или не может, задать.

Совет

Это - хорошая практика, чтобы знать о значениях свойств по умолчанию для любой модели, которую вы создаете.

В дополнение к наличию предопределенного имени каждое свойство модели имеет предопределенный тип данных. При присвоении или изменении значения свойства, присвоение должно быть сопоставимо с типом данных свойства.

Например, arima свойства имеют эти типы данных.

PropertyName	Тип данных свойства
`Constant`	Скаляр
`AR`	CellArray
`MA`	CellArray
`SAR`	CellArray
`SMA`	CellArray
`D`	Неотрицательное целое число
`Seasonality`	Неотрицательное целое число
`Variance`	Положительная скалярная величина
`Distribution`	`struct` массив
`P`	Неотрицательное целое число (вы не можете задать),
`Q`	Неотрицательное целое число (вы не можете задать),

Задайте AR (2) модель

Скрипт Open Live Script

Чтобы проиллюстрировать значения свойств присвоения, рассмотрите определение модели AR (2)

$y_{t} = 0.8 y_{t - 1} - 0.2 y_{t - 2} + ε_{t},$

где инновации независимы и тождественно распределили нормальные случайные переменные со средним значением 0 и отклонением 0.2. Это - условная средняя модель, так используйте arima. Присвойте значения аргументам пары "имя-значение" использования свойств модели.

Эта модель имеет два коэффициента AR, 0.8 и-0.2. Присвойте эти значения свойству AR как массив ячеек, {0.8,-0.2}. Присвойте значение 0.2 к Variance, и 0 к Constant. Вы не должны присваивать значение Distribution потому что инновационным распределением по умолчанию является 'Gaussian'. Нет никаких условий MA, сезонных условий или степеней интегрирования, не присваивайте значения этим свойствам. Вы не можете задать значения для свойств P и Q.

Таким образом, задайте модель можно следующим образом:

Mdl = arima('AR',{0.8,-0.2},'Variance',0.2,'Constant',0)

Mdl = 
  arima with properties:

     Description: "ARIMA(2,0,0) Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 2
               D: 0
               Q: 0
        Constant: 0
              AR: {0.8 -0.2} at lags [1 2]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: 0.2

Выход отображает значение созданной модели, Mdl. Заметьте что свойство Seasonality не находится в выходе. Seasonality только отображения для моделей с сезонным интегрированием. Свойство все еще присутствует, однако, как замечено в Редакторе переменных.

Mdl имеет значения для каждого arima свойство, даже при том, что спецификация, включенная только три. arima значения по умолчанию присвоений для незаданных свойств. Значения SAR, MA, и SMA массивы пустой ячейки, потому что модель не имеет никаких сезонных условий или условий MA. Значения D и Seasonality 0 потому что нет никакого несезонного или сезонного дифференцирования. arima наборы:

P равняйтесь 2, количество преддемонстрационных наблюдений должно было инициализировать модель AR (2).
Q равняйтесь 0 потому что нет никакого компонента MA к модели (т.е. никакие преддемонстрационные инновации не необходимы).

Задайте GARCH (1,1) модель

Скрипт Open Live Script

Как другой рисунок, рассмотрите определение модели GARCH(1,1)

$y_{t} = ε_{t},$

где

$\begin{array}{rcl} ε_{t} & = & σ_{t} z_{t} \\ σ_{t}^{2} & = & κ + γ_{1} σ_{t - 1}^{2} + α_{1} ε_{t - 1}^{2} \end{array}$

Принять $z_{t}$ следует за стандартным нормальным распределением.

Эта модель имеет один коэффициент GARCH (соответствующий изолированному термину отклонения) и один коэффициент ДУГИ (соответствующий изолированному инновационному термину в квадрате), оба с неизвестными значениями. Задавать эту модель, введите:

Mdl = garch('GARCH',NaN,'ARCH',NaN)

Mdl = 
  garch with properties:

     Description: "GARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
          Offset: 0

Значением по умолчанию для постоянного термина является также NaN. Параметры с NaN значения должны быть оценены или в противном случае заданы, прежде чем можно будет предсказать или симулировать модель. Существует также краткий синтаксис, чтобы создать модель GARCH(1,1) по умолчанию:

Mdl = garch(1,1)

Mdl = 
  garch with properties:

     Description: "GARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
          Offset: 0

Краткий синтаксис возвращает модель GARCH с одним коэффициентом GARCH и одним коэффициентом ДУГИ с NaN по умолчанию значения.

Получите свойства модели

Скрипт Open Live Script

Значения свойств в существующей модели восстановимы. Работа с моделями напоминает работу с struct массивы, потому что можно получить доступ к свойствам модели с помощью записи через точку. Таким образом, введите имя модели, затем имя свойства, разделенное '.' (период).

Например, рассмотрите arima модель с этим AR (2) спецификация:

Mdl = arima('AR',{0.8,-0.2},'Variance',0.2,'Constant',0);

Отобразить значение свойства AR для созданной модели, введите:

arCoefficients = Mdl.AR

arCoefficients=1×2 cell
    {[0.8000]}    {[-0.2000]}

AR массив ячеек, таким образом, необходимо использовать синтаксис массива ячеек. Содействующие массивы ячеек индексируются задержкой, таким образом входя

secondARCoefficient = Mdl.AR{2}

secondARCoefficient = -0.2000

возвращает коэффициент в задержке 2. Можно также присвоить любое значение свойства новой переменной:

ar = Mdl.AR

ar=1×2 cell
    {[0.8000]}    {[-0.2000]}

Измените свойства модели

Скрипт Open Live Script

Можно также изменить свойства модели с помощью записи через точку. Например, рассмотрите этот AR (2) спецификация:

Mdl = arima('AR',{0.8,-0.2},'Variance',0.2,'Constant',0)

Mdl = 
  arima with properties:

     Description: "ARIMA(2,0,0) Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 2
               D: 0
               Q: 0
        Constant: 0
              AR: {0.8 -0.2} at lags [1 2]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: 0.2

Созданная модель имеет Гауссово инновационное распределение по умолчанию. Измените инновационное распределение в t распределение Студента с восемью степенями свободы. Тип данных для Distribution struct массив.

Mdl.Distribution = struct('Name','t','DoF',8)

Mdl = 
  arima with properties:

     Description: "ARIMA(2,0,0) Model (t Distribution)"
    Distribution: Name = "t", DoF = 8
               P: 2
               D: 0
               Q: 0
        Constant: 0
              AR: {0.8 -0.2} at lags [1 2]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: 0.2

Переменная Mdl обновляется соответственно.

Функции объекта

Объектные функции являются функциями, которые принимают объекты модели как входные параметры. В Econometrics Toolbox эти функции, которые представляют шаги в аналитическом рабочем процессе эконометрики, принимают любой из объектов модели, включенных в тулбокс:

estimate
forecast
simulate

У модели, которую можно подбирать к данным, есть эти три общие метода, но объекты модели в тулбоксе могут иметь другие объектные функции.

Объектные функции могут различать объекты модели (например, arima модель по сравнению с garch модель). Таким образом, некоторые объектные функции принимают различные дополнительные входные параметры и возвращают различные выходные параметры в зависимости от типа модели, которая вводится.

Найдите объектные страницы ссылки на функцию для определенной модели путем ввода, например, doc arima/estimate.

Смотрите также

Объекты

arima | conjugateblm | customblm | diffuseblm | dssm | dtmc | egarch | garch | gjr | lassoblm | mixconjugateblm | mixsemiconjugateblm | regARIMA | semiconjugateblm | ssm | varm | vecm

Документация