Примеры, которые следуют, показывают, как расположить и ориентировать зубчатые тела так, чтобы они удовлетворили требованиям блока различных ограничительных блоков механизма. Каждый пример запускается с обзора соответствующих размерностей механизма и размещений системы координат. Это руководство атрибутов выбор твердых преобразований должен был гарантировать, что механизмы собираются в mesh.
Модели совместно используют ту же топологию блок-схемы, с компонентами модели — телами, соединениями, и ограничением механизма — расположенный в кинематической замкнутой цепи в каждом случае. Рисунок показывает простой цикл. Тело поставщика услуг находится в примерах, считавшихся зафиксированными к мировой системе координат с ее инерцией, следовательно, уменьшаемой до лишней детали и тела, в целом проигнорированного.
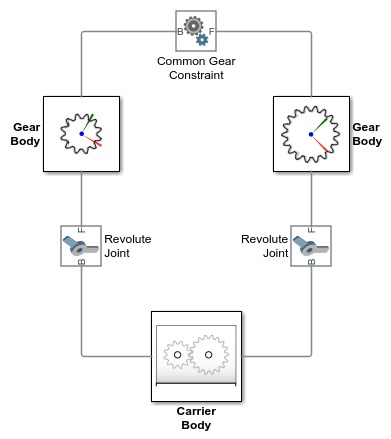
Модели включают четыре типа блоков Simscape™ Multibody™:
File Solid — Обеспечивает конфигурации механизма, инерцию и цвета. Конфигурации механизма, вместе с зубами или потоками, чтобы больше ясно показать механизмы в mesh, импортируются из файлов ШАГА. Положения систем координат механизма относительно конфигураций механизма получены из тех же файлов.
Соединение — Предоставляет зубчатым телам необходимые степени свободы. блоки Revolute Joint включают вращение вокруг одной оси. блоки Prismatic Joint включают перевод вдоль одной оси. Скоростные цели состояния, заданные в блоках соединений, приводят механизмы в движение.
Rigid Transform — Вращает и переводит соединения и присоединенные зубчатые тела так, чтобы они были правильно размещены для того, чтобы сцепиться. блоки Rigid Transform обеспечивают средние значения, чтобы изменить размещения механизма и поэтому удовлетворить требованиям блока механизма.
Ограничение механизма — Пары движения зубчатых тел. Ограничительные блоки механизма устраняют одну степень свободы между механизмами, заставляя их переместиться как будто в mesh. Витрина в качестве примера, один за другим, различные ограничительные блоки механизма.

smdoc_bevel_gear_start модель, показанная на рисунке, обеспечивает пример конического блока механизма. Модель, на основе блока Bevel Gear Constraint, завершена в каждом смысле, но один — все твердые преобразования являются нулем, и системы координат механизма являются поэтому совпадающими в пространстве.
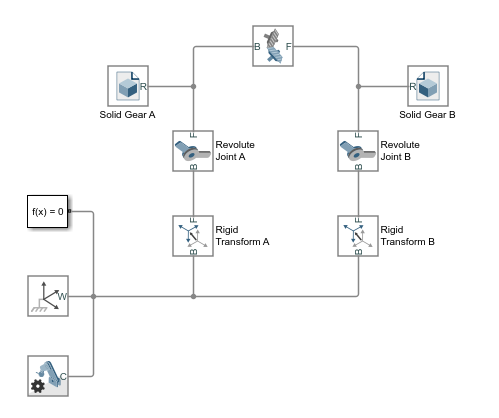
Этот короткий пример показывает, как подходящие преобразования следуют с готовностью от размерностей механизма и ограничений блока — и как, когда-то заданный в блоках Rigid Transform, они позволяют модели механизма собраться как будто в mesh без ошибки.
Конические механизмы, A и B, идентичны в размере с радиусом подачи 2.8 cm в каждом случае. Системы координат механизма помещаются с источниками в центры механизма и z - оси, выровненные с осями вращения механизма, чтобы отворачиваться от валов механизма. Это выравнивание сопоставимо с блоками Revolute Joint, которые позволяют вращение вокруг z - ось только.
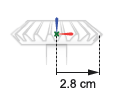
Оси вращения механизма встречаются под прямым углом. Система координат конического механизма A находится при смещении [2.8, 0, 0] cm, в Декартовых координатах, относительно мировой системы координат. Система координат конического механизма B находится при смещении [0, 0, 2.8] cm относительно мировой системы координат и под углом 90 deg о y - ось также мировой системы координат.
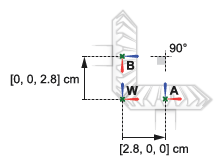
Завершите коническую модель механизма путем определения твердых преобразований, описанных в схематичном блоке механизма. Концептуальная анимация, которая следует, показывает инкрементные эффекты, что твердые преобразования имели бы, были они, чтобы применяться в последовательности во время обновления модели.
Если вы еще не сделали так, откройте неполную коническую модель механизма путем ввода имени модели, smdoc_bevel_gear_start в командной строке MATLAB®.
В диалоговом окне блока Rigid Transform A задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение конического механизма относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Cartesian |
| Offset | [2.8, 0, 0] cm |
В диалоговом окне блока Rigid Transform B задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение конического механизма B относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Cartesian |
| Offset | [0, 0, 2.8] cm |
В диалоговом окне блока Rigid Transform B задайте параметры Rotation, показанные в таблице. Эти параметры устанавливают ориентацию конического механизма B относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Standard Axis |
| Axis | +Y |
| Angle | 90 deg |
Симулируйте модель. Mechanics Explorer открывается динамической визуализацией механизма, показанной в начале этого примера.
Чтобы видеть полную коническую модель механизма, в командной строке MATLAB вводят smdoc_bevel_gear. Simscape Multibody открывает коническую модель механизма с твердыми преобразованиями, описанными в этом примере.

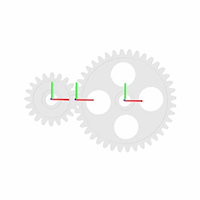
smdoc_common_gear_external_start модель, показанная на рисунке, обеспечивает пример внешнего цилиндрического блока механизма. Модель, на основе блока Common Gear Constraint, завершена в каждом смысле, но один — все твердые преобразования являются нулем, и системы координат механизма являются поэтому совпадающими в пространстве.
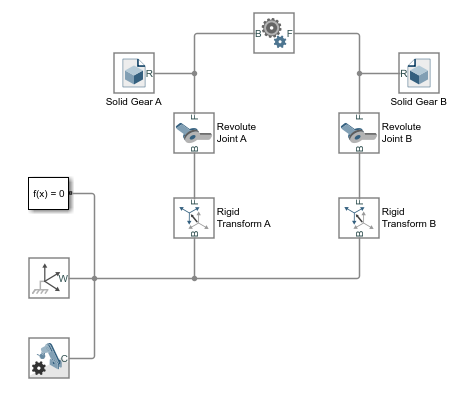
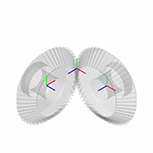
Этот короткий пример показывает, как подходящие преобразования следуют с готовностью от размерностей механизма и ограничений блока — и как, когда-то заданный в блоках Rigid Transform, они позволяют модели механизма собраться как будто в mesh без ошибки.
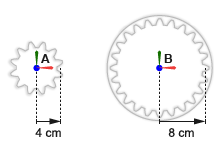
Маленький цилиндрический механизм, A, имеет радиус подачи 4 cm. Большой цилиндрический механизм, B, имеет радиус подачи 8 cm. Системы координат механизма помещаются с источниками в центры механизма и z - оси, выровненные с осями вращения механизма, чтобы отворачиваться от валов механизма. Это выравнивание сопоставимо с блоком Revolute Joint, который позволяет вращение вокруг z - ось только.
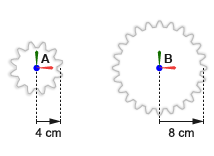
Цилиндрические оси вращения механизма параллельны друг другу. Система координат маленького цилиндрического механизма находится при смещении [-4, 0, 0] cm, в Декартовых координатах, относительно мировой системы координат. Система координат большого цилиндрического механизма находится при смещении [-8, 0, 0] cm, также относительно мировой системы координат.
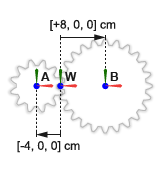
Завершите внешнюю цилиндрическую модель механизма путем определения твердых преобразований, описанных в схематичном блоке механизма. Концептуальная анимация, которая следует, показывает инкрементные эффекты, что твердые преобразования имели бы, были они, чтобы применяться в последовательности во время обновления модели.
Если вы еще не сделали так, откройте неполную коническую модель механизма путем ввода имени модели, smdoc_common_gear_external_start в командной строке MATLAB.
В диалоговом окне блока Rigid Transform A задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение маленького цилиндрического механизма, A, относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Cartesian |
| Offset | [-4, 0, 0] cm |
В диалоговом окне блока Rigid Transform B задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение большого цилиндрического механизма, B, относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Cartesian |
| Offset | [8, 0, 0] cm |
Симулируйте модель. Mechanics Explorer открывается динамической визуализацией механизма, показанной в начале этого примера.
Чтобы видеть полную внешнюю цилиндрическую модель механизма, в командной строке MATLAB вводят smdoc_common_gear_external.

smdoc_common_gear_internal_start модель, показанная на рисунке, обеспечивает пример внутреннего цилиндрического блока механизма. Модель, на основе блока Common Gear Constraint, завершена в каждом смысле, но один — все твердые преобразования являются нулем, и системы координат механизма являются поэтому совпадающими в пространстве.

Этот короткий пример показывает, как подходящие преобразования следуют с готовностью от размерностей механизма и ограничений блока — и как, когда-то заданный в блоках Rigid Transform, они позволяют модели механизма собраться как будто в mesh без ошибки.
Цилиндрический механизм, A, имеет радиус подачи 4 cm. Кольцевой механизм, B, имеет радиус подачи 8 cm. Системы координат механизма помещаются с источниками в центры механизма и z - оси, выровненные с осями вращения механизма, чтобы отворачиваться от валов механизма. Это выравнивание сопоставимо с блоком Revolute Joint, который позволяет вращение вокруг z - ось только.
Оси вращения механизма параллельны друг другу. Цилиндрическая система координат механизма находится при смещении [-4, 0, 0] cm, в Декартовом обозначении, относительно мировой системы координат. Кольцевая система координат механизма находится оставленная с ее источником и z - ось, совпадающая с теми из мировой системы координат.
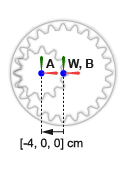
Завершите внутреннюю цилиндрическую модель механизма путем определения твердых преобразований, описанных в схематичном блоке механизма. Концептуальная анимация, которая следует, показывает инкрементные эффекты, что твердые преобразования имели бы, были они, чтобы применяться в последовательности во время обновления модели.
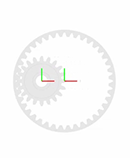
Если вы еще не сделали так, откройте неполную коническую модель механизма путем ввода имени модели, smdoc_common_gear_internal_start в командной строке MATLAB.
В диалоговом окне блока Rigid Transform A задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение цилиндрического механизма, A, относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Cartesian |
| Offset | [-4, 0, 0] cm |
Симулируйте модель. Mechanics Explorer открывается динамической визуализацией механизма, показанной в начале этого примера.
Чтобы видеть полную внутреннюю цилиндрическую модель механизма, в командной строке MATLAB вводят smdoc_common_gear_internal.
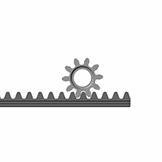
smdoc_rack_and_pinion_start модель, показанная на рисунке, обеспечивает пример блока реечного механизма. Модель, на основе блока Rack and Pinion Constraint, завершена в каждом смысле, но один — все твердые преобразования являются нулем, и системы координат механизма являются поэтому совпадающими в пространстве.
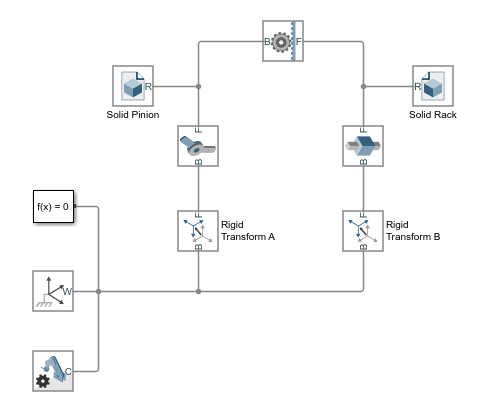
Этот короткий пример показывает, как подходящие преобразования следуют с готовностью от размерностей механизма и ограничений блока — и как, когда-то заданный в блоках Rigid Transform, они позволяют модели механизма собраться как будто в mesh без ошибки.
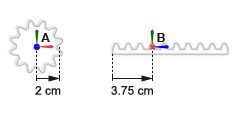
Шестерня, A, имеет радиус подачи 2 cm. Система координат шестерни помещается с источником в центр шестерни и z - ось вдоль оси шестерни. Система координат стойки помещается с источником 3.75 cm от ребра стойки и z - ось вдоль длины стойки. Выравнивания системы координат сопоставимы с Revolute Joint и блоками Prismatic Joint, которые позволяют движение об или вдоль z - ось только.
Ось перевода стойки под прямым углом к оси вращения шестерни. Система координат шестерни находится при смещении [0, 2, 0] cm, в Декартовом обозначении, относительно мировой системы координат. Система координат стойки находится под углом 90 deg относительно положительного y - ось мировой системы координат.
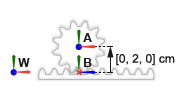
Завершите модель реечного механизма путем определения твердых преобразований, описанных в схематичном блоке механизма. Концептуальная анимация, которая следует, показывает инкрементные эффекты, что твердые преобразования имели бы, были они, чтобы применяться в последовательности во время обновления модели.
Если вы еще не сделали так, откройте неполную коническую модель механизма путем ввода имени модели, smdoc_rack_and_pinion_start в командной строке MATLAB.
В диалоговом окне блока Rigid Transform A задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение шестерни, A, относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Cartesian |
| Offset | [0, 2, 0] cm |
В диалоговом окне блока Rigid Transform B задайте параметры Rotation, показанные в таблице. Эти параметры устанавливают ориентацию стойки, B, относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Standard Axis |
| Axis | +Y |
| Angle | 90 deg |
Симулируйте модель. Mechanics Explorer открывается динамической визуализацией механизма, показанной в начале этого примера.
Чтобы видеть полную модель реечного механизма, в командной строке MATLAB вводят smdoc_rack_and_pinion.

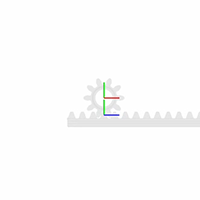
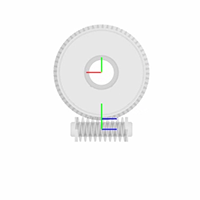
smdoc_worm_and_gear_start модель, показанная на рисунке, обеспечивает пример блока червя-и-механизма. Модель, на основе блока Worm and Gear Constraint, завершена в каждом смысле, но один — все твердые преобразования являются нулем, и системы координат механизма являются поэтому совпадающими в пространстве.
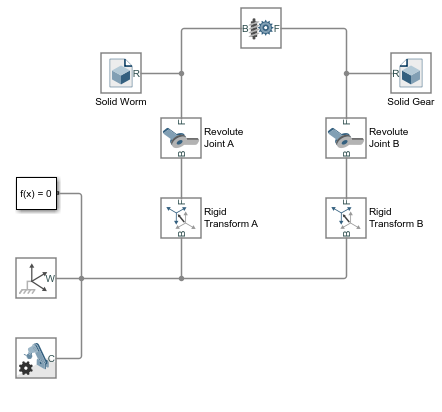
Этот короткий пример показывает, как подходящие преобразования следуют с готовностью от размерностей механизма и ограничений блока — и как, когда-то заданный в блоках Rigid Transform, они позволяют модели механизма собраться как будто в mesh без ошибки.
У червя, A, есть радиус подачи 0.85 cm. Механизм, B, имеет радиус подачи 3.75 cm. Червь и системы координат механизма размещаются с источниками в центры геометрии и z - оси, выровненные с соответствующими осями вращения. Это выравнивание сопоставимо с блоком Revolute Joint, который позволяет вращение вокруг z - ось только.
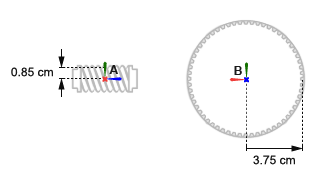
Ось вращения червя под прямым углом к оси вращения механизма. Система координат червя находится при смещении [0, -0.85, 0] cm, в Декартовом обозначении, относительно мировой системы координат. Система координат механизма находится при смещении [0, +3.75, 0] cm и под углом 90 deg о положительном y - ось относительно мировой системы координат.
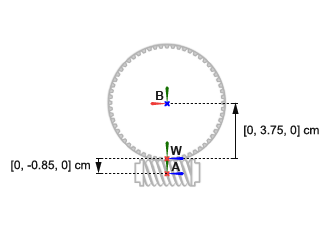
Завершите модель червя-и-механизма путем определения твердых преобразований, описанных в схематичном блоке механизма. Концептуальная анимация, которая следует, показывает инкрементные эффекты, что твердые преобразования имели бы, были они, чтобы применяться в последовательности во время обновления модели.
Если вы еще не сделали так, откройте неполную коническую модель механизма путем ввода имени модели, smdoc_worm_and_gear_start в командной строке MATLAB.
В диалоговом окне блока Rigid Transform A задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение червя, A, относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Cartesian |
| Offset | [0, -0.85, 0] cm |
В диалоговом окне блока Rigid Transform A задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение механизма, B, относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Cartesian |
| Offset | [0, 3.75, 0] cm |
В диалоговом окне блока Rigid Transform B задайте параметры Rotation, показанные в таблице. Эти параметры устанавливают ориентацию механизма, B, относительно мировой системы координат как описано в схематичном блоке Механизма.
| Параметр | Установка |
|---|---|
| Method | Standard Axis |
| Axis | +Y |
| Angle | 90 deg |
Симулируйте модель. Mechanics Explorer открывается динамической визуализацией механизма, показанной в начале этого примера.
Чтобы видеть полную модель механизма червя-и-механизма, в командной строке MATLAB вводят smdoc_worm_and_gear.