Анализ устойчивости Используя дисковые поля

Дисковые поля определяют количество устойчивости системы с обратной связью против изменений усиления цикла или фазы на любой частоте. diskmargin команда моделирует такие изменения как мультипликативная неопределенность объекта на передаточной функции разомкнутого цикла L. disk margin измеряется, сколько неопределенности цикл может терпеть прежде, чем идти нестабильный. От той суммы неопределенности, diskmargin выводит минимальные запасы по амплитуде и фазе. Находящийся на диске GM запаса по амплитуде является суммой, которой усиление цикла может увеличиться или уменьшиться без потери устойчивости в абсолютных единицах. Находящийся на диске PM запаса по фазе является суммой, которой фаза цикла может увеличиться или уменьшиться без потери устойчивости в градусах. Эти находящиеся на диске поля учитывают всю частоту и взаимодействия цикла. Поэтому находящийся на диске граничный анализ обеспечивает более сильную гарантию устойчивости, чем классические запасы по амплитуде и фазе, вычисленные с allmargin.

Цикл за один раз и многоконтурные поля

Для обратной связи MIMO можно вычислить:

Поля Loop-at-a-time — Максимальные терпимые изменения усиления (или изменения фазы) в каждом канале обратной связи, вычисленном со всеми другими замкнутыми кругами.
Multiloop margins — Максимальные терпимые изменения усиления (или изменения фазы) через все каналы обратной связи. Многоконтурные поля допускают независимые и параллельные изменения всех каналов обратной связи. Многоконтурные поля получают взаимодействия цикла и обычно дают к меньшим полям.

Например, рассмотрите систему MIMO с 2 каналами следующего рисунка.

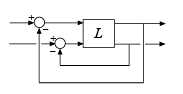
Для этой системы можно вычислить:

Максимальные терпимые изменения усиления (или изменения фазы) в первом канале (первый системный вход к первой системе выход)
Максимальные терпимые изменения усиления (или изменения фазы) во втором канале (второй системный вход к второй системе выход)
Максимальные терпимые независимые изменения усиления (или изменения фазы) в обоих каналах одновременно.

В общем случае запасы по амплитуде и фазе варьируются через частоту. Таким образом, например, Например, запас по амплитуде 5 дБ на уровне 2 рад/с в конкретном канале цикла указывает, что устойчивость с обратной связью обеспечена когда увеличения усиления цикла или уменьшения на целых 5 дБ на той частоте.

Для получения дополнительной информации и примеры того, как получить находящиеся на диске запасы устойчивости, смотрите diskmargin.

Изменения во входе объекта или объекте Выход

В некоторых случаях запасы устойчивости могут варьироваться в зависимости от того, применяются ли усиление и изменения фазы во входе объекта или объекте выход. diskmargin позволяет вам вычислить поля для изменений во входе, вывести, или оба одновременно. В общем случае поля для одновременных изменений ввода и вывода меньше, чем те для ввода или вывода только и обеспечивают более консервативную гарантию устойчивости. Считайте SISO или MIMO системой с обратной связью следующей схемы.

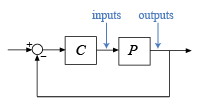
Можно вычислить дисковые поля при вводах и выводах объекта можно следующим образом.

[DM,MM] = diskmargin(P*C) возвращает поля для изменений на объекте выходные параметры.
[DM,MM] = diskmargin(C*P) возвращает поля для изменений во входных параметрах объекта.
MMIO = diskmargin(P,C) возвращает поля для одновременных изменений на объекте выходные параметры и входные параметры.

Для получения дополнительной информации и примеры того, как получить эти поля, смотрите diskmargin.

Объединенные изменения усиления и фазы

Запасы по амплитуде вы получаете из diskmargin не примите изменение фазы, и наоборот. На практике ваша система может испытать одновременное усиление и изменения фазы. Следующий график может помочь вам оценить робастность к изменениям и в усилении и в фазе.

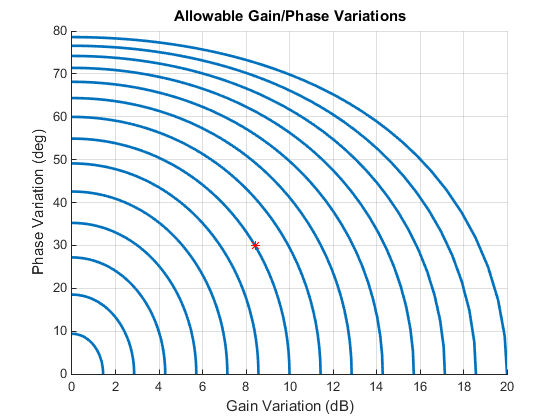
Например, предположите, что обратная связь в вашей системе имеет поле на 10 дБ на особой частоте. Контур, запускающийся в (Gain,Phase) = (10,0) показывает, как данный объем изменения фазы уменьшает допустимое изменение усиления на той частоте. Например, если фаза варьируется 30 градусами, то спады запаса по амплитуде приблизительно до 8,4 дБ (красная метка).

Дисковые поля худшего случая

Дисковое поле вычисляется путем применения неопределенности к номинальной передаче цикла L и вычисление, как большой, что неопределенность может быть при сохранении устойчивости с обратной связью (см., Как Дисковые Поля Вычисляются). Если передача цикла, L является самостоятельно неопределенной системой, то дисковое поле также варьируется как функция системной неопределенности. worst-case disk margin является самым маленьким дисковым полем, которое происходит в указанном диапазоне неопределенности. Это - также минимальное гарантируемое поле в области значений неопределенности. Можно вычислить дисковые поля худшего случая неопределенной системы с помощью wcdiskmargin. Эта функция оценивает дисковые поля худшего случая и соответствующие запасы по амплитуде и фазе худшего случая и для цикла за один раз и для многоконтурных изменений. Функция также возвращает возмущение худшего случая, комбинацию неопределенных элементов в L, который дает к самым слабым полям.

Как Вычисляются Дисковые Поля

Полагайте, что следующая система с обратной связью, с номинальным циклом передают модульная обратная связь и L.

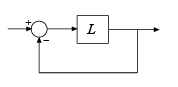
Для SISO L граничный диском анализ включает мультипликативную комплексную неопределенность Δ в передаточную функцию цикла можно следующим образом:

$L \to L_{Δ} = L \frac{1 + Δ (1 - E) / 2}{1 - Δ (1 + E) / 2} = L (1 + δ_{L}), | Δ | < α .$

Для Δ = 0, мультипликативный фактор равняется 1, соответствуя номинальному L. Когда Δ варьируется по шару | Δ | <α, фактор (1 + _δL) варьируется по диску. Усиление и фаза фактора являются моделью для усиления и изменения фазы L. Параметр эксцентриситета E варьируется форма диска. disk margin является наименьшим значением α, в котором система с обратной связью становится нестабильной (см. [1]).

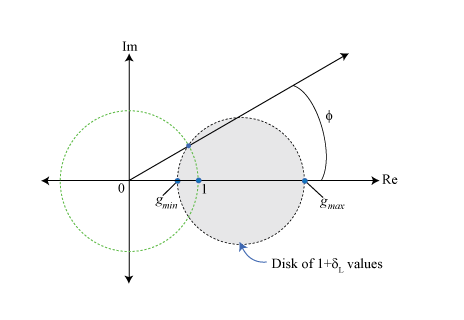
От этого значения α, diskmargin вычисляет минимальные гарантируемые запасы по амплитуде и фазе. Теневая область на следующем рисунке показывает область значений (1 + _δL) значения в комплексной плоскости для | Δ | <α и зафиксировала E. Запасы по амплитуде [_gmin, _gmax] является точками, где диск прерывает вещественную ось. Усиление может варьироваться любым, включают эту область значений, не ставя под угрозу устойчивость. Запас по фазе является углом ϕ между вещественной осью и пересечением диска и модульного круга, сосредоточенного на источнике. Система может терпеть изменения в фазе ±ϕ.

С этой неопределенностью, к которой применяются L, система с обратной связью остается устойчивой для всех | Δ | <α когда для всех частот ω,

$| S (j ω) + \frac{E - 1}{2} I | < \frac{1}{α},$

где S является функцией чувствительности (I + L) ^–1. Другими словами, α может быть вычислен из пикового усиления переключенной функции чувствительности,

$S + \frac{(E - 1) I}{2} .$

В плоскости Найквиста требовании устойчивой устойчивости для | Δ | <α эквивалентен:

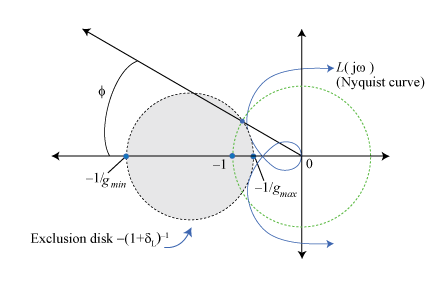
$L (j ω) \neq - \frac{1 - Δ (1 + E) / 2}{1 + Δ (1 - E) / 2}, for \forall ω and для всего | Δ | < α .$

Левая сторона этого выражения является кривой Найквиста передачи цикла. Правая сторона – (1 + _δL) ^–1 , отрицательная инверсия фактора неопределенности применилась к L. Для фиксированного E это - диск, размер которого растет с α. Дисковое поле соответствует самому большому α, для которого этот диск не пересекает кривую Найквиста. Таким образом устойчивость системы с обратной связью гарантируется, если кривая не пересечет этот диск исключения, как проиллюстрировано в следующей схеме.

Эффект дисковой формы на дисковых полях

Скрипт Open Live Script

Варьируясь параметр эксцентриситета E составляет изменение формы диска неопределенности $(1 + δ)$ из которого выведены запасы по амплитуде и фазе. Диски различных форм дают более или менее скромные подсчеты полей. Таким образом можно исследовать поля, следующие из различных значений E, чтобы получить наименее осторожную оценку для системы.

Чтобы видеть, как дисковое изменение полей параметром эксцентриситета для конкретной передаточной функции разомкнутого цикла L, варьируйтесь E между большими отрицательными и большими положительными значениями. Постройте получившиеся запасы по амплитуде и фазе.

L = tf(25,[1 10 10 10]);
% Generate vector of E values
E = [linspace(0,1,10) logspace(0,2,10)];
E = unique([E -E]);
% Compute disk margins
for ct=1:numel(E)
    DM(ct) = diskmargin(ss(L),E(ct));
end
% Extract and plot gain and phase margin values against E
GM = cat(1,DM.GainMargin);
PM = cat(1,DM.PhaseMargin);

subplot(211) 
plot(E,GM(:,1),E,GM(:,2))
title('GM'), grid

subplot(212)
plot(E,PM(:,1),E,PM(:,2))
title('PM'), grid

Рассмотрите график запаса по амплитуде. Для этой системы большие отрицательные величины E дают очень осторожную оценку для верхнего поля, но намного менее осторожную оценку нижнего поля. Реверс верен для больших положительных значений E. Истинные поля системы должны охватить все эти оценки. Поэтому можно прийти к заключению, что цикл остается устойчивым для изменений усиления цикла в полном спектре между самым низким нижним полем и самым высоким верхним полем или факторами приблизительно 0.08-1.9.

Для запасов по фазе наименее осторожная оценка приблизительно ±25 ° происходит ближе с E = 0.

Чтобы видеть, как изменение значений E соответствует различным дисковым формам, исследуйте годограф Найквиста системы и дисков, соответствующих нескольким значений E. Можно найти диск для особого значения E путем установки $Δ = α e^{i θ}$ и варьирование $θ$ между 0 и $π$ . Дисковое поле $α$ возвращен diskmargin в DiskMargin поле DM.

figure
nyquist(L,'b')
hold on

Evalues = [-3,0,3];
disk = [];

for k = 1:length(Evalues)
    E = Evalues(k);
    DM = diskmargin(L,E);
    theta = 0:0.01:2*pi;
    delta = DM.DiskMargin * exp(1i*theta);
    ExcludeRegion = (delta*(1+E)/2-1) ./ (1+delta*(1-E)/2);
    disk(:,k) = ExcludeRegion';
end

plot(disk)
axis equal
legend('L','E = -3','E = 0','E = 3')

Для видимости график показывает только три значения E, –3, 0, и 3. График показывает, как форма диска, и таким образом получившиеся дисковые поля, варьируются как E изменения.

Модель неопределенности MIMO

Для систем MIMO дисковый расчет поля аналогичен. Модель неопределенности:

$L \to L_{Δ} = L (I + Δ \frac{1 - E}{2}) {(I - Δ \frac{1 + E}{2})}^{- 1} .$

Здесь, Δ является диагональной матрицей, чтобы смоделировать усиление или изменение фазы независимо каждого канала обратной связи.

$Δ = (\begin{matrix} δ_{1} \\ 000 & ⋱ \\ 000 & δ_{N} \end{matrix}), | δ_{j} | < α .$

Устойчивое условие устойчивости затем:

$μ_{Δ} (S + \frac{E - 1}{2} I) < \frac{1}{α} .$

Дисковое поле α может быть получен μ, структурировало сингулярное значение (mussv) расчет.

Дисковые поля и настройка системы управления

Настраивающие инструменты системы управления в Control System Toolbox™ позволяют вам задать целевые циклы for запасов по амплитуде и фазе в своей настроенной системе. Граничные цели TuningGoal.Margins (для настройки командной строки), и Цель Полей (для настройки с Control System Tuner) используют находящиеся на диске поля. Таким образом, когда вы задаете независимые запасы по амплитуде и фазе GM и PM для настройки, программное обеспечение выбирает самый маленький α, который осуществляет оба значения. Этим α дают:

$α = \max [\frac{G M - 1}{G M + 1}, \tan (P M / 2)] .$

В применении этого значения α настраивающееся программное обеспечение принимает E = 0.

Ссылки

[1] Загубите, степень доктора юридических наук, Р.Л. Дэйли, и Д. Гэнгсаас. "Практический Проект Закона о надзоре для Самолета Используя Многомерные Методы". Международный журнал Управления. Издание 59, Номер 1, 1994, стр 93–137.

Смотрите также

diskmargin | wcdiskmargin

Документация