airyBi
Функция Эйри второго вида
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
airyBi(z) airyBi(z,n)
Описание
airyBi(z) представляет функцию Эйри второго вида. Функции Эйри первого и второго вида являются линейно независимыми решениями дифференциального уравнения
.
airyBi(z, n) представляет n- производная th airyBi(z) относительно z.
airyBi(z) эквивалентно airyBi(z, 0).
Для n ≥ 2, производные функций Эйри автоматически выражаются в терминах функций Эйри и их первой производной. Смотрите Пример 1.
airyBi возвращает специальные значения для z = 0 и z = ±∞. Для всех других символьных значений z возвращены неоцененные вызовы функции. Смотрите Пример 2.
Взаимодействия среды
Когда названо аргументами с плавающей точкой, это функционирует, чувствительно к переменной окружения DIGITS который определяет числовую рабочую точность.
Примеры
Пример 1
Вторые и производные высшего порядка функций Эйри переписаны в терминах функций Эйри и их первых производных:
airyBi(x), airyBi(x, 1), airyBi(sin(x), 3)
Пример 2
Для z = 0, возвращены специальные значения:
airyBi(0), airyBi(0, 1), airyBi(0, 27)
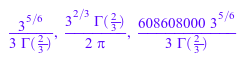
Для n = 0, n = 1 и любой символьный z ≠ 0, z ≠ ±∞, отвечают на символьный звонок:
airyBi(-1), airyBi(x, 1)
Значения с плавающей точкой возвращены для аргументов с плавающей точкой:
airyBi(0.0), airyBi(-3.24819, 1), airyBi(-3.45 + 2.75*I)
Пример 3
diff, float, limit, series, и другие функции обрабатывают выражения, включающие функции Эйри:
diff(airyBi(x^2), x)
float(airyBi(PI))
limit(airyBi(-x), x = infinity)
series(airyBi(x, 1), x = infinity)
Параметры
| |
|
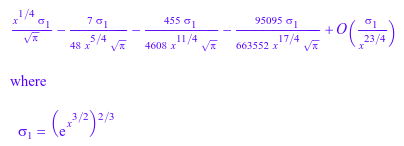
Арифметическое выражение, представляющее неотрицательное целое число |
Возвращаемые значения
Арифметическое выражение.
Перегруженный
z