DiscontinuitySearchПолусимвольный поиск разрывов
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
| Объекты | Значения по умолчанию DiscontinuitySearch |
|---|---|
plot::Curve2d, plot::Curve3d, plot::Function2d, plot::Polar, plot::Sweep | TRUE |
DiscontinuitySearch = TRUE по сравнению с DiscontinuitySearch = FALSE определяет, проверяется ли графический объект (полу-) символически для разрывов и сингулярности.
Определенные графические объекты, такие как функциональные графики или параметризованные кривые могут иметь сингулярность. Это может создать графические артефакты, такие как побочные линии между числовыми точками выборки, которые заключают сингулярность. С DiscontinuitySearch = TRUE, объект предварительно обрабатывается, чтобы найти потенциальную сингулярность. Если особые точки найдены, объект разделен в несколько непересекающихся подобъектов (“ветви”), каждая из которых является гладкой.
DiscontinuitySearch только доступно для объектов линии (2D функциональные графики и параметризованные кривые в 2D и 3D). Это не доступно для объектов подложки, таких как 3D функциональные графики и параметризованные поверхности!
Разрывы будут только обнаружены, если они будут вызваны системными функциями, которые реализованы как функциональная среда с соответствующим "realDiscont" или "numericDiscont" паз.
Поиск разрывов использует арифметику интервала. Если специальные функции будут включены, которые не поддерживают этот вид арифметики, поиск не успешно выполнится.
По причинам КПД рекомендуется отключить поиск разрывов с DiscontinuitySearch = FALSE когда известно, что графический объект непрерывен.
Следующий график содержит полюса первого порядка. Когда поиск разрыва отключен, побочные вертикальные линии происходят, соединяя точки выборки слева от полюса с соседними точками выборки справа от полюса. Далее, окружение полюсов плохо производится:
plot(plot::Function2d(tan(x^2), x=-3..3,
ViewingBoxYRange = -10..10,
DiscontinuitySearch = FALSE)):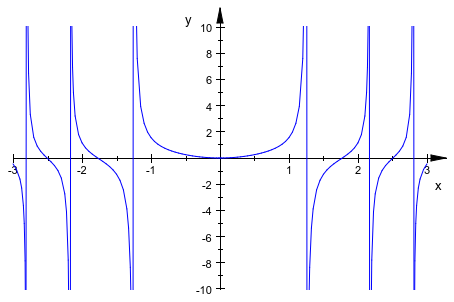
Без спецификации DiscontinuitySearch, настройка по умолчанию DiscontinuitySearch = TRUE используется. Побочные линии исчезают. С VerticalAsymptotesVisible = TRUE по умолчанию, они заменяются пунктирными вертикальными асимптотами, указывающими на полюса. Также обратите внимание, что числовая выборка около полюсов лучше, потому что существование сингулярности и их положений известно, прежде чем численная оценка функционального графика запускается:
plot(plot::Function2d(tan(x^2), x=-3..3,
ViewingBoxYRange = -10..10)):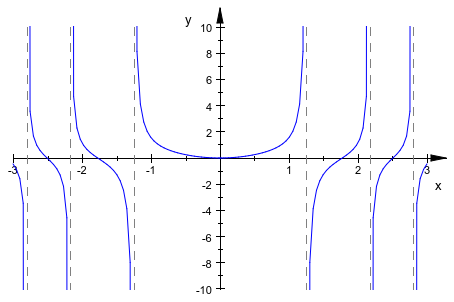
Функция Heaviside имеет разрыв скачка. Без поиска разрыва появляется побочная линия, соединяющая левые и правые предельные точки скачка:
plot(plot::Function2d(heaviside(x-1), x = -1..3,
DiscontinuitySearch = FALSE)):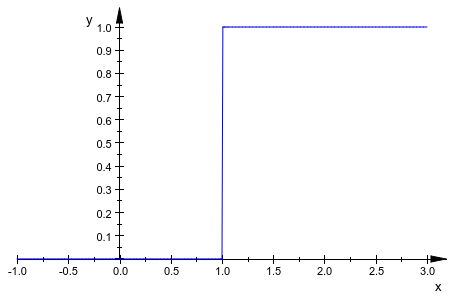
Эта побочная линия исчезает с настройкой по умолчанию DiscontinuitySearch = TRUE:
plot(plot::Function2d(heaviside(x-1), x = -1..3),
VerticalAsymptotesVisible = FALSE):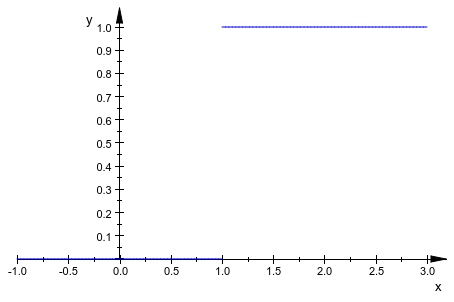
Без поиска разрыва полюса следующей сингулярной 3D кривой плохо представлены графически:
plot(plot::Curve3d([cos(u), sin(u), tan(2*u)], u = 0..2*PI,
ViewingBox = [-1..1, -1..1, -10..10],
DiscontinuitySearch = FALSE)):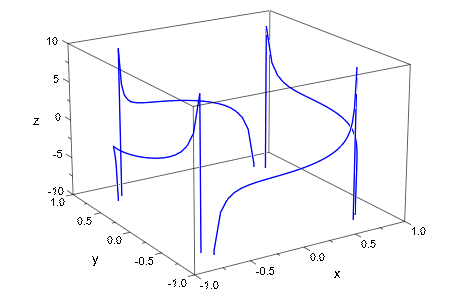
Настройка по умолчанию DiscontinuitySearch = TRUE производит лучшее графическое представление:
plot(plot::Curve3d([cos(u), sin(u), tan(2*u)], u = 0..2*PI,
ViewingBox = [-1..1, -1..1, -10..10])):