`plot`::`Function2d`

2D функциональные графики

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

plot::Function2d(f, options)
plot::Function2d(f, x = x_min .. x_max, <a = a_min .. a_max>, options)

Описание

plot::Function2d создает 2D график одномерной функции.

Графика игнорирует все точки, где выражение/функция f не производит числовое действительное значение. Смотрите Пример 2.

Выражение/функция f может иметь сингулярность в области значений графика. Несмотря на то, что эвристика используется, чтобы найти разумную область значений y, когда сингулярность присутствует, она настоятельно рекомендована, чтобы указать диапазон y через ViewingBoxYRange = `y_{min}` .. `y_{max}` с подходящими числовыми действительными значениями _ymin_ymax. Смотрите пример 3.

Анимации инициированы путем указания диапазона a = `a_{min}` .. `a_{max}` для параметра a это отличается от независимой переменной x. Таким образом, в анимациях, оба x - располагаются x = `x_{min}` .. `x_{max}` а также анимация располагается a = `a_{min}` .. `a_{max}` должен быть задан. Смотрите Пример 4.

Функциональный f оценен на равноотстоящей mesh точек выборки, определенных атрибутом XMesh (или краткое обозначение Mesh). По умолчанию, атрибут AdaptiveMesh = 0 установлен, т.е. никакое адаптивное улучшение равноотстоящей mesh не используется.

Если стандартная mesh не достаточна, чтобы произвести достаточно подробный график, можно или увеличить значение XMesh или набор AdaptiveMesh = n с некоторым (маленьким) положительным целочисленным n. При необходимости до 2ⁿ дополнительные точки помещаются между смежными точками начальной равноотстоящей mesh. Смотрите Пример 5.

По умолчанию, атрибут DiscontinuitySearch = TRUE установлен. Это инициировало полусимвольную предварительную обработку выражения f искать разрывы и сингулярность. В каждой особой точке функциональный график разделен в непересекающиеся ветви налево и справа от сингулярности. Это избегает графических артефактов, таких как соединительные точки линий налево и справа от сингулярности.

Если функция, как известно, является регулярной в области значений графика, полусимвольный поиск может быть отключен путем определения DiscontinuitySearch = FALSE. Это повысит эффективность команд plot.

Особые точки подсвечены вертикальной линией если VerticalAsymptotesVisible = FALSE задан. Его стиль может быть установлен атрибутами VerticalAsymptotesStyle, VerticalAsymptotesWidth, и VerticalAsymptotesColor.

Примечание

Эта функциональность только доступна, если функция задана арифметическое выражение или процедура, которая принимает символьные аргументы. Это не доступно, если функция задана piecewise возразите или процедурой, которая принимает только числовые аргументы.

Смотрите пример 6.

plot::Hatch позволяет штриховать области между функциональными графиками. Смотрите Пример 7.

Атрибуты

Атрибут	Цель	Значение по умолчанию
`AdaptiveMesh`	адаптивная выборка	2
`AffectViewingBox`	влияние объектов на `ViewingBox` из сцены	`TRUE`
`AntiAliased`	сглаженные линии и точки?	`TRUE`
`Color`	основной цвет	`RGB::Blue`
`DiscontinuitySearch`	полусимвольный поиск разрывов	`TRUE`
`Frames`	количество систем координат в анимации	50
`Function`	выражение function или процедура
`Legend`	делает запись легенды
`LegendText`	короткий объяснительный текст для легенды
`LegendEntry`	добавить этот объект в легенду?	`TRUE`
`LineColor`	цвет линий	`RGB::Blue`
`LineWidth`	ширина линий	0.35
`LineColor2`	цвет линий	`RGB::DeepPink`
`LineStyle`	тело, подчеркнутые штриховой линией или пунктирные линии?	`Solid`
`LinesVisible`	видимость линий	`TRUE`
`LineColorType`	типы окраски линии	`Flat`
`LineColorFunction`	функциональная окраска линии
`LineColorDirection`	направление цветовых переходов на линиях	[0, 1]
`LineColorDirectionX`	x-компонент направления цветовых переходов на линиях	0
`LineColorDirectionY`	y-компонент направления цветовых переходов на линиях	1
`Mesh`	количество точек выборки	121
`Name`	имя объекта графика (для браузера и легенды)
`ParameterEnd`	закончите значение параметра анимации
`ParameterName`	имя параметра анимации
`ParameterBegin`	начальное значение параметра анимации
`ParameterRange`	область значений параметра анимации
`PointSize`	размер точек	1.5
`PointStyle`	стиль презентации точек	`FilledCircles`
`PointsVisible`	видимость точек mesh	`FALSE`
`Submesh`	плотность подmesh (дополнительные точки выборки)	0
`TimeEnd`	время окончания анимации	10.0
`TimeBegin`	время начала анимации	0.0
`TimeRange`	оперативный промежуток анимации	0.0.. 10.0
`Title`	объектный заголовок
`TitleFont`	шрифт объектных заголовков	[`" sans-serif "`, 11]
`TitlePosition`	положение объектных заголовков
`TitleAlignment`	выравнивание по горизонтали заголовков w.r.t. их координаты	`Center`
`TitlePositionX`	положение объектных заголовков, x компонент
`TitlePositionY`	положение объектных заголовков, y компонент
`VerticalAsymptotesColor`	цвет вертикальных асимптот, указывающих на полюса	`RGB::Grey50`
`VerticalAsymptotesWidth`	ширина линии вертикальных асимптот, указывающих на полюса	0.2
`VerticalAsymptotesStyle`	стиль линии вертикальных асимптот, указывающих на полюса	`Dashed`
`VerticalAsymptotesVisible`	вертикальные асимптоты, указывающие на полюса	`TRUE`
`Visible`	видимость	`TRUE`
`VisibleAfter`	объект, видимый после этой временной стоимости
`VisibleBefore`	объект, видимый до этой временной стоимости
`VisibleFromTo`	объект, видимый в это время, располагается
`VisibleAfterEnd`	объект, видимый после его законченного времени анимации?	`TRUE`
`VisibleBeforeBegin`	объект, видимый перед его временем анимации, запускается?	`TRUE`
`XMax`	окончательное значение параметра “x”	5
`XMesh`	количество точек выборки для параметра “x”	121
`XMin`	начальное значение параметра “x”	-5
`XName`	имя параметра “x”
`XRange`	область значений параметра “x”	-5.. 5
`XSubmesh`	плотность дополнительных точек выборки для параметра “x”	0

Примеры

Пример 1

Следующий вызов возвращает объект, представляющий график синусоидальной функции на интервале [0, 2 π]:

f := plot::Function2d(sin(x), x = 0 .. 2*PI)

Вызовите plot построить график:

plot(f):

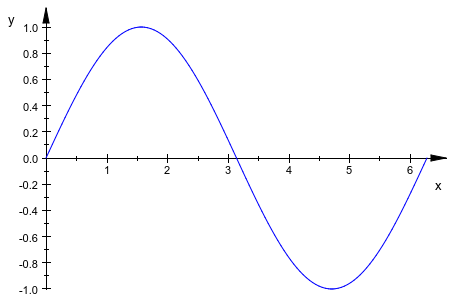
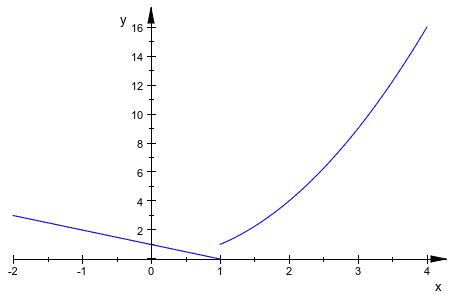
Функции могут также быть заданы piecewise объекты или процедуры:

f := piecewise([x < 1, 1 - x], [x >= 1, x^2]):
plot(plot::Function2d(f, x = -2 .. 4)):

f := proc(x)
begin
  if x^2 - 2*x < 0 then
     0
  else
     x^2 - 2*x
  end_if:
end_proc:
plot(plot::Function2d(f, x = -2 .. 4)):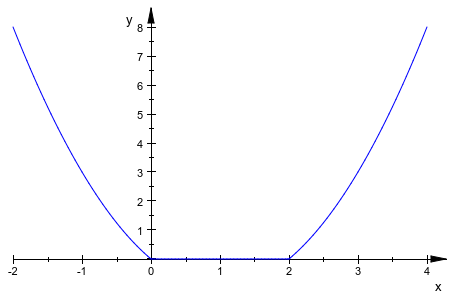

delete f:

Пример 2

Недействительные значения проигнорированы в графике:

plot(plot::Function2d(sqrt(1 - x^2), x = -2 .. 2),
     Scaling = Constrained):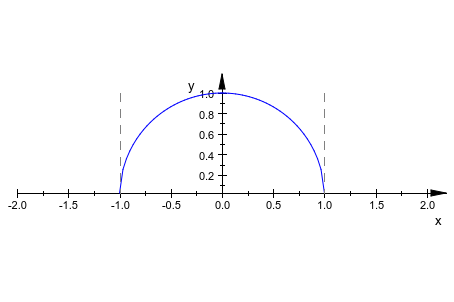

Пример 3

Мы строим функцию с сингулярностью:

f := plot::Function2d(sin(x)/(1 - x) - 1/cos(x), x = 0 .. PI):
plot(f):

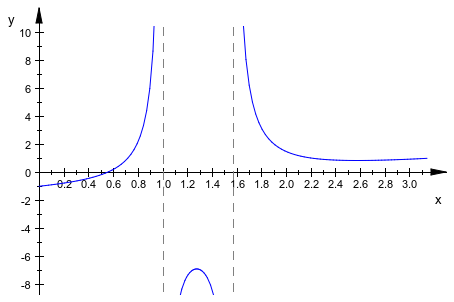
Мы указываем явный диапазон просмотра для направления y:

plot(f, ViewingBoxYRange = -20 .. 10):

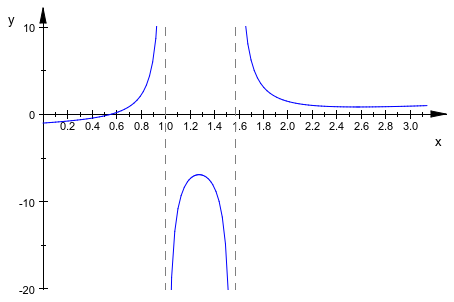
delete f:

Пример 4

Мы генерируем анимацию параметрической функции:

plot(plot::Function2d(a*sin(x) + (1 - a)*cos(x), 
                      x = -PI .. PI, a = 0 .. 1)):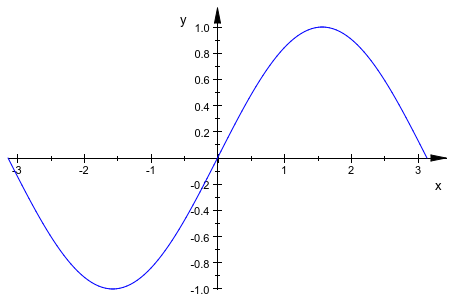

Пример 5

Стандартная mesh для численной оценки функционального графика не достаточна, чтобы сгенерировать удовлетворяющую графику в следующем случае:

plot(plot::Function2d(sin(PI/x), x = -1 .. 1)):

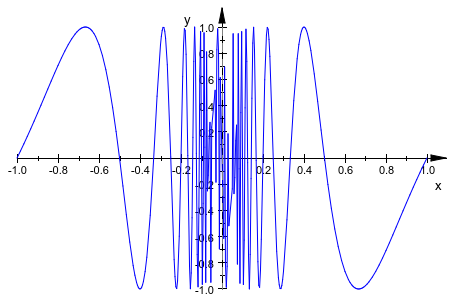
Мы увеличиваем число точек mesh:

plot(plot::Function2d(sin(PI/x), x = -1 .. 1, XMesh = 1000)):

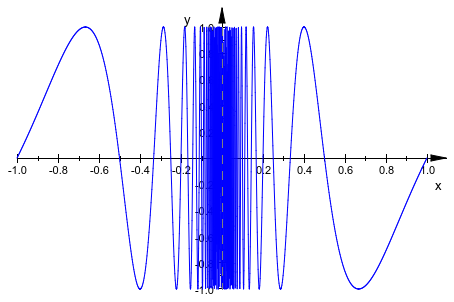
В качестве альтернативы мы включаем адаптивную выборку установкой AdaptiveMesh к некоторому положительному значению:

plot(plot::Function2d(sin(PI/x), x = -1 .. 1, AdaptiveMesh = 3)):

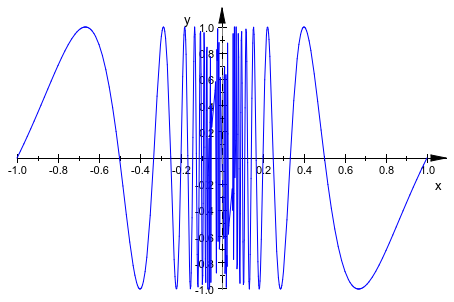
Наконец, мы увеличиваем XMesh значение и адаптивная выборка использования:

plot(plot::Function2d(sin(PI/x), x = -1 .. 1, XMesh = 1000,
                      AdaptiveMesh = 3)):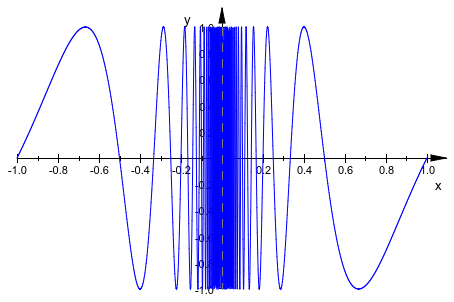

Пример 6

С VerticalAsymptotesVisible = TRUE/FALSE, особые точки подсвечены вертикальной асимптотой, или это выделение выключено, соответственно:

plot(plot::Function2d(ln(x + PI) + 1/(x - 1) - 1/(x + 1)^2,
                      x = -4 .. 4, 
                      VerticalAsymptotesVisible = TRUE,
                      ViewingBoxYRange = -10 .. 10)):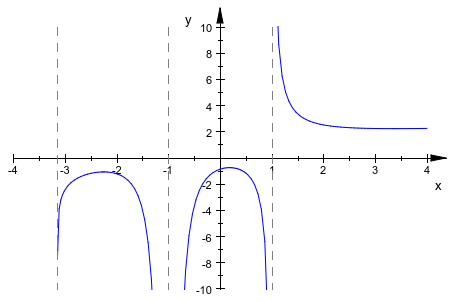

plot(plot::Function2d(ln(x + PI) + 1/(x - 1) - 1/(x + 1)^2,
                      x = -4 .. 4, 
                      VerticalAsymptotesVisible = FALSE,
                      ViewingBoxYRange = -10 .. 10)):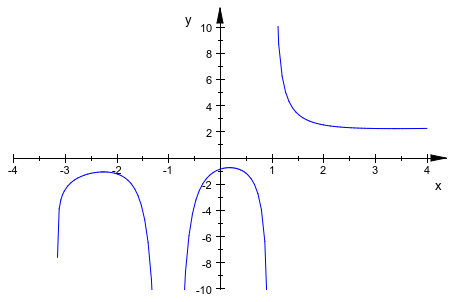

Пример 7

plot::Hatch объект позволяет штриховать области между функциями. Это ожидает графические объекты типа plot::Function2d или plot::Curve2d как контуры:

f1:= plot::Function2d(sin(x), x = -PI .. 2*PI):
f2:= plot::Function2d(cos(x), x = -PI .. 2*PI):
plot(f1, f2, plot::Hatch(f1, f2, -1 .. 5)):

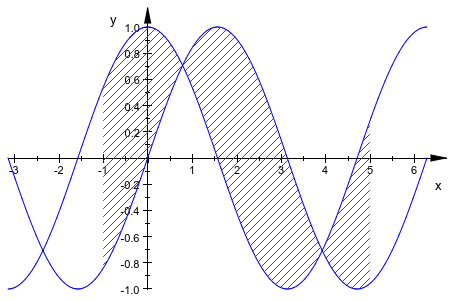
delete f1, f2:

Параметры

`f`	Функция: арифметическое выражение или `piecewise` объект в независимой переменной x и параметр анимации a. В качестве альтернативы процедура, которая принимает 1 входной параметр x или 2 входных параметра x, a и возвращает действительное численное значение, когда входные параметры являются числовыми. `f` эквивалентно атрибуту `Function`.
`x`	Независимая переменная: идентификатор или индексируемый идентификатор. `x` эквивалентно атрибуту `XName`.
`_{xmin .. xmax}`	Область значений графика: `_xmin_xmax` должны быть числовые действительные значения или выражения параметра анимации a. Если не заданный, область значений по умолчанию `x = -5 .. 5` используется. `_xmin` `_xmax` эквивалентно атрибутам `XRangexmin` `xmax` .
`a`	Параметр анимации, заданный как `a` `_{= amin..amax}`, где `_amin` начальное значение параметров и `_amax` итоговое значение параметров.

Документация