plot::Curve2dПараметризованные 2D кривые
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
plot::Curve2d([x, y],t = tmin .. tmax, <a = amin .. amax>,options) plot::Curve2d(A2d,t = tmin .. tmax, <a = amin .. amax>,options) plot::Curve2d(piecewiseF(t),t = tmin .. tmax, <a = amin .. amax>,options)
plot::Curve2d([x(t), y(t)], t = tmin.. tmax) создает плоскую кривую
![]() .
.
plot::Curve2d графики изгибаются в одном параметре. Смотрите Пример 1,
Можно использовать его, чтобы построить анимированные кривые. Смотрите Пример 2.
Кривые могут содержать полюса, в этом случае автоматическое усечение используется по умолчанию. Смотрите Пример 4.
По умолчанию кривые производятся в равноотстоящих значениях параметра t. Чтобы изменить это поведение так, чтобы более плотный уровень выборки использовался в областях высшей кривизны, используйте атрибут AdaptiveMesh. Смотрите пример 5.
Кривые являются графическими объектами, которыми можно управлять. Смотрите примеры и документацию для атрибутов для деталей.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AdaptiveMesh | адаптивная выборка | 0 |
AffectViewingBox | влияние объектов на ViewingBox из сцены | TRUE |
AntiAliased | сглаженные линии и точки? | TRUE |
Color | основной цвет | RGB::Blue |
DiscontinuitySearch | полусимвольный поиск разрывов | TRUE |
Frames | количество систем координат в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | TRUE |
LineColor | цвет линий | RGB::Blue |
LineWidth | ширина линий | 0.35 |
LineColor2 | цвет линий | RGB::DeepPink |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость линий | TRUE |
LineColorType | типы окраски линии | Flat |
LineColorFunction | функциональная окраска линии | |
LineColorDirection | направление цветовых переходов на линиях | [0 |
LineColorDirectionX | x-компонент направления цветовых переходов на линиях | 0 |
LineColorDirectionY | y-компонент направления цветовых переходов на линиях | 1 |
Mesh | количество точек выборки | 121 |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
PointSize | размер точек | 1.5 |
PointStyle | стиль презентации точек | FilledCircles |
PointsVisible | видимость точек mesh | FALSE |
Submesh | плотность подmesh (дополнительные точки выборки) | 0 |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11 |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
UMax | окончательное значение параметра “u” | 5 |
UMesh | количество точек выборки для параметра “u” | 121 |
UMin | начальное значение параметра “u” | -5 |
UName | имя параметра “u” | |
URange | область значений параметра “u” | -5 |
USubmesh | плотность дополнительных точек выборки для параметра “u” | 0 |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
XFunction | функция для x значений | |
YFunction | функция для y значений |
Спираль Archimedes задана f (r) = (r sin (r), r cos (r)). Соответствующий вызов plot::Curve2d чтения:
curve := plot::Curve2d([r*sin(r), r*cos(r)], r = 0..35)
![]()
plot(curve)
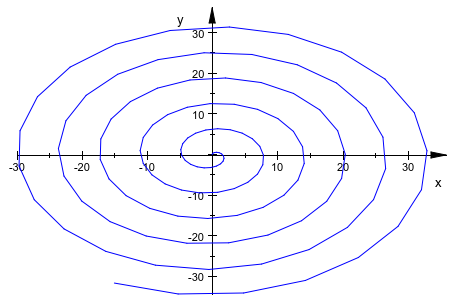
Обратите внимание на то, что этот конкретный пример является еще более прямым, чтобы построить использование plot::Polar.
При продолжении примера сверху, задайте легкую анимацию путем создания угловой части зависящей от времени:
curve := plot::Curve2d([r*sin(r-t), r*cos(r-t)],
r = 0..35, t = 0..2*PI,
TimeEnd = 5,
ViewingBox = [-25..25, -25..25]):
plot(curve)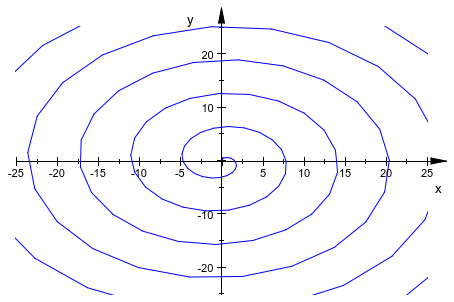
Обратите внимание на то, что, чтобы запустить анимацию, необходимо дважды кликнуть изображение в блокноте и выбрать "Start" из меню “Animation”.
Другой полезный и легкий тип анимации достигается путем анимации области значений параметра. Это создает иллюзию кривой, чертившей в режиме реального времени:
curve := plot::Curve2d([sin(thet), cos(thet)],
thet = 0..a,
a = 0..2*PI):
plot(curve)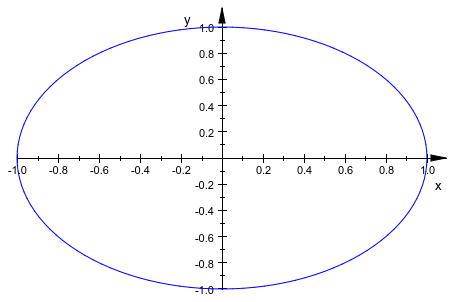
Объединение этого с анимированным LineColorFunction, можно даже симулировать движение:
colorfunc := (thet, x, y, a) -> [a-thet, a-thet, 1.0]:
curve := plot::Curve2d([sin(3*thet), sin(4*thet)],
thet = a-1..a,
LineColorFunction = colorfunc,
LineWidth = 1,
a = 0..2*PI):
plot(curve)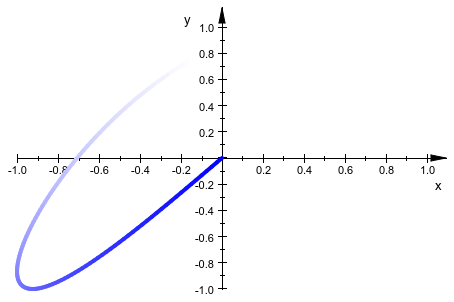
Кривые с полюсами автоматически отсекаются:
curve := plot::Curve2d([(1+tan(3*t)^2)*sin(t),
(1+tan(3*t)^2)*cos(t)],
t = 0..2*PI):
plot(curve);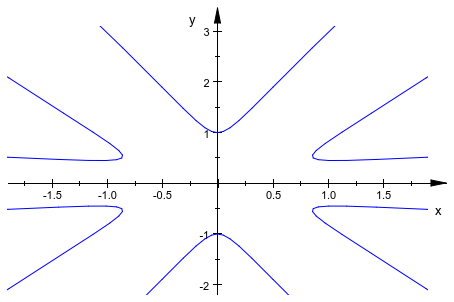
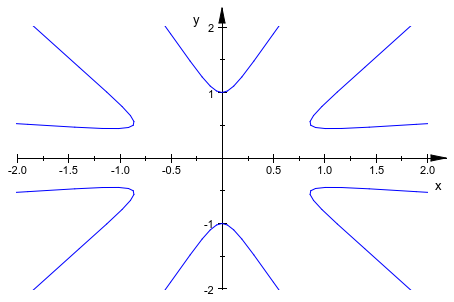
Можно явным образом установить другие значения для просмотра поля:
curve::ViewingBox := [-2..2, -2..2]: plot(curve)
По умолчанию кривые чертятся путем оценки в равноотстоящих значениях параметра кривой. Для кривых, которые имеют немного областей высокого искривления, это может быть несоответствующим:
plot(plot::Curve2d([arctan(t), t^2-10*exp(-50*t^2)],
t = -PI..PI))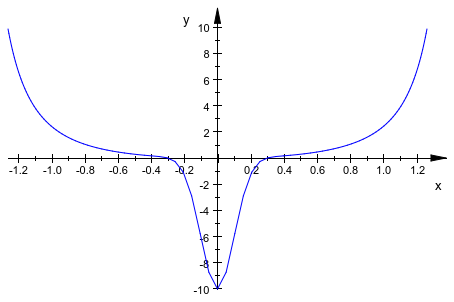
Отметьте твердую “петлю” в нижней части изображения. С другой стороны, остаток от кривой достаточно является гладким, таким образом, глобально увеличение числа точек оценки не желательно. AdaptiveMesh делает plot::Curve2d ищите эти петли и адаптивно повысьте плотность mesh в проблематичных областях:
plot(plot::Curve2d([arctan(t), t^2-10*exp(-50*t^2)],
t = -PI..PI, AdaptiveMesh = 2))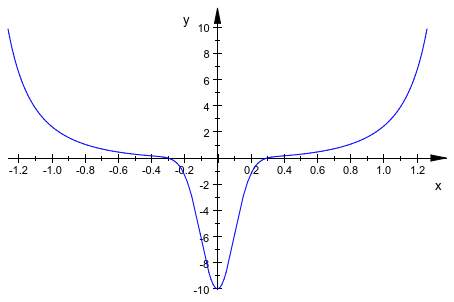
Чтобы отобразить кривую в комплексной плоскости, сопоставьте функциональный [Re, Im] со знаком списка к кривой:
plot(plot::Curve2d([Re, Im](zeta(I*y+1/2)), y=0..42,
AdaptiveMesh=3),
XAxisTitle = "Re(z)", YAxisTitle = "Im(z)")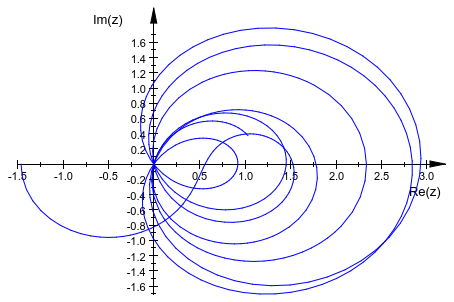
|
Выражения с действительным знаком в |
|
Матрица A категории |
|
|
| |
|
Выражения с действительным знаком (возможно в параметре анимации) |
|
Параметр анимации, заданный как |