numeric::odesolveЧисловое решение обыкновенного дифференциального уравнения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
numeric::odesolve(f,t0 .. t,Y0, <method>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <MaxStepsize = hmax>, <Alldata = n>, <Symbolic>) numeric::odesolve(t0 .. t,f,Y0, <method>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <MaxStepsize = hmax>, <Alldata = n>, <Symbolic>)
numeric::odesolve(f, t0..t, Y0) возвращает числовое приближение решения Y (t) дифференциального уравнения первого порядка (динамическая система)
, Y (t 0) = Y 0 с
и
.
numeric::odesolve решатель общего назначения, который в состоянии иметь дело с задачами с начальными значениями различных видов обыкновенных дифференциальных уравнений. Уравнения
порядка p могут быть решены numeric::odesolve после переформулировки к динамической системной форме. Это может всегда достигаться путем записи уравнения как системы первого порядка
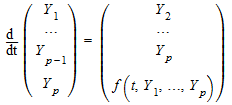
для вектора
. Смотрите Пример 4.
Следующие одноступенчатые методы Типа Рунге-Кутта реализованы:
EULER1 (порядок 1)
RKF43 (порядок 3)
xRKF43 (порядок 3)
RKF34 (порядок 4)
xRKF34 (порядок 4)
RK4 (порядок 4)
RKF54a (порядок 4)
RKF54b (порядок 4)
DOPRI54 (порядок 4)
xDOPRI54 (порядок 4)
CK54 (порядок 4)
xRKF54a (порядок 4)
xRKF54b (порядок 4)
xCK54 (порядок 4)
RKF45a (порядок 5)
RKF45b (порядок 5)
DOPRI45 (порядок 5)
CK45 (порядок 5)
xRKF45a (порядок 5)
xRKF45b (порядок 5)
xDOPRI45 (порядок 5)
xCK45 (порядок 5)
DOPRI65 (порядок 5)
xDOPRI65 (порядок 5)
DOPRI56 (порядок 6)
xDOPRI56 (порядок 6)
BUTCHER6 (порядок 6)
RKF87 (порядок 7)
xRKF87 (порядок 7)
DOPRI87 (порядок 7)
xDOPRI87 (порядок 7)
RKF78 (порядок 8)
xRKF78 (порядок 8)
DOPRI78 (порядок 8)
xDOPRI78 (порядок 8)
GAUSS(s) (порядок 2 s)
GAUSS = s
Для методов Гаусса, GAUSS(s) эквивалентно GAUSS = s. Положительный целочисленный s указывает на количество этапов. Порядок s метод Гаусса этапа 2 s.
Служебная функция numeric::ode2vectorfield может использоваться, чтобы произвести входные параметры f, t 0, Y 0 от набора дифференциальных выражений, представляющих ОДУ. Смотрите Пример 1.
0 t входных данных, t и Y, 0 не должен содержать символьные объекты, которые не могут быть преобразованы в значения с плавающей точкой через float. Числовые выражения такой как
,
и т.д. приняты.
Векторное поле f, задающее динамическую систему
, должно быть представлено процедурой двумя входными параметрами: скалярное время t и векторный Y. numeric::odesolve внутренне вызывает эту функцию с действительными значениями с плавающей точкой t и список Y значений с плавающей точкой. Это должно возвратить векторный f (t, Y) или как список или как 1-мерный массив. Выход f может содержать числовые выражения, такие как π
и т.д. Однако все значения должны быть конвертируемыми к действительным или комплексным числам с плавающей точкой float.
Автономные системы, где f (t, Y) не зависит от t, должны также быть представлены процедурой с 2 аргументами t и Y.
Скалярные функции Y также должен быть представлен списком или массивом с одним элементом. Например, входные данные для скалярной задачи с начальными значениями
могут иметь форму
f := proc(t,Y) | /* Y является 1-мерным вектором */ |
local y; | /* представленный списком с */ |
begin | /* один элемент: Y = [y]. */ |
y := Y[1]; | |
[t*sin(y)] | /* выход является списком с 1 элементом */ |
end_proc: | |
Y0 := [1]: | /* начальное значение */ |
Числовой точностью управляет глобальная переменная DIGITS: адаптивное управление размера шага сохраняет локальные относительные ошибки дискретизации ниже rtol=10^-DIGITS, если различный допуск не задан с помощью опции RelativeError = rtol. Для маленьких значений вектора решения Y абсолютная ошибка дискретизации может быть ограничена порогом atol заданный с помощью опции AbsoluteError = atol.
Если AbsoluteError не задан, только относительными ошибками дискретизации управляют и сохраняют ниже rtol.
Контроль ошибок может быть выключен путем определения фиксированного Stepsize = h.
Только локальными ошибками управляет адаптивный механизм. Никакое управление глобальной ошибки не обеспечивается!
С Y := t -> numeric::odesolve(f, t_0..t, Y_0), числовое решение может быть repesented функцией MuPAD®: вызов Y(t) запустит численное интегрирование с t0 к t. Более сложная форма этой функции может быть сгенерирована через Y := numeric::odesolve2(f, t0, Y0).
Это оборудует Y с помнить механизмом, который использует ранее вычисленные значения, чтобы ускорить расчет. Смотрите Пример 2.
Для систем специальной формы
с матрицей оцененный функциональный f (t, Y), существует специальный решатель numeric::odesolveGeometric который сохраняет геометрические функции системы более искренне, чем numeric::odesolve.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы вычисляем числовое решение y (10) из задачи с начальными значениями
, y (0) = 2:
f := proc(t, Y) begin [t*sin(Y[1])] end_proc: numeric::odesolve(f, 0..10, [2])
В качестве альтернативы служебная функция numeric::ode2vectorfield может использоваться, чтобы сгенерировать входные параметры более интуитивным способом:
[f, t0, Y0] :=
[numeric::ode2vectorfield({y'(t) = t*sin(y(t)), y(0) = 2}, [y(t)])]
numeric::odesolve(f, t0..10, Y0)
delete f, t0, Y0:
Мы рассматриваем
, y (0) = 1. Числовое решение может быть представлено функцией
Y := t -> numeric::odesolve((t,Y) -> Y, 0..t, [1]):
Вызов Y(t) запускает численное интегрирование:
Y(-5), Y(0), Y(1), Y(PI)
delete Y:
Мы вычисляем числовое решение Y (π) = [x (π), y (π)] системы
.
f := (t, Y) -> [Y[1] + Y[2], Y[1] - Y[2]]: Y0 := [1, I]: numeric::odesolve(f, 0..PI, Y0)
Решение линейной динамической системы
с постоянным матричным A
. Решение системы выше может также быть вычислено:
t := PI: tA := array(1..2, 1..2, [[t, t], [t, -t]]): numeric::expMatrix(tA, Y0)
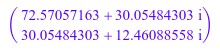
delete f, Y0, t, tA:
Мы вычисляем числовое решение y (1) из дифференциального уравнения
с начальными условиями y (0) = 0
. Уравнение второго порядка преобразовано в систему первого порядка для вектора
:
.
f := proc(t, Y) begin [Y[2], Y[1]^2] end_proc: Y0 := [0, 1]: numeric::odesolve(f, 0..1, Y0)
delete f, Y0:
Мы демонстрируем, как числовые данные могут быть получены на определяемой пользователем mesh времени t[i]. Задача с начальными значениями
, y (0) = 1, точками выборки является t 0 = 0.0, t 1 = 0.1, …, t 100 = 10.0. Во-первых, мы определяем дифференциальное уравнение и начальное условие:
f := (t, Y) -> [sin(t) - Y[1]]: Y[0] := [1]:
Мы задаем mesh времени:
for i from 0 to 100 do t[i] := i/10 end_for:
Уравнение интегрировано итеративно от t[i-1] к t[i] с рабочей точностью 4 значительных десятичных разрядов:
DIGITS := 4: for i from 1 to 100 do Y[i] := numeric::odesolve(f, t[i-1]..t[i], Y[i-1]) end_for:
Следующие данные о mesh производятся:
[t[i], Y[i]] $ i = 0..100
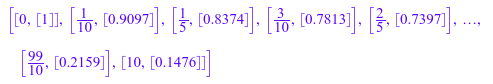
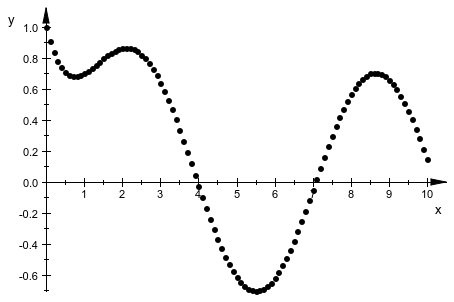
Эти данные могут быть отображены графиком списка:
plotpoints := [[t[i], op(Y[i])] $ i = 0..100]: plot(plot::PointList2d(plotpoints, PointColor = RGB::Black)):
Тот же график может быть получен непосредственно через plot::Ode2d:
plot(plot::Ode2d(
[t[i] $ i = 0..100], f, Y[0],
[(t, Y) -> [t, Y[1]], Style = Points, Color = RGB::Black]))
delete f, t, DIGITS, Y, plotpoints:
Мы вычисляем числовое решение y (1) из
классическим 4-м Методом Рунге-Кутта порядка RK4. Внутренней локальной экстраполяцией ее эффективный порядок равняется 5:
f := (t, Y) -> Y: DIGITS := 13: numeric::odesolve(f, 0..1, [1], RK4)
Затем мы используем локальную экстраполяцию xRKF78 из 8-го подметода порядка парного RKF78 Runge-Kutta-Fehlberg. Эта схема имеет эффективный порядок 9:
numeric::odesolve(f, 0..1, [1], xRKF78)
Оба метода дают к тому же результату из-за внутреннего адаптивного контроля ошибок. Однако из-за его высшего порядка, метод xRKF78 быстрее.
delete f, DIGITS:
Мы рассматриваем жесткое ОДУ
. Метод по умолчанию DOPRI78 является явным и не очень эффективным в решении очень жестких задач:
f := (t, Y) -> [10^4*(cos(t) - Y[1])]: t0 := time(): numeric::odesolve(f, 0..1, [1]), (time() - t0)*msec
Мы используем неявный Неустойчивый метод GAUSS(6). Для этой жесткой проблемы это более эффективно, чем метод по умолчанию DOPRI78:
t0 := time(): numeric::odesolve(f, 0..1, [1], GAUSS(6)), (time() - t0)*msec
delete t0:
Мы рассматриваем задачу с начальными значениями
, y (0) = 1. Мы отмечаем, что численная оценка правой стороны уравнения страдает от эффектов отмены, когда |y | мал.
f := (t, Y) -> [-10^20*Y[1]*(1 - cos(Y[1]))]: Y0 := [1]:
Мы сначала пытаемся вычислить y (1) с рабочей точностью 6 цифр с помощью настройки по умолчанию RelativeError = 10^-DIGITS=10^(-6):
DIGITS := 6: numeric::odesolve(f, 0..1, Y0)
Из-за числового округления на внутренних шагах, никакая цифра этого результата не правильна. Затем мы используем рабочую точность 20 значительных десятичных разрядов, чтобы устранить эффекты округления:
DIGITS := 20: numeric::odesolve(f, 0..1, Y0, RelativeError = 10^(-6))
Поскольку относительные локальные ошибки дискретизации имеют величину 10 - 6, не, все отображенные цифры защищены. Мы наконец используем рабочую точность 20 цифр и ограничиваем локальные относительные ошибки дискретизации допуском 10 - 10:
numeric::odesolve(f, 0..1, Y0, RelativeError = 10^(-10))
delete f, Y0, DIGITS:
Мы вычисляем числовое решение y (1) из
, y (0) = 1 с различными методами и различными постоянными размерами шага. Мы сравниваем результат с точным решением
.
f := (t, Y) -> Y: Y0 := [1]:
Мы сначала используем Метод Эйлера порядка 1 с двумя различными размерами шага:
Y := numeric::odesolve(f, 0..1, Y0, EULER1, Stepsize = 0.1): Y, globalerror = float(exp(1)) - Y[1]
Уменьшение размера шага фактором 10 должно уменьшать глобальную ошибку фактором 10. Действительно:
Y := numeric::odesolve(f, 0..1, Y0, EULER1, Stepsize = 0.01): Y, globalerror = float(exp(1)) - Y[1]
Затем мы используем классический Метод Рунге-Кутта порядка 4 с двумя различными размерами шага:
Y := numeric::odesolve(f, 0..1, Y0, RK4, Stepsize = 0.1): Y, globalerror = float(exp(1)) - Y[1]
Уменьшение размера шага фактором 10 в 4-й схеме порядка должно уменьшать глобальную ошибку фактором 104. Действительно:
Y := numeric::odesolve(f, 0..1, Y0, RK4, Stepsize = 0.01): Y, globalerror = float(exp(1)) - Y[1]
delete f, Y0, Y:
Мы объединяемся
, y (0) = 1 на интервале t ∈ [0, 0.99] с рабочей точностью 4 цифр. Точное решение
. Отметьте сингулярность в t = 1.
DIGITS := 4: f := (t, Y) -> [Y[1]^2]: Y0 := [1]:
Опция Alldata, эквивалентный Alldata = 1, урожаи все данные о mesh сгенерировали во время внутреннего адаптивного процесса:
numeric::odesolve(f, 0..0.99, Y0, Alldata)
С Alldata = 2, только каждая вторая точка возвращена:
numeric::odesolve(f, 0..0.99, Y0, Alldata = 2)
Можно управлять mesh времени с помощью опции Stepsize = h:
numeric::odesolve(f, 0..0.99, Y0, Stepsize=0.1, Alldata = 1)
Однако с опцией Stepsize = h, никакой автоматический контроль ошибок не обеспечивается numeric::odesolve. Отметьте плохое приближение y (t) = 94.3 для t = 0.99 (точным значением является y (0.99) = 100.0). Следующий расчет с меньшим размером шага дает к лучшим результатам:
numeric::odesolve(f, 0..0.99, Y0, Stepsize = 0.01, Alldata = 10)
Пример 5 демонстрирует, как точные числовые данные по определяемой пользователем mesh времени могут быть сгенерированы с помощью автоматического контроля ошибок numeric::odesolve.
delete DIGITS, f, Y0:
Уравнение второго порядка
записано как динамическая система
,
для векторного Y = [y, z]. Один символьный шаг
из Метода Эйлера вычисляется:
f := proc(t, Y) begin [Y[2], -sin(Y[1])] end_proc: numeric::odesolve(f, t0..t0+h, [y0, z0], EULER1, Symbolic)
delete f:
|
Процедура, представляющая векторное поле |
|
Числовое действительное значение в течение начального времени |
|
Числовое действительное значение (“время”) |
|
Список или 1-мерный массив численных значений, представляющих начальное условие |
|
Одна из схем Runge-Kutta описана ниже. |
|
Имя схемы Runge-Kutta. Смотрите Пример 6. Для получения дополнительной информации на этих схемах, смотрите раздел Algorithms. |
|
Имя схемы Runge-Kutta, заданной как Методы Эти методы являются неявными Неустойчивыми схемами. Временные шаги являются довольно дорогостоящими, чтобы вычислить. Методы Гаусса полезны для интеграции жестких ОДУ. Для нежестких ОДУ обычно нет никакой потребности изменить метод по умолчанию Далее, методы Гаусса являются симплектическими методами. Когда используется с постоянным размером шага ( Смотрите пример 7. |
|
Опция, заданная как Опция, заданная как Механизм внутреннего контроля оценивает локальную ошибку дискретизации шага Рунге-Кутта и настраивает размер шага адаптивно, чтобы сохранить эту ошибку ниже заданных допусков
Для принятия вектора решения Y. Примерно говоря, относительной погрешностью управляют, когда решение Y является достаточно большим. Для очень маленьких значений решения Y абсолютные ошибки дискретизации сохранены ниже порога Задайте Контроль ошибок может быть выключен путем определения фиксированного Настройка по умолчанию Обычно нет никакой потребности использовать эти опции, чтобы изменить эти настройки. Однако иногда численная оценка шагов Рунге-Кутта может быть плохо обусловлена или продвинуться, размеры так малы, что параметр времени не может быть постепенно увеличен размером шага в рабочей точности. В таком случае эти опции могут использоваться к связанному локальные ошибки дискретизации и использовать более высокую рабочую точность, данную Только положительные действительные численные значения ПримечаниеГлобальная ошибка результата возвращена Смотрите пример 8. |
|
Опция, заданная как Выключает внутренний контроль ошибок и использует итерацию Рунге-Кутта с постоянным размером шага По умолчанию, Последний шаг с меньшим размером шага используется, чтобы совпадать с концом ПримечаниеПри использовании этой опции нет никакого автоматического контроля ошибок! В зависимости от проблемы и на порядке метода результатом может быть плохое числовое приближение точного решения. Обычно нет никакой потребности вызвать эту опцию. Однако иногда встроенный адаптивный механизм контроля ошибок может перестать работать при интеграции близко к сингулярности. В таком случае эта опция может использоваться, чтобы настроить механизм управления для глобальной ошибки при помощи различных размеров шага и исследования сходимости соответствующих результатов. См. пример 9. |
|
Опция, заданная как Ограничивает адаптивные размеры шага значениями, не больше, чем По умолчанию, Если больший stepsize |
|
Опция, заданная как Делает При использовании этой опции, Целочисленный Список выходов может быть полезным, чтобы смотреть внутренний числовой процесс. Также дальнейшая графическая обработка данных о mesh может быть полезной. См. пример 10. |
|
Делает Вызов Эта опция может быть полезной, если бы заданный численный метод применился к данному дифференциальному уравнению, то должен быть исследован символически. См. пример 11. |
Вектор решения Y (t) возвращен как список или как 1-мерный массив значений с плавающей точкой. Тип итогового вектора совпадает с типом входного вектора Y0.
С опцией Alldata, список данных о mesh возвращен.
Дж.К. Бучер: “Числовой анализ Обыкновенных дифференциальных уравнений”, Вайли, Чичестер (1987).
Э. Хэрер, С.П. Норсетт и G. Более бледный: “Решая Обыкновенные дифференциальные уравнения I”, Спрингер, Берлин (1993).
Все методы, в настоящее время реализованные, являются адаптивными версиями типа Рунге-Кутта одна схемы шага.
Методы RKF43, RKF34, RKF54a, RKF54b, RKF45a, RKF45b, RKF87, RKF78, DOPRI54, DOPRI45, DOPRI65, DOPRI56, DOPRI87, DOPRI78, CK54, CK45 встроенные пары Рунге-Кутта-Фельберга, Dormand-принца и Наличного-Karp типа, соответственно. Оценки локальной ошибки дискретизации получены обычным способом путем сравнения результатов двух подметодов пары. Имена указывают на порядки подпроцессов. Например, RKF34 и RKF43 обозначьте, что то же самое встроило пару Runge-Kutta-Fehlberg с порядками 3 и 4. В RKF34 результат четвертого подметода порядка принят, тогда как RKF43 усовершенствования с помощью результата третьего подметода порядка. В обоих случаях ошибку дискретизации подпроцесса более низкоуровневого оценивают и управляют.
Для отдельных методов EULER1 (первый порядок схема Эйлера), RK4 (классический четвертый порядок схема Runge-Kutta) и BUTCHER6 (схема Runge-Kutta порядка 6), относительной локальной ошибкой управляют путем сравнения шагов с различными размерами шага. Эффективный порядок этих методов увеличен на один посредством локальной экстраполяции.
Локальная экстраполяция также доступна для подметодов встроенных пар. Например, метод xRKF78 экстраполяция использования 8-го подпроцесса порядка RKF78, получение метода эффективного порядка 9. 7-й подпроцесс порядка проигнорирован. Дешевая ошибочная оценка на основе встроенной пары не используется, подразумевая некоторое снижение эффективности при сравнении RKF78 (порядок 8) и xRKF78 (эффективный порядок 9).
Вызов numeric::butcher(method) возвращает данные Мясника методов, используемых в numeric::odesolve. Здесь method один из EULER1, RKF43, RK4, RKF34, RKF54a, RKF54b, DOPRI54, CK54, RKF45a, RKF45b, DOPRI45, CK45, DOPRI65, DOPRI56, BUTCHER6, RKF87, DOPRI87, RKF78, DOPRI78.
Только локальными ошибками управляет адаптивный механизм. Никакое управление глобальной ошибки не обеспечивается!
Время выполнения численного интегрирования с методом порядка p растет как
, когда DIGITS увеличен. Расчеты с целями высокой точности являются очень дорогими! Высокого уровня методы, такие как метод по умолчанию DOPRI78 должен использоваться.
В настоящее время только один методы шага типа Рунге-Кутта реализованы. Жесткие проблемы не могут быть решены эффективно с явными методами, такими как метод по умолчанию DOPRI78. Для жестких проблем можно использовать один из неявных Неустойчивых методов GAUSS(s). Смотрите пример 7.
Для проблем специального типа
с матрицей оцененный функциональный f (t, Y), существует специализированная (“геометрическая”) стандартная программа интегрирования numeric::odesolveGeometric. Обычно numeric::odesolve быстрее, чем геометрический интегратор. Однако odesolveGeometric сохраняет определенные инварианты системы более искренне.
