`numeric`::`odesolveGeometric`

Числовое решение обыкновенного дифференциального уравнения на гомогенном коллекторе

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

numeric::odesolveGeometric(f, t₀ .. t, Y₀, <LieGroupAction = LAMBDA>, <method>, <RelativeError = tol>, <Stepsize = h>, <Alldata = n>)
numeric::odesolveGeometric(t0 .. t, f, Y₀, <LieGroupAction = LAMBDA>, <method>, <RelativeError = tol>, <Stepsize = h>, <Alldata = n>)

Описание

numeric::odesolveGeometric(f, t_0..t, Y_0 ) аппроксимирует решение, куда f (t, Y (t)) возвращает n ×n матрицы и.

numeric::odesolveGeometric “геометрический интегратор” для обыкновенных дифференциальных уравнений на гомогенных коллекторах, встроенных в течение n ×m матрицы.

Вызов numeric::odesolveGeometric(f, t_0..t, Y_0 ) возвращает числовое приближение решения Y (t) дифференциального уравнения первого порядка (динамическая система)

с. Здесь, Y (t) является кривой n ×m матрицы (или векторы в или). Функциональный f должен произвести n ×n матрицы как возвращаемые значения.

Следующая геометрическая функция сохраняется числовым решением: Если матрицы, произведенные f, лежат в некоторой подалгебре Ли g n ×n матрицы, то, в числовой рабочей точности, приближение, произведенное numeric::odesolveGeometric остается на гомогенном коллекторе, где G является матричной группой Ли g.

Как вводный пример, рассмотрите ОДУ, где Y является вектором в и f производит скошенные симметричные матрицы. Решение находится на орбите ортогональной группы SO (n), сгенерированный скошенными симметричными матрицами через начальную точку. Здесь, SO (n) действует на стандартным умножением матриц. Гомогенный коллектор, данный орбитой SO (n) через Y ₀, является сферой

Используя стандартные числовые схемы, числовое решение дрейфует далеко от этого коллектора в ходе интегрирования. Геометрический интегратор “группы Ли” numeric::odesolveGeometric, однако, производит числовое решение, которое остается на этом коллекторе, сохраняя инварианты действий группы. В этом случае инвариант сохраняется численно. Смотрите Пример 1.

С Y (t) = G (t) Y₀, матричное ОДУ

решен на пробеле комплексного n ×n матрицы (1_{n, n} является единичной матрицей). Следующая Манзэ-Каас [1], подход уменьшает временной шаг для оды выше к решению матричного ОДУ

где и [u, f] = u f - f u является коммутатором на алгебре Ли n ×n матрицы. На каждом шаге ОДУ для u решен численно классическим способом схемой Runge-Kutta, заданной параметром method. Наконец, numeric::odesolveGeometric выполняет временной шаг путем вычисления.

Если матрицы, произведенные f (t, Y), лежат в подалгебре Ли g n ×n матрицы, то числовое решение u также находится в g. Матрица является элементом соответствующей группы Ли и Y = G, Y₀ находится на орбите группы Ли через начальное значение Y ₀. Таким образом геометрические инварианты гомогенного коллектора сохраняются в ходе численного интегрирования.

₀ t входных данных и t не должны содержать символьные объекты, которые не могут быть преобразованы в значения с плавающей точкой через float. Числовые выражения такой как, и т.д. приняты.

Начальный ₀ Y условия задает пробел, в который встраивается гомогенный коллектор, содержащий решение.

Если Y ₀ является списком с записями n или 1-мерным массивом array(1..n), затем решение Y (t) состоит из векторов от подколлектора или, соответственно.

Если Y ₀ задан как 2-мерный array(1..n, 1..m) или когда матрица соответствующей размерности сгенерирована функциональным matrix, затем решение Y (t) состоит из матриц от подколлектора пробела n ×m матрицы.

Внутренне, 2-мерный n ×m массивы используется, чтобы представлять точки на коллекторе где m = 1 для векторов в или. Рекомендуется задать Y ₀ в форме array(1..n, 1..m) во избежание издержек внутренних преобразований.

“Векторное поле” f определение динамической системы должно быть представлено процедурой двумя входными параметрами: скалярное время t и матричный или векторный Y. Внутренне, f вызван действительными значениями с плавающей точкой t и матрицами/векторами Y того же доменного типа как начальное условие Y ₀.

Процедура f должен возвратить n ×n матрица любой как array(1..n, 1..n) или как соответствующий матричный объект категории Cat::Matrix (сгенерированный функциональным matrix).

Рекомендуется, чтобы процедура возвратила массив типа array(1..n, 1..n). Это избегает издержек внутренних преобразований.

Возвращаемое значение f может содержать числовые выражения, такие как π, и т.д. Однако все значения должны быть конвертируемыми к действительным или комплексным числам с плавающей точкой float.

Автономные системы, где f (t, Y) не зависит от t, должны быть представлены процедурой с двумя аргументами t и Y, также.

Дополнительные аргументы method, RelativeError = tol, и Stepsize = h определите, как ОДУ решен. Они соответствуют методам классического решателя ОДУ numeric::odesolve.

Числовой точностью управляет глобальная переменная DIGITS: адаптивное управление размера шага сохраняет локальные относительные ошибки дискретизации ниже, если различный допуск не задан с помощью опции RelativeError = tol. Контроль ошибок может быть выключен путем определения фиксированного Stepsize = h.

Примечание

Только локальными ошибками управляет адаптивный механизм. Никакое управление глобальной ошибки не обеспечивается!

С Y := t -> numeric::odesolveGeometric(f, t_0..t, Y_0), числовое решение может быть repesented функцией MuPAD^®: вызов Y(t) запустит численное интегрирование с t ₀ к t.

Классическое интегрирование сохраняет геометрические инварианты до относительной точности решения, тогда как геометрический интегратор сохраняет инварианты, независимые от tol до рабочей точности, установленной DIGITS: отклонение от гомогенного коллектора является чистым эффектом округления.

numeric::odesolveGeometric полезно, когда допуск tol много largerthan задан RelativeError = tol. Для маленьких допусков можно рассмотреть, чтобы использовать классический решатель numeric::odesolve вместо этого.

Поскольку классическое интегрирование является значительно более быстрыми, большими значениями DIGITS и меньшие допуски к ошибке дискретизации могут использоваться в numeric::odesolve. В зависимости от конкретной проблемы это может привести к лучшим результатам, чем произведенный numeric::odesolveGeometric.

Взаимодействия среды

Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.

Примеры

Пример 1

Мы рассматриваем задачу с начальными значениями

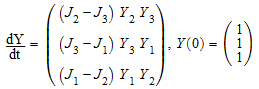
поскольку фиксированными параметрами, J ₂ = 1, J ₃ = 2. Запись этого ОДУ как

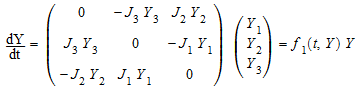ясно, что решение ограничивается орбитой ортогональной группы SO (3) через начальную точку (f ₁ производит скошенные симметричные матрицы). Инвариант этого действия, т.е. решение ограничивается сферой. Запись ОДУ как

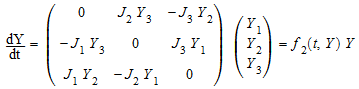
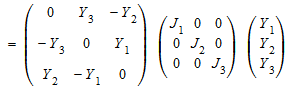ясно, что решение также ограничивается орбитой группы “J-orthogonal” SO (J, 3) через начальную точку. Эта группа состоит из матриц G, удовлетворяющий G ^T J G = J, где J = diag (J ₁, J ₂, J ₃). Инвариант этих действий группы, т.е. решение ограничивается эллипсоидом.

Мы рассматриваем первое представление и вычисляем числовое решение, которое ограничивается сферой:

f1 := proc(t, Y) begin 
      array(1..3, 1..3, [ [   0    , -J3*Y[3],  J2*Y[2]],
                          [ J3*Y[3],    0    , -J1*Y[1]],
                          [-J2*Y[2],  J1*Y[1],    0    ]])
end_proc:
J1 := 1/2: J2 := 1: J3 := 2: 
tol := 10^(-2):
Gsolve:= (f, t0_t, Y0) -> 
  numeric::odesolveGeometric(f, t0_t, Y0, RelativeError = tol):

Y(0) := [1.0, 1.0, 1.0];
Y(1) := Gsolve(f1, 0..1, Y(0));
Y(2) := Gsolve(f1, 1..2, Y(1));
Y(3) := Gsolve(f1, 2..3, Y(2));
Y(4) := Gsolve(f1, 3..4, Y(3));
Y(5) := Gsolve(f1, 4..5, Y(4))

Инвариантный H ₁ сохраняется численно до рабочей точности, установленной DIGITS:

H1 := Y -> Y[1]^2 + Y[2]^2 + Y[3]^2:
H1(Y(i)) - H1(Y(0)) $ i = 1..5

Инвариантный H ₂ только сохраняется в относительной точности решения, установленного опцией RelativeError = tol:

H2 := Y -> J1*Y[1]^2 + J2*Y[2]^2 + J3*Y[3]^2:
H2(Y(i)) - H2(Y(0)) $ i = 1..5

Теперь мы решаем ОДУ с помощью второго представления:

f2 := proc(t, Y) begin 
      array(1..3, 1..3, [ [   0    ,  J2*Y[3], -J3*Y[2]],
                          [-J1*Y[3],    0    ,  J3*Y[1]],
                          [ J1*Y[2], -J2*Y[1],    0    ]])
end_proc:

Y(0) := [1.0, 1.0, 1.0];
Y(1) := Gsolve(f2, 0..1, Y(0));
Y(2) := Gsolve(f2, 1..2, Y(1));
Y(3) := Gsolve(f2, 2..3, Y(2));
Y(4) := Gsolve(f2, 3..4, Y(3));
Y(5) := Gsolve(f2, 4..5, Y(4))

Теперь инвариантный H ₂ сохраняется к рабочей точности, пока H ₁ только сохраняется к допуску, заданному RelativeError = tol:

H2(Y(i)) - H2(Y(0)) $ i = 1..5

H1(Y(i)) - H1(Y(0)) $ i = 1..5

delete J1, J2, J3, Gsolve, f1, f2, Y, H1, H2:

Пример 2

Мы рассматриваем “Уравнения решетки Toda”

с a ₀ = a _n = 0. Представление трехдиагонального n ×n матрицы

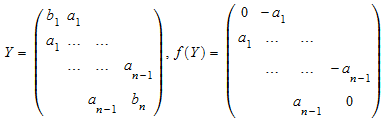эти уравнения могут быть закодированы матричным ОДУ. Решение Y (t), как известно, является “изоспектральным”, т.е. собственные значения Y (t), не зависит от параметра времени t. Как упомянуто в описании опции LieGroupAction, решение этого типа матричного ОДУ дано действиями группы Y (t) = G (t) Y (0) G (t) ^{- 1} = G (t) Y (0) G (t) ^T, где G (t) является ортогональными матрицами (обратите внимание, что f (Y) является симметричным скосом). Собственные значения матриц Y (t) являются инвариантами действий группы.

Точная динамика также сохраняет трехдиагональную форму матриц. Числовая динамика, однако, заполняет дальнейшие элементы. Следующее векторное поле f игнорирует alle элементы вне центральных полос:

f := proc(t, Y) 
local i, r;
begin
  r := array(1..n, 1..n, [[0 $ n] $ n]);
  for i from 1 to n - 1 do
    r[i + 1, i] :=  Y[i, i + 1];
    r[i, i + 1] := -Y[i, i + 1];
  end_for;
  return(r)
end_proc:

В следующем начальное значение Y (0) задан матрицей, сгенерированной функциональным matrix. Следовательно, оба аргумента G и Y передаются действию группы Ли LAMBDA как соответствующие матрицы. Они могут быть умножены на оператор умножения *:

LAMBDA:= proc(G, Y)
begin
  G*Y*(G::dom::transpose(G))
end_proc:

Мы задаем начальное значение:

n := 3:
Y(0) := matrix(n, n, [1, 1, 1], Banded)

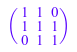
Теперь динамика интегрирована от t = 0 к t = 1:

tol := 10^(-4):
Y(1) := numeric::odesolveGeometric(f, 0..1, Y(0),
        LieGroupAction = LAMBDA, RelativeError = tol)

Инварианты динамики являются собственными значениями матриц Y (t). Они сохраняются численно:

numeric::eigenvalues(Y(0)) = numeric::eigenvalues(Y(1))

Для сравнения мы также решаем уравнения решетки Toda классическими численными данными с помощью numeric::odesolve. Система закодирована векторным Y = [b ₁, …, b _n, a ₁, …, a _{n - 1}] в:

f := proc(t, Y) 
local a, b, i;
begin
  b := [Y[i] $ i = 1..n];
  a := [Y[n + i] $ i = 1..n-1];
  [-2*a[1]^2,                           // = d/dt b[1]
    2*(a[i-1]^2 - a[i]^2) $ i = 2..n-1, // = d/dt b[i]
    2*a[n-1]^2,                         // = d/dt b[n]
    a[i]*(b[i] - b[i+1]) $ i = 1..n-1   // = d/dt a[i]
  ]
end_proc:

solution := numeric::odesolve(f, 0..1, [1 $ 2*n - 1],
                              RelativeError = tol);

Инварианты только сохраняются с точностью решения, определенного набором допуска через RelativeError = tol:

Y(1) := array(1..n, 1..n, [[0 $ n] $ n]):
for i from 1 to n do
  Y(1)[i, i] := solution[i];
end_for:
for i from 1 to n-1 do
  Y(1)[i, i + 1] := solution[n + i];
  Y(1)[i + 1, i] := solution[n + i];
end_for:

Y(1)

numeric::eigenvalues(Y(1))

Сравнивая эти данные с ранее вычисленными собственными значениями начального условия Y (0), каждый видит, что инварианты не сохраняются численно к рабочей точности, определенной DIGITS.

delete f, LAMBDA, n, Y, tol, solution, i:

Параметры

`f`	Процедура, принимающая два параметра `(t, Y)`
`_t0`	Числовое действительное значение в течение начального времени
`t`	Числовое действительное значение (“время”)
`_Y0`	Начальное условие: список, 1-мерный `array(1..n)`, 2-мерный `array(1..n, 1..m)`, или n ×m `matrix` из категории `Cat::Matrix` с числовыми записями

Опции

`LieGroupAction`	Опция, заданная как `LieGroupAction = LAMBDA` Процедура `LAMBDA = proc(G, Y) ... end_proc` задает действие элемента группы `G` (n ×n матрица) на точке Y на гомогенном коллекторе (n ×m матрица или n размерный вектор). Эта процедура должна возвратить соответствующую точку (матрица или вектор). Действие по умолчанию является обычным умножением матриц. При использовании этой опции, действия группы по умолчанию `LAMBDA`: из n ×n матрицы G, действующий на n ×m матрицы или n размерные векторы `Y` левым умножением может быть заменен другими действиями группы. Как действия группы, процедура `LAMBDA` должен удовлетворить LAMBDA (1_{n, n}, Y) = Y и . `numeric::odesolveGeometric` вычисляет решение матричного ОДУ На пробеле n ×n матрицы и возвращает Y (t) = LAMBDA (G (t), Y ₀). Для стандартных действий группы LAMBDA (G, Y) = G Y, это - решение ОДУ. Для гомогенных коллекторов, встроенных в n ×n матрицы, действия группы LAMBDA (G, Y) = может быть рассмотрен G YG-1. Для этого действия, кривая Y (t) = LAMBDA (G (t), Y ₀) возвращенный `numeric::odesolveGeometric` решение ОДУ. См. Пример 2. `LAMBDA(G, Y)` вызван n ×m матрицами или n размерными векторами `Y` из того же доменного типа как начальное условие Y ₀. Если Y ₀ является матрицей, сгенерированной функциональным `matrix`, затем также n ×n матричный G передается `LAMBDA` как таковой матричный объект. Во всех других случаях G передается как 2-мерный `array(1..n, 1..n)`. Процедура `LAMBDA` должен возвратить 2-мерный `array(1..n, 1..m)` или соответствующая матрица категории `Cat::Matrix`. Если начальное условие Y ₀ задано списком или 1-мерным `array(1..n)\lambda` май также возвращает соответствующий список или массив. Внутренне, возвращаемое значение `LAMBDA` преобразован в 2-мерный `array(1..n, 1..m)` где m = 1, если список или 1-мерный массив возвращены. Этому рекомендуют тот `LAMBDA` возвращает 2-мерный `array(1..n, 1..m)` во избежание издержек внутренних преобразований.
`RelativeError`	Опция, заданная как `RelativeError = tol` Обеспечивает внутренние числовые шаги Рунге-Кутта, чтобы использовать размеры шага с локальными ошибками дискретизации ниже `tol`. Этот допуск должен быть числовым действительным значением. Допуск по умолчанию. Механизм внутреннего контроля оценивает локальную относительную ошибку дискретизации шага Рунге-Кутта и настраивает размер шага адаптивно, чтобы сохранить эту ошибку ниже `tol`. Настройка по умолчанию гарантирует, что локальные ошибки дискретизации имеют тот же порядок величины как числовое округление. Обычно нет никакой потребности использовать эту опцию, чтобы изменить эти настройки. Однако иногда численная оценка шагов Рунге-Кутта может быть плохо обусловлена или продвинуться, размеры так малы, что параметр времени не может быть постепенно увеличен размером шага в рабочей точности. В таком случае эта опция может использоваться к связанному локальная ошибка дискретизации tol и использовать более высокую рабочую точность, данную `DIGITS`. Только действительные численные значения приняты. Примечание Обычно, глобальная ошибка числового приближения, возвращенного `numeric::odesolveGeometric` больше, чем локальные ошибки, ограниченные `tol`. Несмотря на то, что результат отображен с `DIGITS` десятичные разряды, не нужно ожидать, что все они правильны. Относительной точностью конечного результата является `tol` в лучшем случае!
`Stepsize`	Опция, заданная как `Stepsize = h` Выключает внутренний контроль ошибок и использует итерацию Рунге-Кутта с постоянным размером шага `hH` должно быть числовое действительное значение. По умолчанию, `numeric::odesolveGeometric` использует адаптивный механизм управления размера шага в числовой итерации. Опция `Stepsize = h` выключает этот адаптивный механизм и использует Метод Рунге-Кутта, заданный `method` (или метод по умолчанию `DOPRI78`) с постоянным размером шага `h`. Последний шаг с меньшим размером шага используется, чтобы совпадать с концом t интервала интегрирования, если не целое число. Примечание При использовании этой опции нет никакого автоматического контроля ошибок! В зависимости от проблемы и на порядке метода, результатом может быть плохое числовое приближение точного решения. Обычно нет никакой потребности вызвать эту опцию. Однако иногда встроенный адаптивный механизм контроля ошибок может перестать работать при интеграции близко к сингулярности. В таком случае эта опция может использоваться, чтобы настроить механизм управления для глобальной ошибки при помощи различных размеров шага и исследования сходимости соответствующих результатов.
`Alldata`	Опция, заданная как `Alldata = n` При использовании этой опции, `numeric::odesolveGeometric` возвращает список числовых точек mesh [[t ₀, Y ₀], [t ₁, Y ₁], …, [t, Y (t)]] сгенерированный внутренней итерацией Рунге-Кутта. Целочисленный n управляет размером списка выходов. Для n = 1, возвращены все внутренние точки mesh. Этот случай может также быть вызван путем ввода упрощенной опции `Alldata`, который эквивалентен `Alldata = 1`. Для n> 1, только каждый n-th точка mesh хранится в списке. Список всегда содержит начальную точку [t ₀, Y ₀] и конечная точка [t, Y (t)]. Для n ≤ 0, только данные [[t ₀, Y ₀], [t, возвращен Y (t)]]. Список выходов может быть полезным, чтобы смотреть внутренний числовой процесс. Также дальнейшая графическая обработка данных о mesh может быть полезной.

Возвращаемые значения

Решение Y (t) возвращено как список или как массив значений с плавающей точкой. Тип матрицы/вектора результата совпадает с типом входной матрицы/вектора _Y0.

С опцией Alldata, список данных о mesh возвращен.

Ссылки

[1] Х. Манзэ-Каас и А. Зэнна: “Численное интегрирование дифференциальных уравнений на гомогенных коллекторах”, во Ф. Какере (редактор)., Основы Вычислительной Математики, Спрингер (1997), стр 305-315.

Документация

`numeric`::`odesolveGeometric`

Синтаксис

Описание

Примечание

Взаимодействия среды

Примеры

Пример 1

Пример 2

Параметры

Опции

Примечание

Примечание

Возвращаемые значения

Ссылки

Смотрите также

Функции MuPAD

MuPAD графические примитивы

Документация Symbolic Math Toolbox

Поддержка