numeric::odesolve2Числовое решение обыкновенного дифференциального уравнения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
numeric::odesolve2(f, t0, Y0, <method>, <RememberLast>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <MaxStepsize = hmax>)
numeric::odesolve2( f, t0, Y0, … ) возвращает функцию, представляющую числовое решение Y (t) дифференциального уравнения первого порядка (динамическая система)
, Y (t 0) = Y 0 с
и
.
Служебная функция numeric::ode2vectorfield может использоваться, чтобы произвести входные параметры f, t0, Y0 от набора дифференциальных выражений, представляющих ОДУ. См. Пример 1.
Функция сгенерирована Y := numeric::odesolve2(f, t0, Y0) по существу
Y := t -> numeric::odesolve(t_0..t, f, Y_0).
Численное интегрирование запускается, когда Y вызван действительным числовым аргументом. Вызов Y(t) возвращает вектор решения в формате, соответствующем типу начального условия Y 0 с который Y был задан: Y(t) или дает к списку или 1-мерному массиву.
Если t не действительное численное значение, затем Y(t) возвращает символьный вызов функции.
Смотрите страницу справки numeric::odesolve для получения дополнительной информации о параметрах и опциях.
Опции Alldata = n и Symbolic принятый numeric::odesolve не окажите влияние: numeric::odesolve2 игнорирует эти опции.
Без RememberLast, функциональный Y помнит все значения, которые он вычислил. При вызове Y (T) это ищет помнить таблицу в течение времени t0 < T < t, самый близкий к t, и объединяется от T до t с помощью ранее вычисленного Y (T) в качестве начального значения. Здесь, t0 является временем, в течение которого дано начальное значение ОДУ. Это уменьшает затраты на вызов значительно, если Y должен много раз оцениваться, например, при графическом выводе решения для ОДУ. Лучший подход должен вызвать Y только с монотонно увеличением (или уменьшение) последовательность значений t, начинающий с t0. Далее, функция должна быть повторно инициализирована каждый раз, когда DIGITS увеличен. Смотрите Пример 3.
Функция возвращена numeric::odesolve2 чувствительно к переменной окружения DIGITS, который определяет числовую рабочую точность.
Без RememberLast, функция возвращена numeric::odesolve2 использование option remember.
Числовое решение задачи с начальными значениями
, y (0) = 2 представлен следующим функциональным Y = [y]:
f := (t, Y) -> [t*sin(Y[1])]:
В качестве альтернативы служебная функция numeric::ode2vectorfield может использоваться, чтобы сгенерировать входные параметры более интуитивным способом:
[f, t0, Y0] :=
[numeric::ode2vectorfield({y'(t) = t*sin(y(t)), y(0) = 2}, [y(t)])]
Y := numeric::odesolve2(f, t0, Y0)
Процедура Y запускает численное интегрирование, когда названо числовым аргументом:
Y(-2), Y(0), Y(0.1), Y(PI + sqrt(2))
Вызов Y с символьным аргументом дает к символьному вызову:
Y(t), Y(t + 5), Y(t^2 - 4)
eval(subs(%, t = PI))
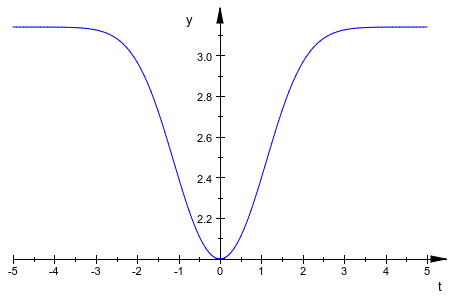
Числовое решение может быть построено. Обратите внимание на то, что Y(t) возвращает список, таким образом, мы строим элемент списка Y(t)[1]:
plotfunc2d(Y(t)[1], t = -5..5):
delete f, t0, Y0, Y:
Мы считаем дифференциальное уравнение
с начальными условиями y (0) = 0
. Уравнение второго порядка преобразовано в систему первого порядка для
:
.
f := (t, Y) -> [Y[2], Y[1]^2]: t0 := 0: Y0 := [0, 1]: Y := numeric::odesolve2(f, t0, Y0): Y(1), Y(PI)
delete f, t0, Y0, Y:
Мы рассматриваем систему
:
f := (t, Y) -> [Y[1] + Y[2], Y[1] - Y[2]]: Y := numeric::odesolve2(f, 0, [1, I]): DIGITS := 5: Y(1)
Увеличение DIGITS не приводит к более точному результату из-за помнить механизма:
DIGITS := 15: Y(1)
Это - предыдущее значение, вычисленное с 5 цифрами, распечатанными с 15 цифрами. Действительно, только 5 цифр правильны. Для получения результата, который является с точностью до полной точности, нужно стереть помнить таблицу через Y:=subsop(Y,5=NIL). В качестве альтернативы можно создать новое числовое решение с (пустым) новым, помнят таблицу:
Y := numeric::odesolve2(f, 0, [1, I]): Y(1)
delete f, Y, DIGITS:
Мы демонстрируем эффект опции RememberLast. Мы рассматриваем ОДУ
:
f := (t, Y) -> [-Y[1] + sin(t)]: Y := numeric::odesolve2(f, 0, [1]): Z := numeric::odesolve2(f, 0, [1], RememberLast):
После многих вызовов Y, помнить таблицу стал большим. В каждом вызове, ища помнить таблицу входные параметры близко к значению настоящего времени становится дорогим. Созданный с RememberLast, процедура Z не помнит всех его ранее вычисленных значений кроме последнего. Следовательно, это становится быстрее, чем Y:
time(for i from 1 to 1000 do Y(i/100) end)*msec, time(for i from 1 to 1000 do Z(i/100) end)*msec
Кроме КПД, значения, возвращенные Y и Z совпадите:
Y(10.5), Z(10.5)
delete f, Y, Z, i:
|
Процедура, представляющая векторное поле динамической системы |
|
Числовое действительное значение в течение начального времени |
|
Список или 1-мерный массив численных значений, представляющих начальное значение |
|
Одна из схем Runge-Kutta описана ниже. |
|
Опция, заданная как Имя схемы Runge-Kutta. Для получения дополнительной информации см. документацию |
|
Изменяет внутреннее, помнят механизм: процедура возвращена Без этой опции, процедуры, возвращенной Эта опция настоятельно рекомендована когда числовая процедура, возвращенная |
|
Опция, заданная как Обеспечивает внутренние числовые шаги Рунге-Кутта, чтобы использовать размеры шага с относительными локальными ошибками дискретизации ниже |
|
Опция, заданная как Обеспечивает внутренние числовые шаги Рунге-Кутта, чтобы использовать размеры шага с абсолютными локальными ошибками дискретизации ниже |
|
Опция, заданная как Выключает внутренний контроль ошибок и использует итерацию Рунге-Кутта с постоянным размером шага |
|
Опция, заданная как Ограничивает адаптивные размеры шага значениями, не больше, чем |
Процедура.
