`plot`::`Implicit2d`

Линии контура функции от R^2 до R

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

plot::Implicit2d(f, x = x_min .. x_max, y = y_min .. y_max, <a = a_min .. a_max>, options)

Описание

_{plot::Implicit2d(f(x, y), x = xmin..xmax , y = ymin..ymax )} строит кривые где сглаженный функциональный f нуль.

_{plot::Implicit2d(f, x = xmin..xmax , y = ymin..ymax )} строит обнуление f в данной области значений, т.е. набор.

plot::Implicit2d принимает, что f является регулярным почти везде на этой кривой, что означает, что f должен быть дифференцируемым, и по крайней мере одна из его частных производных должна быть ненулевой.

Построить другие контуры, чем обнуляет, используйте опцию Contours.

Атрибуты

Атрибут	Цель	Значение по умолчанию
`AffectViewingBox`	влияние объектов на `ViewingBox` из сцены	`TRUE`
`AntiAliased`	сглаженные линии и точки?	`TRUE`
`Color`	основной цвет	`RGB::Blue`
`Contours`	контуры неявной функции	[0]
`Frames`	количество систем координат в анимации	50
`Function`	выражение function или процедура
`Legend`	делает запись легенды
`LegendText`	короткий объяснительный текст для легенды
`LegendEntry`	добавить этот объект в легенду?	`TRUE`
`LineColor`	цвет линий	`RGB::Blue`
`LineWidth`	ширина линий	0.35
`LineColor2`	цвет линий	`RGB::DeepPink`
`LineStyle`	тело, подчеркнутые штриховой линией или пунктирные линии?	`Solid`
`LinesVisible`	видимость линий	`TRUE`
`LineColorType`	типы окраски линии	`Flat`
`LineColorFunction`	функциональная окраска линии
`LineColorDirection`	направление цветовых переходов на линиях	[0, 1]
`LineColorDirectionX`	x-компонент направления цветовых переходов на линиях	0
`LineColorDirectionY`	y-компонент направления цветовых переходов на линиях	1
`Mesh`	количество точек выборки	[11, 11]
`Name`	имя объекта графика (для браузера и легенды)
`ParameterEnd`	закончите значение параметра анимации
`ParameterName`	имя параметра анимации
`ParameterBegin`	начальное значение параметра анимации
`ParameterRange`	область значений параметра анимации
`TimeEnd`	время окончания анимации	10.0
`TimeBegin`	время начала анимации	0.0
`TimeRange`	оперативный промежуток анимации	0.0.. 10.0
`Title`	объектный заголовок
`TitleFont`	шрифт объектных заголовков	[`" sans-serif "`, 11]
`TitlePosition`	положение объектных заголовков
`TitleAlignment`	выравнивание по горизонтали заголовков w.r.t. их координаты	`Center`
`TitlePositionX`	положение объектных заголовков, x компонент
`TitlePositionY`	положение объектных заголовков, y компонент
`Visible`	видимость	`TRUE`
`VisibleAfter`	объект, видимый после этой временной стоимости
`VisibleBefore`	объект, видимый до этой временной стоимости
`VisibleFromTo`	объект, видимый в это время, располагается
`VisibleAfterEnd`	объект, видимый после его законченного времени анимации?	`TRUE`
`VisibleBeforeBegin`	объект, видимый перед его временем анимации, запускается?	`TRUE`
`XMax`	окончательное значение параметра “x”
`XMesh`	количество точек выборки для параметра “x”	11
`XMin`	начальное значение параметра “x”
`XName`	имя параметра “x”
`XRange`	область значений параметра “x”
`YMax`	окончательное значение параметра “y”
`YMesh`	количество точек выборки для параметра “y”	11
`YMin`	начальное значение параметра “y”
`YName`	имя параметра “y”
`YRange`	область значений параметра “y”

Примеры

Пример 1

Это известно, что круг может быть описан как:

plot(plot::Implicit2d(x^2+y^2-1, x = -1..1, y = -1..1))

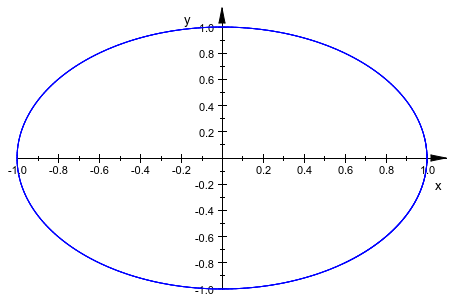
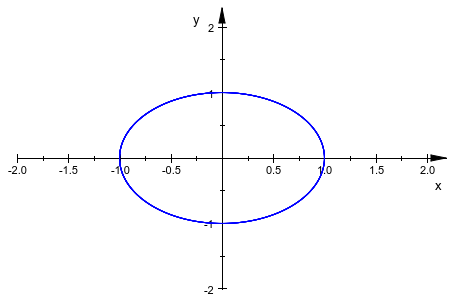
Обратите внимание на то, что plot::Implicit2d использует данную область значений полностью, даже если нет ничего, чтобы построить на границе:

plot(plot::Implicit2d(x^2+y^2-1, x = -2..2, y = -2..2))

Пример 2

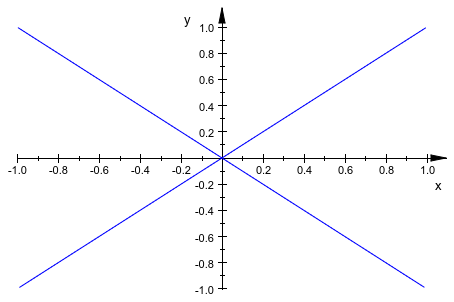
plot::Implicit2d функции указателей, которые не являются регулярными в изолированных точках на контурах:

plot(plot::Implicit2d((x-y)*(x+y), x = -1..1, y = -1..1))

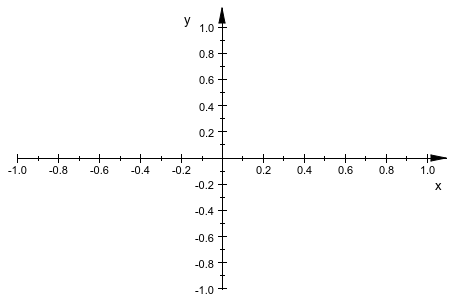
Однако это перестало работать, если функция сингулярна на больше, чем изолированных точках:

plot(plot::Implicit2d(0, x = -1..1, y = -1..1))

Пример 3

Мы строим некоторые эллиптические кривые y ² = x ³ + 4 x + c:

plot(plot::Implicit2d(y^2 - x^3 + 4*x, x = -3..3, y = -4..4, 
                      Contours = [c $ c = -3..6]))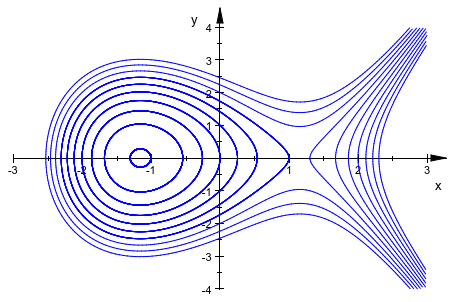

Пример 4

Как большинство графических объектов, plot::Implicit2d может быть анимирован легко:

plot(plot::Implicit2d(x^2 - y^2 = (x - a*y)*(x^2 + y^2),
                      x = -2..2, y = -2..2, a = -2..2))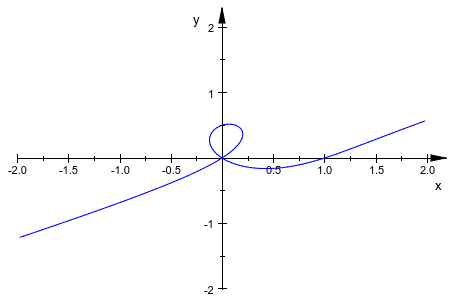

Параметры

`f`	Выражение с действительным знаком или уравнение в `xY`, и возможно параметр анимации. `f` эквивалентно атрибуту `Function`.
`xY`	идентификаторы. `xY` эквивалентны атрибутам `XName`, `YName`.
`_{xmin .. xmax}`, `_{ymin .. ymax}`	Выражения с действительным знаком, возможно в параметре анимации. Изображение построено с `x` в области значений _xmin ≤ x ≤ _xmax и _ymin ≤ y ≤ _ymax. `_xmin` `_xmax_ymin` `_ymax` эквивалентны атрибутам `XRangexmin` `xmax` `YRange` `ymin` `ymax` .
`a`	Параметр анимации, заданный как `a` `_{= amin..amax}`, где `_amin` начальное значение параметров и `_amax` итоговое значение параметров.

Алгоритмы

plot::Implicit2d использует метод отслеживания кривой: Это сначала генерирует начальные точки на кривой и затем использует метод прогноза и коррекции, чтобы следовать за кривой, таким образом найденной в обоих направлениях, с помощью теоремы неявной функции.

Документация

`plot`::`Implicit2d`

Синтаксис

Описание

Атрибуты

Примеры

Пример 1

Пример 2

Пример 3

Пример 4

Параметры

Алгоритмы

Смотрите также

Функции MuPAD

MuPAD графические примитивы

Документация Symbolic Math Toolbox

Поддержка