simplifyRadicalУпростите радикалов в арифметических выражениях
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
simplifyRadical(z)
simplifyRadical(z) попытки упростить радикалов в выражении z. Результат математически эквивалентен z.
radsimp и simplifyRadical эквивалентны.
Упростите эти константные выражения с радикалами высшего порядка и квадратными корнями:
simplifyRadical(3*sqrt(7)/(sqrt(7) - 2)), simplifyRadical(sqrt(5 + 2*sqrt(6))); simplifyRadical(sqrt(5*sqrt(3) + 6*sqrt(2))), simplifyRadical(sqrt(3 + 2*sqrt(2)))
![]()
![]()
simplifyRadical((1/2 + 1/4*3^(1/2))^(1/2))
![]()
simplifyRadical((5^(1/3) - 4^(1/3))^(1/2))
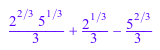
simplifyRadical(sqrt(3*sqrt(3 + 2*sqrt(5 - 12*sqrt(3 - 2*sqrt(2))))
+ 14))![]()
simplifyRadical(2*2^(1/4) + 2^(3/4) - (6*2^(1/2) + 8)^(1/2))
![]()
simplifyRadical(sqrt(1 + sqrt(3)) + sqrt(3 + 3*sqrt(3))
- sqrt(10 + 6*sqrt(3)))![]()
Создайте следующее выражение и затем упростите его с помощью simplifyRadical:
x := sqrt(3)*I/2 + 1/2: y := x^(1/3) + x^(-1/3): z := y^3 - 3*y
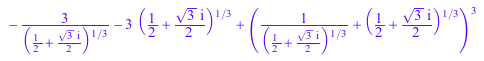
simplifyRadical(z)
![]()
delete x, y, z:
Используйте simplifyRadical упростить эти арифметические выражения содержащие переменные:
z := x/(sqrt(3) - 1) - x/2
![]()
simplifyRadical(z) = expand(radsimp(z))
![]()
delete z:
Используйте simplifyRadical упростить вложенных радикалов. Когда упрощение вложило радикалов, simplifyRadical попытки уменьшать глубину вложения:
simplifyRadical((6*2^(1/2) + 8)^(1/2)); simplifyRadical(((32/5)^(1/5) - (27/5)^(1/5))^(1/3)); simplifyRadical(sqrt((3+2^(1/3))^(1/2) * (4-2^(1/3))^(1/2)))
![]()
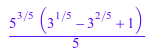
![]()
|
Арифметическое выражение.
Для постоянных алгебраических выражений, simplifyRadical создает башню из алгебраических расширений ℚ с помощью доменного Dom::AlgebraicExtension. Это пытается возвратить самую простую форму.
Эта функция основана на алгоритме, описанном в Бородине, Fagin, Hopcroft и Tompa, “Уменьшая Глубину вложения Выражений, Включающих Квадратные корни”, JSC 1, 1985, стр 169-188. В некоторых особых случаях, алгоритме на основе Ландау”, Как ругаться с вложенным радикалом”, Математический Тайный агент 16, 1994, № 2, стр 49-55, используется.