Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Большинство математических выражений может быть представлено в различных, но математически эквивалентных формах. Некоторые из этих форм могут выглядеть более простыми, например, они могут быть явно короче. Однако вы можете предпочесть другие формы того же выражения для числовых расчетов. Нет никакого общего правила, относительно которого форма выражения является самой простой. При решении конкретной задачи можно выбрать самую простую форму выражения для этой проблемы.
Помимо общего упрощения функционирует simplify и Simplify, MuPAD® обеспечивает набор функций для преобразования математических выражений к конкретным формам. Следующая таблица помогает вам выбрать функцию для преобразования вашего выражения к соответствующей форме. Чтобы видеть краткое описание функции и набор примеров, щелкните по ссылке в левом столбце. Чтобы видеть подробную страницу справки для функции, кликните по имени функции в правом столбце.
Если математическое выражение содержит условия с теми же степенями заданной переменной или выражения, collect функция реорганизовывает выражение, группирующее такие условия. При вызове collect, задайте переменные или выражения, которые функция должна рассмотреть как неизвестные. collect функционируйте рассматривает исходное выражение как полином в заданных неизвестных и группирует коэффициенты с равными степенями:
collect(x*y^4 + x*z + 2*x^3 + x^2*y*z + 3*x^3*y^4*z^2
+ y*z^2 + 5*x*y*z, x)![]()
collect может рассмотреть выражение как заданное неизвестное. Например, сгруппируйте условия следующего тригонометрического выражения с равными степенями sin(x) и cos(x):
f := cos(x)^4*sin(x) + cos(x)^2*sin(x)^3
+ cos(x)^2*sin(x)^2 - sin(x)^4:
collect(f, sin(x))![]()
collect(f, cos(x))
![]()
collect функция также может принять несколько неизвестных для сбора условий. Если вы имеете несколько неизвестных, передаете их collect как список:
collect(a^2*sin(x) - cos(x)^2*sin(x)^3 + cos(x)^2
+ a - a^2*sin(x)^4, [a, cos(x)])![]()
MuPAD также обеспечивает функцию для объединения подвыражений исходного выражения. combine функционируйте использует математические тождества в функциях, на которые вы указываете. Например, объедините тригонометрическое выражение:
combine(2*sin(x)*cos(x), sincos)
![]()
Если вы не задаете целевую функцию, combine использует тождества в степенях везде, где эти тождества допустимы:
a b ac = a b + c
a c bc = (a b) c, если c целое число
(a b) c = a bc, если c целое число
Например, по умолчанию функция комбинирует следующие квадратные корни:
combine(sqrt(2)*sqrt(x))
![]()
Функция не комбинирует эти квадратные корни, потому что идентичность не допустима для отрицательных величин переменных:
combine(sqrt(x)*sqrt(y))
![]()
Чтобы объединить эти квадратные корни, используйте IgnoreAnalyticConstraints опция:
combine(sqrt(x)*sqrt(y), IgnoreAnalyticConstraints)
![]()
Как целевые функции, combine принимает arctanexp\Gamma, ln, sincos, и другие функции. Для полного списка целевых функций смотрите combine страница справки.
Для элементарных выражений, expand функционируйте преобразовывает исходное выражение путем умножения сумм продуктов:
expand((x + 1)*(x + 2)*(x + 3))
![]()
expand также использует математические тождества между функциями:
expand(sin(5*x))
![]()
expand работает рекурсивно на все подвыражения:
expand((sin(3*x) + 1)*(cos(2*x) - 1))
![]()
Чтобы предотвратить расширение конкретных подвыражений, передайте эти подвыражения expand в качестве аргументов:
expand((sin(3*x) + 1)*(cos(2*x) - 1), sin(3*x))
![]()
Чтобы предотвратить расширение всех тригонометрических подвыражений в этом примере, используйте опцию ArithmeticOnly:
expand((sin(3*x) + 1)*(cos(2*x) - 1), ArithmeticOnly)
![]()
Чтобы представить выражение как продукт сумм, попробуйте factor функция. Учтенная форма следующего полинома явно короче, чем исходный. Учтенная форма также показывает, что этот полином имеет только один корневой x = -5:
factor(x^10 + 50*x^9 + 1125*x^8 + 15000*x^7 + 131250*x^6
+ 787500*x^5 + 3281250*x^4 + 9375000*x^3
+ 17578125*x^2 + 19531250*x + 9765625)![]()
За суммы рациональных выражений, factor сначала вычисляет общий знаменатель, и затем факторы и числитель и знаменатель:
f := (x^3 + 3*y^2)/(x^2 - y^2) + 3: f = factor(f)
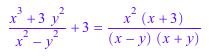
Функция также может учесть выражения кроме полиномов и рациональных функций. Внутренне, MuPAD преобразует такие выражения в полиномы или рациональную функцию путем замены подвыражениями с идентификаторами. После факторинга выражения с временными идентификаторами MuPAD восстанавливает исходные подвыражения:
factor((ln(x)^2 - 1)/(cos(x)^2 - sin(x)^2))
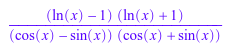
По умолчанию, factor поиски полиномиальных факторов с рациональными числами. Функция не включает выражение в продукт, содержащий![]() :
:
factor(x^2 - 2)
![]()
Чтобы добавить константу![]() в числа, используемые в факторинге, используйте опцию
в числа, используемые в факторинге, используйте опцию Adjoin:
factor(x^2 - 2, Adjoin = [sqrt(2)])
![]()
normal функция представляет исходное рациональное выражение как один рациональный термин с расширенным числителем и знаменателем. Наибольший общий делитель числителя и знаменатель возвращенного выражения равняются 1:
f := (x^3 + 3*y^2)/(x^2 - y^2) + 3: f = normal(f)
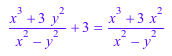
normal общие множители отмен, которые появляются в числителе и знаменателе:
f := x^2/(x + y) - y^2/(x + y): f = normal(f)
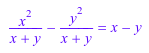
normal функционируйте также обрабатывает выражения кроме полиномов и рациональных функций. Внутренне, MuPAD преобразует такие выражения в полиномы или рациональные функции путем замены подвыражениями с идентификаторами. После нормализации выражения с временными идентификаторами MuPAD восстанавливает исходные подвыражения:
f := (exp(2*x) - exp(2*y))/(exp(3*x) - exp(3*y)): f = normal(f)
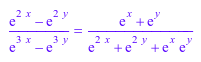
partfrac функция возвращает рациональное выражение в форме суммы полинома и рациональных условий. В каждом рациональном термине степень числителя меньше, чем степень знаменателя. Для некоторых выражений, partfrac возвращает явно более простые формы, например:
partfrac((x^6 + 15*x^5 + 94*x^4 + 316*x^3 + 599*x^2
+ 602*x + 247)/(x^6 + 14*x^5 + 80*x^4
+ 238*x^3 + 387*x^2 + 324*x + 108), x)![]()
Знаменатели в рациональных терминах представляют учтенный общий знаменатель исходного выражения:
factor(x^6 + 14*x^5 + 80*x^4 + 238*x^3 + 387*x^2 + 324*x + 108)
![]()
Как альтернатива общему simplifiers simplify и Simplify, используйте radsimp функция, чтобы упростить арифметические выражения, включающие квадратные корни или других радикалов. Например, упростите следующее числовое выражение:
f := 3*sqrt(7)/(sqrt(7) - 2); radsimp(f)
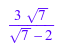
![]()
При работе с комплексными числами вы можете должны быть разделить действительную и мнимую часть символьного выражения. Чтобы извлечь действительную и мнимую часть комплексного числа, вы используете Re и Im функции. Для символьных выражений возвращаются эти функции:
Re(tan(x)), Im(tan(x))
![]()
Используйте rectform функционируйте, чтобы разделить символьное выражение в его действительные и мнимые части:
y := rectform(tan(x))
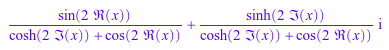
Извлекать действительные и мнимые части y, используйте Re и Im функции:
Re(y); Im(y)
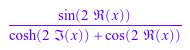
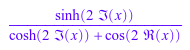
Чтобы представить выражение в терминах конкретной функции, используйте rewrite команда. Команда использует математические тождества между функциями. Например, перепишите выражение, содержащее тригонометрические функции в терминах конкретной тригонометрической функции:
sin(x) = rewrite(sin(x), tan); cos(x) = rewrite(cos(x), tan); sin(2*x) + cos(3*x)^2 = rewrite(sin(2*x) + cos(3*x)^2, tan)
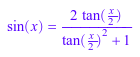
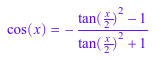
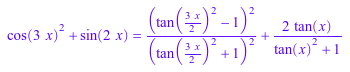
Используйте rewrite выражать тригонометрические и гиперболические функции в терминах показательной функции:
sin(x) = rewrite(sin(x), exp); cos(x) = rewrite(cos(x), exp); sinh(x) = rewrite(sinh(x), exp); cosh(x) = rewrite(cosh(x), exp)
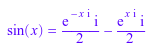
![]()
![]()
![]()
Команда также выражает обратные гиперболические функции в терминах логарифмов:
arcsinh(x) = rewrite(arcsinh(x), ln); arccosh(x) = rewrite(arccosh(x), ln)
![]()
![]()
Как целевые функции, rewrite принимает: прямые и обратные тригонометрические функции, прямые и обратные гиперболические функции, diffDerfexp, fact\Gamma, harmonic, piecewiseИ т.д. Смотрите rewrite страница справки для полного списка целевых функций.