`stats`::`correlation`

Корреляция между выборками данных

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

stats::correlation([x₁, x₂, …], [y₁, y₂, …], <BravaisPearson | Fechner>)
stats::correlation([[x₁, y₁], [x₂, y₂], …], <BravaisPearson | Fechner>)
stats::correlation(s, <c₁, c₂>, <BravaisPearson | Fechner>)
stats::correlation(s, <[c₁, c₂]>, <BravaisPearson | Fechner>)
stats::correlation(s₁, <c₁>, s₂, <c₂>, <BravaisPearson | Fechner>)

Описание

_{stats::correlation([x1, x2, …], [y1, y2, …])} возвращает линейное (Браве-Пирсон) коэффициент корреляции

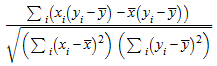где и средние значения данных x _i и y _i.

_{stats::correlation([x1, x2, …], [y1, y2, …], Fechner)} возвращает корреляцию Fechner, где n является объемом выборки. Номер v _i равняется 1, если и имеют тот же знак или оба 0. Это, если или или 0. В противном случае, v _i = 0.

И корреляция Браве-Пирсона, а также корреляция Fechner является числами между - 1 и 1.

Корреляция Браве-Пирсона близко к 1, если пары данных x _i, y _i приблизительно связан 'положительным' линейным отношением (т.е. y _i ≈ a x_i + b с некоторым положительным коэффициентом a). Это близко к - 1, если существует 'отрицательное' линейное отношение (с некоторым отрицательным коэффициентом a).

Коэффициенты корреляции близко к 0 соответствуют нелинейным отношениям или к несвязанным данным, соответственно.

Если входные данные являются числами с плавающей запятой, суммы, задающие корреляцию Браве-Пирсона, вычисляются численно устойчивым способом. Если результат с плавающей точкой желаем, рекомендуется убедиться, что все входные данные являются плаваниями.

Корреляция Fechner всегда возвращается как рациональное число.

Индексы столбца _c1_C2 являются дополнительными, если данные даны stats::sample объекты содержа только два столбца данных нестроки. Если данные обеспечиваются двумя выборками _s1_S2, индексы столбца являются дополнительными для выборок, содержащих только один столбец данных нестроки.

Примечание

Корреляция Fechner не должна быть вычислена для символьных данных. Это может привести к неожиданным результатам, если знак символьных параметров не может быть определен.

Внешние статистические данные, сохраненные в ASCII-файле, могут быть импортированы в сеанс MuPAD^® через import::readdata. В частности, смотрите Пример 1 из соответствующей страницы справки.

Примеры

Пример 1

Мы вычисляем корреляцию выборок, переданных как списки:

X := [7, 33/7, 3, 5, 2]: Y := [3, 5, 1, 7, 2]:
stats::correlation(X, Y)

В качестве альтернативы данные могут быть переданы как список пар данных:

stats::correlation([[7, 3], [33/7, 5], [3, 1], [5, 7], [2, 2]])

Если все данные являются числами с плавающей запятой, результатом является плавание:

stats::correlation(float(X), float(Y))

Корреляция Fechner данных всегда возвращается как рациональное число:

stats::correlation(X, Y, Fechner),
stats::correlation(float(X), float(Y), Fechner)

Следующий точный результат показывает на точное линейное между парами данных:

stats::correlation([0, 1, 2, 3], [7, 5, 3, 1])

Действительно, существует 'отрицательное' линейное отношение y = 7 - 2 x между парами данных.

delete X, Y:

Пример 2

Мы создаем выборку типа stats::sample:

s := stats::sample([[1.0, 2.4, 3.0], 
                    [7.0, 4.8, 4.0], 
                    [3.3, 3.0, 5.0]])

1.0  2.4  3.0
7.0  4.8  4.0
3.3  3.0  5.0

Мы вычисляем корреляцию между данными первого и третьим столбцом несколькими эквивалентными способами:

stats::correlation(s, 1, 3),
stats::correlation(s, [1, 3]),
stats::correlation(s, 1, s, 3)

stats::correlation(s, 1, 3, Fechner),
stats::correlation(s, [1, 3], Fechner),
stats::correlation(s, 1, s, 3, Fechner)

delete s:

Пример 3

С символьными данными корреляция Браве-Пирсона возвращена как символьное выражение:

stats::correlation([x1, x2], [y1, y2])

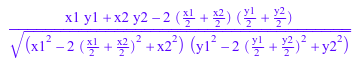
simplify(%)

Параметры

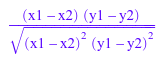
`_{x1, y1, x2, y2, …}`	Статистические данные: арифметические выражения. Количество данных x _i должно совпасть с количеством данных y _i.
`s_S1_S2`	Выборки статистики типа:: выборка
`_c1_C2`	Индексы столбца: положительные целые числа. Столбец `_c1` из `s` или `_s1`, соответственно, предоставляет данным x _i. Столбец `_c2` из `s` или `s_2`, соответственно, предоставляет данным y _i.
`mode`	Любой `BravaisPearson` или `Fechner`. Значением по умолчанию является линейное (Браве-Пирсон) корреляция.

Опции

BravaisPearson, Fechner

Линейный (Браве-Пирсон) или коэффициент корреляции Фекнера. Коэффициент Браве-Пирсона является значением по умолчанию, но может в некоторых случаях, где данные не нормально распределены быть менее полезными, чем корреляция Фекнера.

Возвращаемые значения

Корреляция Браве-Пирсона возвращена как арифметическое выражение. FAIL возвращен, если отклонение одной из выборок данных исчезает (корреляция Браве-Пирсона не существует).

Корреляция Fechner возвращена как рациональное число.

FAIL возвращен, если выборки данных пусты.

Смотрите также

Функции MuPAD

stats::correlationMatrix | stats::covariance | stats::stdev

MuPAD графические примитивы

plot::Scatterplot

Документация