stats::correlationMatrixВычислите корреляционную матрицу, сопоставленную с ковариационной матрицей
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
stats::correlationMatrix(cov)
stats::correlationMatrix(cov) возвращает в корреляционную матрицу cor из ковариационной матрицы отклонения cov. Этим дают:
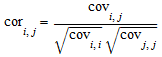 .
.
C ковариационной матрицы должен быть положительным (полу-) определенный и следовательно удовлетворяет |Cij|2 ≤ C ii Cjj для всех индексов i, j. Следовательно, абсолютные значения записей соответствующей корреляционной матрицы не превышают 1.
С опцией CovarianceMatrix, стандартный stats::reg возвращает ковариационную матрицу отклонения подходящих параметров в регрессионном анализе. Соответствующая корреляционная матрица подходящих параметров вычисляется удобно путем применения stats::correlationMatrix к этой матрице. См. Пример 2.
Мы генерируем положительную определенную матрицу, которая может служить ковариационной матрицей:
A := matrix([[4, -3, 2], [-1, 2, 1], [0, 1, 1]]): cov := A*linalg::transpose(A)

Соответствующая корреляционная матрица:
stats::correlationMatrix(cov)
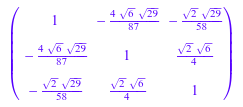
Если входная матрица состоит из данных с плавающей точкой, результатом является матрица плаваний:
stats::correlationMatrix(float(cov))

delete A, cov:
Мы рассматриваем ковариационную матрицу, возникающую в нелинейной проблеме регрессии. Функциональный y модели = a + b cos (x - c) должен быть подходящим к следующим рандомизированным данным:
r := stats::uniformRandom(-0.1, 0.1): xdata := [i $i = 1..100]: ydata := [1 + 2*cos(x - 3) + r() $ x in xdata]:
Конструкцией отклонение значений y является отклонением равномерно распределенных случайных данных по интервалу [-0.1, 0.1] сгенерированный случайным генератором r. Это отклонение![]() . Мы используем
. Мы используем stats::reg получить оценки подходящих параметров a, b, c модели. Соответствующими весами для регрессии дают![]() . Опция
. Опция CovarianceMatrix делает stats::reg включайте ковариационную матрицу cov из подходящих параметров в его списке возвратов:
weights := [300 $ i = 1..100]:
DIGITS:= 4:
[abc, chisquare, cov] :=
stats::reg(xdata, ydata, weights, a + b*cos(x - c),
[x], [a, b, c], StartingValues = [1, 2, 3],
CovarianceMatrix)
Корреляционная матрица параметров a, b, c получен через stats::correlationMatrix примененный ковариационная матрица cov возвращенный stats::reg:
stats::correlationMatrix(cov)

delete r, xdata, ydata, weights, DIGITS, abc, chisquare, cov:
|
Ковариационная матрица: квадратная матрица категории |
Матрица той же размерности и типа как входная матрица cov. FAIL возвращен если по крайней мере один из диагональных элементов входной матрицы cov нуль.