`whittakerM`

Функция Уиттекера М

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

whittakerM(a, b, z)

Описание

whittakerM возвращает функцию Уиттекера М, $M_{a, b} (z)$ .

Функции Уиттекера $M_{a, b} (z)$ и $W_{a, b} (z)$ линейно независимые решения следующего дифференциального уравнения:

$\frac{d^{2} w}{d z^{2}} + (- \frac{}{14} + \frac{a}{z} + \frac{\frac{}{14} - b^{2}}{z^{2}}) w = 0$

Функция Уиттекера М задана через вырожденную гипергеометрическую функцию $_{p} F_{q} (a, b, z) = Φ (a, b, z)$ можно следующим образом:

$M_{a, b} (z) = e^{- z / 2} z^{b + 1 / 2} Φ (b - a + \frac{}{12}, 1 + 2 b, z)$

Функция Уиттекера М задана для сложных аргументов aB, и z.

Для большинства значений параметров возвращен неоцененный вызов функции. Смотрите Пример 1.

Явные символьные выражения возвращены для некоторых особых значений параметров. Смотрите Пример 2.

Примечание

MuPAD^® задает ${}_{1}F_{1} (a, a, z) = e^{x}$ для всех комплексных чисел $a$ . Как следствие, MuPAD whittakerM функция отличается от соответствующей функции в М. Абрамовице и мне. А. Стегун, “Руководство Математических функций”, когда $b - a + \frac{}{12}$ и $1 + 2 b$ отрицательные целые числа и $b - a + \frac{}{12} \geq 1 + 2 b$ . Некоторые формулы в Главе 13 “Руководства Математических функций” не содержат для MuPAD whittakerM с такими аргументами. Смотрите Пример 4.

Взаимодействия среды

Когда названо аргументами с плавающей точкой, эти функции чувствительны к переменной окружения DIGITS который определяет числовую рабочую точность.

Примеры

Пример 1

Для точных или символьных аргументов, whittakerM отвечает на неоцененные звонки:

whittakerM(a, b, x);
whittakerM(-3/2, 1/2, 1)

Для аргументов с плавающей точкой, whittakerM возвращает результаты с плавающей точкой:

whittakerM(-2, 0.5, -50),
whittakerM(-3/2, 1/2, 1.0)

Пример 2

Для некоторых определенных значений параметров, whittakerM возвращает явные выражения:

whittakerM(0, b, x);
whittakerM(-3/2, 1/2, 0);
whittakerM(-3/2, 0, x)

Пример 3

diff, float, limit, series и другие функции обрабатывают выражения, включающие функцию Уиттекера М:

diff(whittakerM(a, b, z), z)

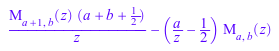
float(whittakerM(-3/2, 1/2, 1))

series(whittakerM(-3/2, 1/2, x), x)

Пример 4

Для некоторых значений входных параметров, повторения и дифференциальных отношений в Главе 13 М. Абрамовица и меня. А. Стегун, “Руководство Математических функций” не содержит для MuPAD whittakerM функции. Например, Формула 13.4.32

$z \frac{\partial}{\partial z} M_{a, b} (z) = (\frac{z}{2} - a) M_{a, b} (z) + (a + b + \frac{}{12}) M_{a + 1, b} (z)$

не удовлетворен для a = 0 и b = -3/2:

expand(x*diff(whittakerM(0, -3/2, x), x) <>
          x/2*whittakerM(0, -3/2, x) -
              whittakerM(1, -3/2, x))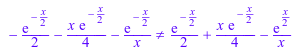

Параметры

aBZ

Арифметические выражения

Возвращаемые значения

Арифметическое выражение.

Перегруженный

z

Смотрите также

Функции MuPAD

hypergeom | kummerU | whittakerW

Документация